简单选择排序
算法介绍
在待排序序列中找到最小元素,存放到已排好序的有序表的终点位置,从而得到一个新的、记录数量增1的有序表。
算法例题
用随机函数生成16个2位正整数(10~99),利用 简单选择排序法 将其排序。
算法思路
书面概括
- 将待排序的元素存放在数组 r[1...n] 中。第一趟从 r[1] 开始,通过 n-1 次比较,从 n 个元素中选出关键字最小的元素,记为 r[k] ,交换 r[1] 和 r[k] ;
- 第二趟从 r[2] 开始,通过 n-2 次比较,从 n-1 个元素中选出关键字最小的元素,记为 r[k] ,交换 r[2] 和 r[k] ;
- 以此类推,第 i 趟从 r[i] 开始,通过 n-i 次比较,从 n-i 次比较,从 n-i+1 个元素中选出关键字最小的元素,记为 r[k] ,交换 r[i] 和 r[k] ;
- 经过 n-1 趟,排序完成。
个人概括
每趟排序都从 待排序序列 中选出一个 最小的元素 ,插入到 有序序列 的最后(其实是最小元素与待排序序列中第一个元素交换,交换后的最小的元素序列就是有序序列)。
考虑情况
-
每趟排序寻找最小元素时,先记录待排序元素的下标为暂记最小元素的索引
- 若比较完毕后,暂记最小元素的索引为待排序元素的下标,即待排序元素就是最小元素,无需移动,直接更新为有序序列;
- 若比较完毕后,暂记最小元素的索引不为待排序元素的下标,需要进行移动交换,再更新有序序列。
图解过程
( ) 为暂记最小元素,[ ] 为待排序序列,{ } 为有序序列,< > 为比较中的元素," " 为交换位置的元素。
1.第一趟排序
( ) [ 49 38 65 97 76 13 27 49 ]
更新暂记最小元素
( ) [<49> 38 65 97 76 13 27 49 ]
( 49 ) [(49) 38 65 97 76 13 27 49 ]
比较
( 49 ) [(49)<38> 65 97 76 13 27 49 ]
更新暂记最小元素
( ) [ 49 <38> 65 97 76 13 27 49 ]
( 38 ) [ 49 (38) 65 97 76 13 27 49 ]
比较
( 38 ) [ 49 (38)<65> 97 76 13 27 49 ]
( 38 ) [ 49 (38) 65 <97> 76 13 27 49 ]
( 38 ) [ 49 (38) 65 97 <76> 13 27 49 ]
( 38 ) [ 49 (38) 65 97 76 <13> 27 49 ]
更新暂记最小元素
( ) [ 49 38 65 97 76 <13> 27 49 ]
( 13 ) [ 49 38 65 97 76 (13) 27 49 ]
比较
( 13 ) [ 49 38 65 97 76 (13)<27> 49 ]
( 13 ) [ 49 38 65 97 76 (13) 27 <49>]
比较结束,将暂记最小元素与待排序序列第一个元素交换
( 13 ) ["49" 38 65 97 76 "13" 27 49 ]
( 13 ) ["13" 38 65 97 76 "49" 27 49 ]
更新待排序序列第一个元素为有序序列
( ) { 13 }[ 38 65 97 76 49 27 49 ]
2.第二趟排序
( ) { 13 }[ 38 65 97 76 49 27 49 ]
更新暂记最小元素
( ) { 13 }[<38> 65 97 76 49 27 49 ]
( 38 ) { 13 }[(38)<65> 97 76 49 27 49 ]
比较
( 38 ) { 13 }[(38) 65 <97> 76 49 27 49 ]
( 38 ) { 13 }[(38) 65 97 <76> 49 27 49 ]
( 38 ) { 13 }[(38) 65 97 76 <49> 27 49 ]
( 38 ) { 13 }[(38) 65 97 76 49 <27> 49 ]
更新暂最小记元素
( ) { 13 }[ 38 65 97 76 49 <27> 49 ]
( 27 ) { 13 }[ 38 65 97 76 49 (27) 49 ]
比较
( 27 ) { 13 }[ 38 65 97 76 49 (27)<49>]
比较结束,将暂记最小元素与待排序序列第一个元素交换
( 27 ) { 13 }["38" 65 97 76 49 "26" 49 ]
( 27 ) { 13 }["27" 65 97 76 49 "38" 49 ]
更新待排序序列第一个元素为有序序列
( ) { 13 27 }[ 65 97 76 49 38 49 ]
3.第三趟排序
( ) { 13 27 }[ 65 97 76 49 38 49 ]
更新暂记最小元素
( ) { 13 27 }[<65> 97 76 49 38 49 ]
( 65 ) { 13 27 }[(65) 97 76 49 38 49 ]
比较
( 65 ) { 13 27 }[(65)<97> 76 49 38 49 ]
( 65 ) { 13 27 }[(65) 97 <76> 49 38 49 ]
( 65 ) { 13 27 }[(65) 97 76 <49> 38 49 ]
更新暂最小记元素
( ) { 13 27 }[ 65 97 76 <49> 38 49 ]
( 49 ) { 13 27 }[ 65 97 76 (49) 38 49 ]
比较
( 49 ) { 13 27 }[ 65 97 76 (49)<38> 49 ]
更新暂最小记元素
( ) { 13 27 }[ 65 97 76 49 <38> 49 ]
( 38 ) { 13 27 }[ 65 97 76 49 (38) 49 ]
比较
( 38 ) { 13 27 }[ 65 97 76 49 (38)<49>]
比较结束,将暂记最小元素与待排序序列第一个元素交换
( 38 ) { 13 27 }["65" 97 76 49 "38" 49 ]
( 38 ) { 13 27 }["38" 97 76 49 "65" 49 ]
更新待排序序列第一个元素为有序序列
( ) { 13 27 38 }[ 97 76 49 65 49 ]
4.第四趟排序
( ) { 13 27 38 }[ 97 76 49 65 49 ]
更新暂记最小元素
( ) { 13 27 38 }[<97> 76 49 65 49 ]
( 97 ) { 13 27 38 }[(97) 76 49 65 49 ]
比较
( 97 ) { 13 27 38 }[(97)<76> 49 65 49 ]
更新暂记最小元素
( 97 ) { 13 27 38 }[ 97 <76> 49 65 49 ]
( 76 ) { 13 27 38 }[ 97 (76) 49 65 49 ]
比较
( 76 ) { 13 27 38 }[ 97 (76)<49> 65 49 ]
更新暂记最小元素
( 76 ) { 13 27 38 }[ 97 76 <49> 65 49 ]
( 49 ) { 13 27 38 }[ 97 76 (49) 65 49 ]
比较
( 49 ) { 13 27 38 }[ 97 76 (49)<65> 49 ]
( 49 ) { 13 27 38 }[ 97 76 (49) 65 <49>]
比较结束,将暂记最小元素与待排序序列第一个元素交换
( 49 ) { 13 27 38 }["97" 76 "49" 65 49 ]
( 49 ) { 13 27 38 }["49" 76 "97" 65 49 ]
更新待排序序列第一个元素为有序序列
( ) { 13 27 38 49 }[ 76 97 65 49 ]
5.第五趟排序
( ) { 13 27 38 49 }[ 76 97 65 49 ]
更新暂记最小元素
( ) { 13 27 38 49 }[<76> 97 65 49 ]
( 76 ) { 13 27 38 49 }[(76) 97 65 49 ]
比较
( 76 ) { 13 27 38 49 }[(76)<97> 65 49 ]
( 76 ) { 13 27 38 49 }[(76) 97 <65> 49 ]
更新暂记最小元素
( ) { 13 27 38 49 }[ 76 97 <65> 49 ]
( 65 ) { 13 27 38 49 }[ 76 97 (65) 49 ]
比较
( 65 ) { 13 27 38 49 }[ 76 97 (65)<49>]
更新暂记最小元素
( ) { 13 27 38 49 }[ 76 97 65 <49>]
( 49 ) { 13 27 38 49 }[ 76 97 65 (49)]
比较结束,将暂记最小元素与待排序序列第一个元素交换
( 49 ) { 13 27 38 49 }["76" 97 65 "49"]
( 49 ) { 13 27 38 49 }["49" 97 65 "76"]
更新待排序序列第一个元素为有序序列
( ) { 13 27 38 49 49 }[ 97 65 76 ]
6.第六趟排序
( ) { 13 27 38 49 49 }[ 97 65 76 ]
更新暂记最小元素
( ) { 13 27 38 49 49 }[<97> 65 76 ]
( 97 ) { 13 27 38 49 49 }[(97) 65 76 ]
比较
( 97 ) { 13 27 38 49 49 }[(97)<65> 76 ]
更新暂记最小元素
( ) { 13 27 38 49 49 }[ 97 <65> 76 ]
( 65 ) { 13 27 38 49 49 }[ 97 (65) 76 ]
比较
( 65 ) { 13 27 38 49 49 }[ 97 (65)<76>]
比较结束,将暂记最小元素与待排序序列第一个元素交换
( 65 ) { 13 27 38 49 49 }["97""65" 76 ]
( 65 ) { 13 27 38 49 49 }["65""97" 76 ]
更新待排序序列第一个元素为有序序列
( 65 ) { 13 27 38 49 49 65 }[ 97 76 ]
7.第七趟排序
( ) { 13 27 38 49 49 65 }[ 97 76 ]
更新暂记最小元素
( ) { 13 27 38 49 49 65 }[<97> 76 ]
( 97 ) { 13 27 38 49 49 65 }[(97) 76 ]
比较
( 97 ) { 13 27 38 49 49 65 }[(97)<76>]
更新暂记最小元素
( ) { 13 27 38 49 49 65 }[ 97 <76>]
( 76 ) { 13 27 38 49 49 65 }[ 97 (76)]
比较结束,将暂记最小元素与待排序序列第一个元素交换
( 76 ) { 13 27 38 49 49 65 }["97""76"]
( 76 ) { 13 27 38 49 49 65 }["76""97"]
更新待排序序列第一个元素为有序序列
( ) { 13 27 38 49 49 65 76 }[ 97 ]
8.第八趟排序(直接将最后一个待排序元素更新为有序序列)
( ) { 13 27 38 49 49 65 76 97 }
9.结果
{ 13 27 38 49 49 65 76 97 }
算法效率
无论情况好坏,比较次数KCN都固定为 n(n-1)/2 ≈ n²/2;
- 最好情况:待排序序列为顺序序列
- 移动次数RMN:0;
- 最坏情况:待排序序列为逆序序列
- 移动次数RMN:3(n-1);
所以时间复杂度为O(n²);
下面的代码是我按照自己的思路进行编写的,算法效率能达到上述的程度。
空间复杂度为O(1),交换时需要辅助空间。
算法特点
- 不稳定排序,因为交换元素导致的不稳定;
- 链式存储结构也适合;
- 移动次数较少。
算法代码
#include<iostream>
#include<ctime>
using namespace std;
void SelectSort(int* array, int n)
{
int recordMove = 0;
int recordCompare = 0;
for (int i = 1; i < n; i++)
{
//记录待排序序列暂记最小元素索引
//初始化为待排序序列中的第一个元素的索引
int minIndex = i;
//寻找暂记最小元素
for (int j = i + 1; j <= n; j++)
{
if (array[j] < array[minIndex]) {
minIndex = j;
}
recordCompare++;
}
//如果暂记最小元素不为待排序序列中的第一个元素
//即需要进行交换
if (minIndex != i)
{
int min = array[minIndex];
recordMove++;
array[minIndex] = array[i];
recordMove++;
array[i] = min;
recordMove++;
}
cout << "第" << i << "趟排序:" << endl;
for (int j = 1; j <= 16; j++)
{
if (j == 1) cout << " [ ";
if (j == i) cout << "< ";
cout << array[j] << " ";
if (j == i) cout << ">";
if (j == i) cout << " ] ";
}
cout << endl << endl;
}
cout << "比较次数:" << recordCompare << endl;
cout << "移动次数:" << recordMove << endl << endl;
}
int main()
{
//生成随机16个正整数
int positiveInteger[17];
time_t t;
srand((unsigned)time(&t));
cout << "生成16个2位正整数:" << endl;
for (int i = 1; i <= 16; i++)
{
positiveInteger[i] = (rand() % (100 - 10)) + 10;
cout << positiveInteger[i] << " ";
}
cout << endl << endl;
//选择排序
SelectSort(positiveInteger, 16);
cout << "排序后数组:" << endl;
for (int i = 1; i <= 16; i++)
{
cout << positiveInteger[i] << " ";
}
cout << endl;
system("pause");
return 0;
}
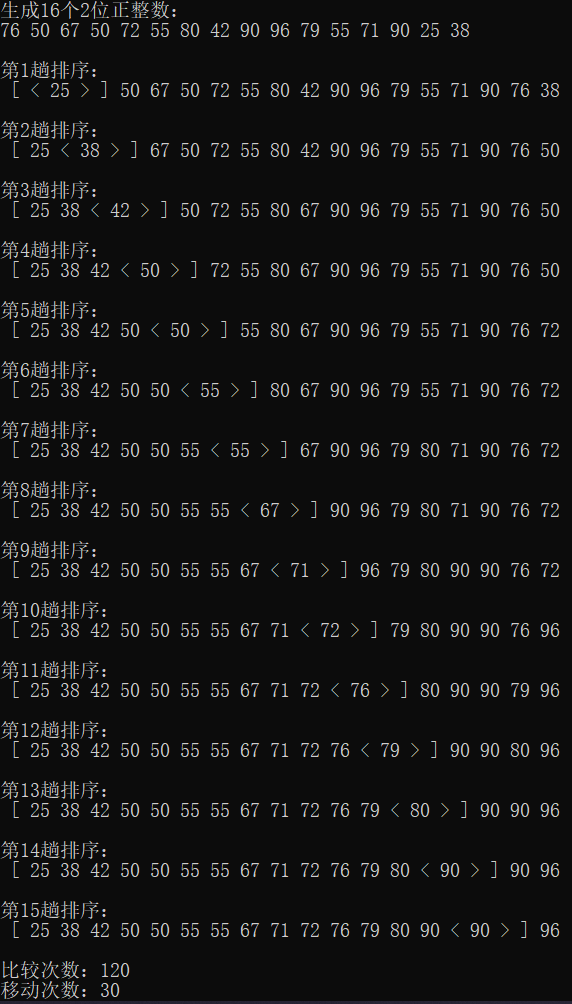
运行结果




 浙公网安备 33010602011771号
浙公网安备 33010602011771号