Kaggle竞赛——Titanic人员生还

1.引言    

提起泰坦尼克号，很多人会想到Jack和Rose的凄美爱情故事，当然还有这震惊的泰坦尼克号的沉没事件，我们很多人好奇一个人生还可能性，接下来慢慢着手分析。

2.背景

Kaggle是一个竞赛平台，集结了世界上很多的数据科学家以及相关的学者参与其中，通过Kaggle的知识竞赛平台，我们收集到泰坦尼克号乘员的相关信息。

 

其中有需求的技能，如二元分类，以及相关的编程语言Python或者R，当然也可以使用其他语言进行，我这里使用Python进行分析。

3.说明

 

在Data选项中我们会看到下面三个数据：

• train.csv，是数据集的训练数据，我们可以通过它进行训练模型。
• test.csv，是数据集的测试数据，用来测试我们的模型。
• gender_submission.csv，是一组假设仅所有女性都生存下来的测试结果。

4.初识数据

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.ensemble import RandomForestClassifier
import sklearn.preprocessing as preprocessing
from sklearn.model_selection import GridSearchCV, cross_val_score, StratifiedKFold, learning_curve

导入分析相关的所需要的库。

datas = pd.read_csv('train.csv')
datas.head()

通过pandas读取数据，以DataFrame的格式，我们可以看前5行的数据的样子：

通过这个表格，很容易知道这个数据有12列数据，表示出一个乘客有着12个特征数据，每一行代表一个客户：

• PassengerId   ->  乘客的ID
• Survived     ->  生存（0代表死亡，1代表生还）
• Pclass       ->  乘客等级（1、2、3等舱位）
• Name        ->  乘客姓名
• Sex         ->  乘客性别
• Age         ->  乘客年龄
• SibSp        ->  兄弟姐妹/配偶
• Parch        ->  父母/孩子
• Ticket       ->  船票
• Fare         ->  票价
• Cabin        ->  船舱
• Embarked      ->  登船的港口

了解了数据大概有什么属性后，再继续看看整体的数据，是否有缺失之类的情况。

datas.info()

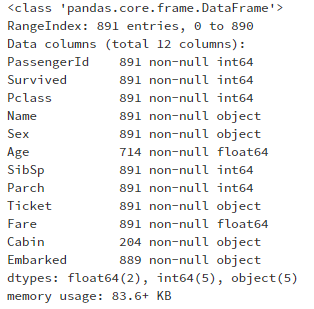
看到整体数据的情况，果然存在着缺失的情况，Embarked、Age少量缺失，Cabin严重缺失，Cabin严重缺失的情况我们可以直接删除，但是考虑该特征可能存在对结果有一定的重要性，先做保留处理。

再来看看描述统计的情况：

datas.describe()

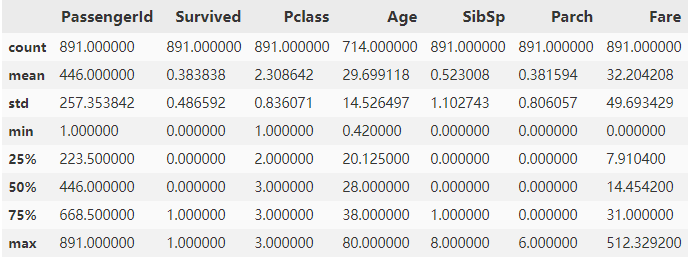
从这个统计中可以看出，只有38%的人员生还，3等舱的乘客很多，乘客的年龄在30岁左右，很少乘客和父母、孩子一起，512美元票价的乘客不到1%。

5.可视化

5.1 初步可视化

先来看看数据的大概的视图情况：

fig = plt.figure()

plt.subplot2grid((2,3),(0,0))
datas.Survived.value_counts().plot(kind='bar')
plt.title("获救情况 (1为获救)")
plt.ylabel("人数")

plt.subplot2grid((2,3),(0,1))
datas.Pclass.value_counts().plot(kind="bar")
plt.ylabel("人数")
plt.title("乘客等级分布")

plt.subplot2grid((2,3),(0,2))
plt.scatter(datas.Survived, datas.Age)
plt.ylabel("年龄")
plt.grid(b=True, which='major', axis='y')
plt.title("按年龄看获救分布 (1为获救)")

plt.subplot2grid((2, 3), (1, 0), colspan=2)
datas.Age[datas.Pclass == 1].plot(kind='kde')
datas.Age[datas.Pclass == 2].plot(kind='kde')
datas.Age[datas.Pclass == 3].plot(kind='kde')
plt.xlabel("年龄")
plt.ylabel("密度") 
plt.title("各等级的乘客年龄分布")
plt.legend(('头等舱', '二等舱', '三等舱'), loc='best')

plt.subplot2grid((2,3),(1,2))
datas.Embarked.value_counts().plot(kind='bar')
plt.title("各登船口岸上船人数")
plt.ylabel("人数")  
plt.show()

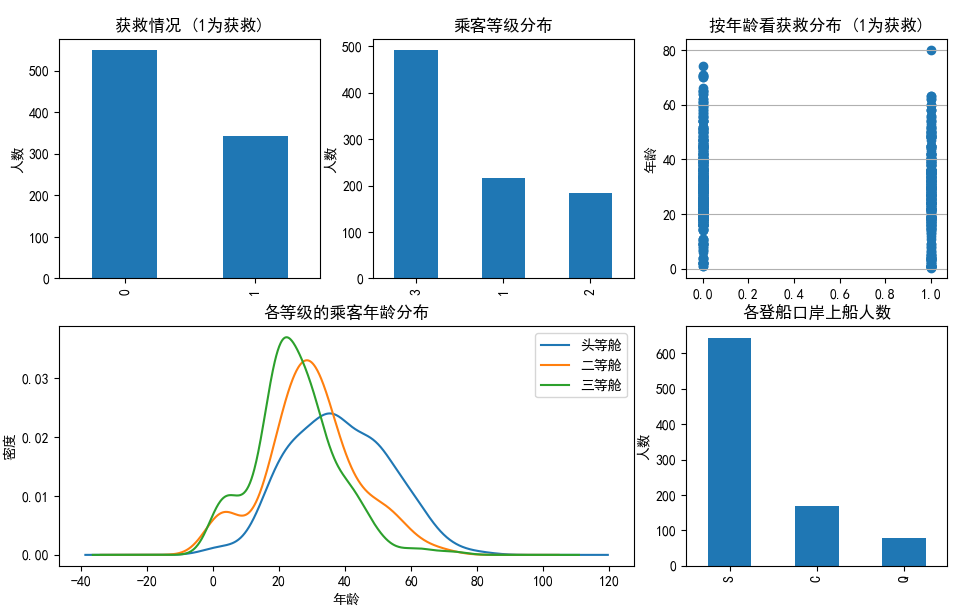
获救的人数只有300多人，3等舱的乘客有近500人，1等舱的乘客大部分年龄在40岁左右，2等舱的乘客年龄在30岁左右，3等舱在22岁左右，大部分是在S港口登录。

综合起来有了初步的认识：

不同等级的乘客，对生还的可能行有一定的影响。

年龄也对结果有一定的影响。

不同港口登录的乘客，存在很大的人数差，值得关注。

5.2 Pclass乘客等级

fig = plt.figure()

Survived_0 = datas.Pclass[datas.Survived == 0].value_counts()
Survived_1 = datas.Pclass[datas.Survived == 1].value_counts()
pclass = pd.DataFrame({'未获救': Survived_0, '获救': Survived_1})
pclass.plot(kind='bar', stacked=True)
plt.title('各等级乘客的获救情况')
plt.xlabel('乘客等级')
plt.ylabel('人数')
plt.show()

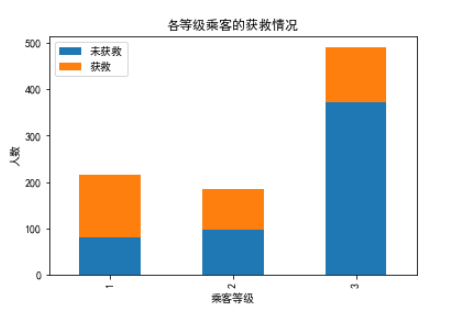
这个图更加证明了之前的猜想，高等级的舱位的乘客有着很大的生还可能性，尤其是1等舱的乘客，有半数多的乘客生还，相较于3等舱的乘客可怕的死亡率。

5.3 Sex性别

fig = plt.figure()

Survived_m = datas.Survived[datas.Sex == 'male'].value_counts()
Survived_f = datas.Survived[datas.Sex == 'female'].value_counts()
sex = pd.DataFrame({'男': Survived_m, '女': Survived_f})
sex.plot(kind='bar', stacked=True)
plt.title('性别特征的获救情况')
plt.xlabel('获救情况（1为获救）')
plt.ylabel('人数')
plt.show()

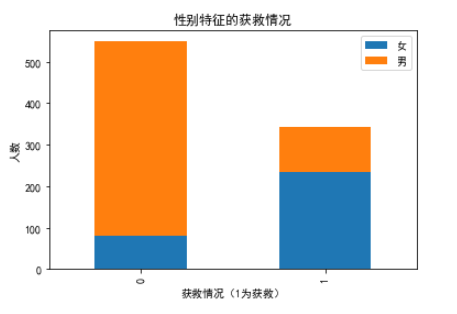
这个图很明显的表示了性别对结果有很强的影响，这说明生还中存在女士优先获救，大部分男性都死亡了。

5.4 Pclass和Sex

fig=plt.figure()
plt.title("根据舱等级和性别的获救情况")

ax1=fig.add_subplot(141)
datas.Survived[datas.Sex == 'female'][datas.Pclass != 3].value_counts().plot(kind='bar', label="女性高层舱", color='#FA2479')
ax1.set_xticklabels(["获救", "未获救"], rotation=0)
ax1.legend(["女性/高级舱"], loc='best')

ax2=fig.add_subplot(142, sharey=ax1)
datas.Survived[datas.Sex == 'female'][datas.Pclass == 3].value_counts().plot(kind='bar', label='女性底层舱', color='pink')
ax2.set_xticklabels(["未获救", "获救"], rotation=0)
plt.legend(["女性/低级舱"], loc='best')

ax3=fig.add_subplot(143, sharey=ax1)
datas.Survived[datas.Sex == 'male'][datas.Pclass != 3].value_counts().plot(kind='bar', label='男性高层舱',color='lightblue')
ax3.set_xticklabels(["未获救", "获救"], rotation=0)
plt.legend(["男性/高级舱"], loc='best')

ax4=fig.add_subplot(144, sharey=ax1)
datas.Survived[datas.Sex == 'male'][datas.Pclass == 3].value_counts().plot(kind='bar', label='男性底层舱', color='steelblue')
ax4.set_xticklabels(["未获救", "获救"], rotation=0)
plt.legend(["男性/低级舱"], loc='best')

plt.show()

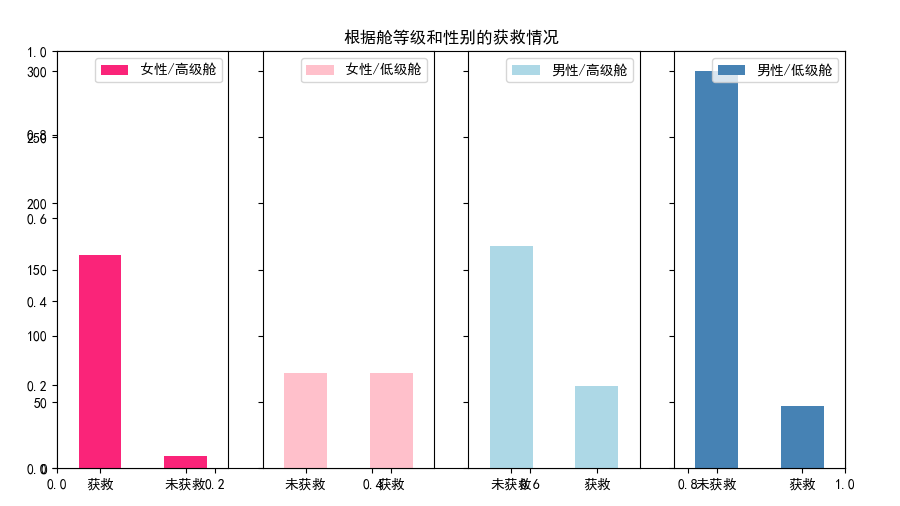
这个比较说明了性别特征对生还的可能性大于乘客等级，但是在男性中，等级有着强烈的优势。

5.5 Cabin船舱

fig = plt.figure()

Survived_cabin = datas.Survived[pd.notnull(datas.Cabin)].value_counts()
Survived_nocabin = datas.Survived[pd.isnull(datas.Cabin)].value_counts()
cabin = pd.DataFrame({'有船舱': Survived_cabin, '无船舱': Survived_nocabin})
cabin.plot(kind='bar', stacked=True)
plt.title('乘客有无船舱的情况')
plt.xlabel('生还情况(1为生还)')
plt.ylabel('人数')
plt.show()

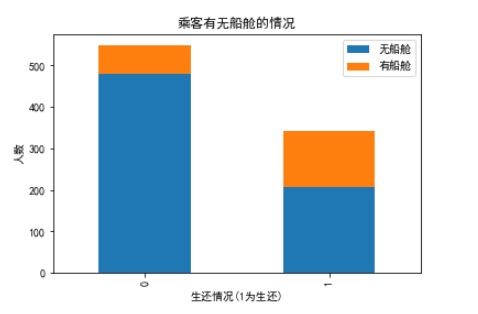
这说明有船舱的生还可能性大于没有船舱的可能性。

5.6 Embarked登录港口

fig = plt.figure()

Survived_0 = datas.Embarked[datas.Survived == 0].value_counts()
Survived_1 = datas.Embarked[datas.Survived == 1].value_counts()
embarked = pd.DataFrame({'未生还': Survived_0, '生还': Survived_1})
embarked.plot(kind='bar', stacked=True)
plt.title('不同登港口的生还情况')
plt.xlabel('登录港口')
plt.ylabel('人数')
plt.show()

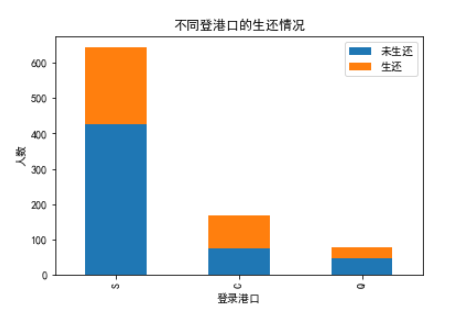
从图中看出，C港口登录的乘客有着高生还率，这说明登录港口有着一定的影响性。

5.7 SibSp和Parch

再来分析兄弟姐妹、配偶、父母孩子是否以这一定的影响性：

g = datas.groupby(['SibSp','Survived'])
df_sibsp = pd.DataFrame(g.count()['PassengerId'])
df_sibsp

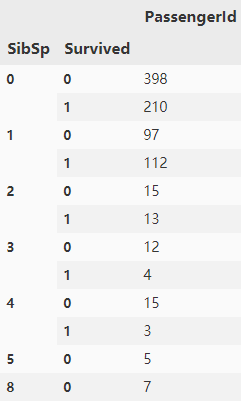
g = datas.groupby(['Parch','Survived'])
df_parch = pd.DataFrame(g.count()['PassengerId'])
df_parch

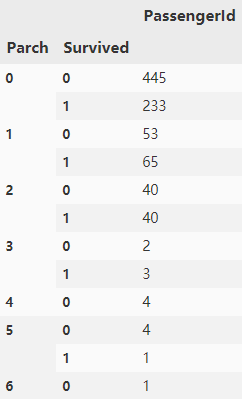
从这两个表格中，我们可以看出，其值在等于1的时候有着很高的生还率，那我们进行分析家庭成员是否有着一定影响：

datas["Fsize"] = datas["SibSp"] + datas["Parch"] + 1

g = sns.factorplot(x="Fsize",y="Survived",data = datas)
g = g.set_ylabels("生还的可能性")
g = g.set_xlabels('家庭成员')

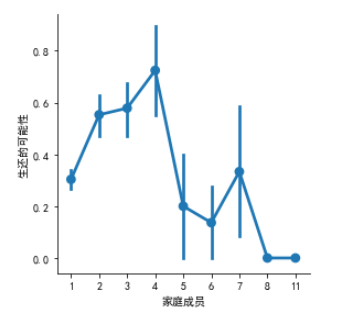
从图中可以明显的看出家庭成员有3-4个的时候，有着很高的生还率，我们保留家庭成员的特征。

5.8 Name 名字

datas['Name'].head()

分析Name属性的时候，发现每个人有不同的称呼，Mr、Mrs、Miss等等，我们来看看不同称呼是否有所影响：

data_title = [i.split(',')[1].split('.')[0].strip() for i in datas['Name']]
datas['Title'] = pd.Series(data_title)
g = sns.countplot(x='Title', data=datas)
g = plt.setp(g.get_xticklabels(), rotation=45)

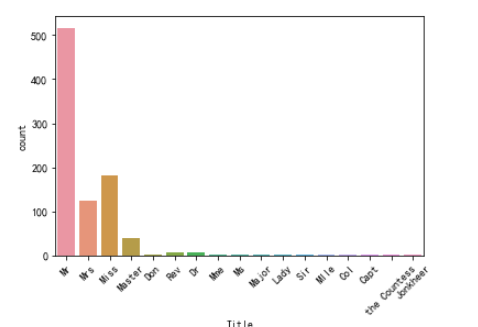
图中显示出了不同的称呼，我们来处理下不同的称呼：

datas['Title'] = datas['Title'].replace(['Lady', 'the Countess', 'Countess', 'Capt', 'Col', 'Don', 'Dr', 'Major', 'Rev', 'Sir', 'Jonkheer', 'Dona'], 'Rare')
datas['Title'] = datas['Title'].map({"Master": 0, 'Miss': 1, 'Ms': 1, 'Mme': 1, 'Mlle': 1, 'Mrs': 1, 'Mr': 2, 'Rare': 3})
datas['Title'] = datas['Title'].astype(int)

g = sns.countplot(datas["Title"])
g = g.set_xticklabels(["Master","Miss/Ms/Mme/Mlle/Mrs","Mr","Rare"])

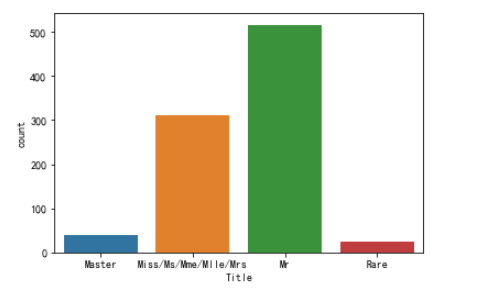
g = sns.factorplot(x="Title",y="Survived",data=datas,kind="bar")
g = g.set_xticklabels(["Master","Miss-Mrs","Mr","Rare"])
g = g.set_ylabels("生还的可能性")

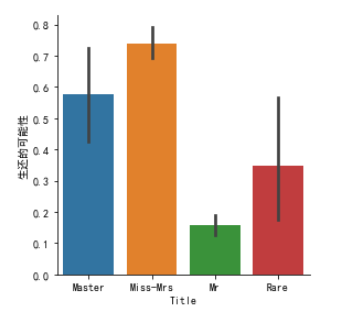
我们从图中发现，称呼对于生还性的影响还是很强烈，Miss-Mrs都达到了0.7以上，所以我们保留Name处理的Title属性。

我们已经可视化基本的特征属性，已经保留了两个新属性，以增强数据的准确性。

6. 特征工程

从之前的数据整体信息可以知道，数据集中存在不同type的数据，还有缺失的数据，我们就开始着手处理数据。

def set_missing_ages(df):
    '''
    这个函数是处理缺失的Age属性，利用随机森林的方法补充缺失的数据，以提高数据的准确性。
    '''
    age_df = df[['Age','Fare', 'Parch', 'SibSp', 'Pclass']]
    known_age = age_df[age_df.Age.notnull()].as_matrix()
    unknown_age = age_df[age_df.Age.isnull()].as_matrix()
    y = known_age[:, 0]
    X = known_age[:, 1:]
    rfr = RandomForestRegressor(random_state=0, n_estimators=2000, n_jobs=-1)
    rfr.fit(X, y)
    predictedAges = rfr.predict(unknown_age[:, 1::])
    df.loc[ (df.Age.isnull()), 'Age' ] = predictedAges 
    return df, rfr

def set_Cabin_type(df):
    '''
    处理缺失的Cabin属性，改变其为Yes和No
    '''
    df.loc[ (df.Cabin.notnull()), 'Cabin' ] = "Yes"
    df.loc[ (df.Cabin.isnull()), 'Cabin' ] = "No"
    return df

datas, rfr = set_missing_ages(datas)
datas = set_Cabin_type(datas)
datas.head()

通过函数的方法补全了缺失的Age、Cabin属性。

datas["Embarked"] = datas["Embarked"].fillna("S")

补全缺失的Embarked的值。

dummies_Cabin = pd.get_dummies(datas['Cabin'], prefix= 'Cabin')

dummies_Embarked = pd.get_dummies(datas['Embarked'], prefix= 'Embarked')

dummies_Sex = pd.get_dummies(datas['Sex'], prefix= 'Sex')

dummies_Pclass = pd.get_dummies(datas['Pclass'], prefix= 'Pclass')

df = pd.concat([datas, dummies_Cabin, dummies_Embarked, dummies_Sex, dummies_Pclass], axis=1)
df.drop(['PassengerId', 'Pclass', 'Sex', 'Ticket', 'Cabin', 'Embarked'], axis=1, inplace=True)
df.head()

处理了之前的数据集，将其转化成模型可识别的格式，并且删除了不可用的数据。

但是在仔细观察数据的时候发现，Age、Fare数值相对于其他数据过大，可能会对结果的准确性有所影响，于是我对数据的Age、Fare进行标准化处理：

scaler = preprocessing.StandardScaler()
age_scale_param = scaler.fit(df['Age'].values.reshape(-1, 1))
df['Age_scaled'] = scaler.fit_transform(df['Age'].values.reshape(-1, 1), age_scale_param)
fare_scale_param = scaler.fit(df['Fare'].values.reshape(-1, 1))
df['Fare_scaled'] = scaler.fit_transform(df['Fare'].values.reshape(-1, 1), fare_scale_param)

7. 随机森林建模

Y_train = df["Survived"]
X_train = df.drop(labels = ["Survived"],axis = 1)
kfold = StratifiedKFold(n_splits=10)
RFC = RandomForestClassifier()

rf_param_grid = {"max_depth": [None],
              "max_features": [1, 3, 10],
              "min_samples_split": [2, 3, 10],
              "min_samples_leaf": [1, 3, 10],
              "bootstrap": [False],
              "n_estimators" :[100,300],
              "criterion": ["gini"]}

gsRFC = GridSearchCV(RFC,param_grid = rf_param_grid, cv=kfold, scoring="accuracy", n_jobs= 4, verbose = 1)

gsRFC.fit(X_train,Y_train)

RFC_best = gsRFC.best_estimator_

gsRFC.best_score_

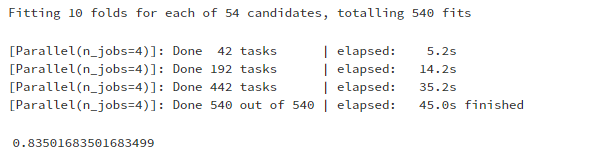
初始的简单优化模型，得出最好的低分结果为0.835 。