引言
大家好!今天我们将探讨一个经典的偏微分方程—拉普拉斯方程,并使用 Python 进行求解。拉普拉斯方程广泛应用于物理学中,尤其是在电磁学、流体力学和热传导等领域。通过这篇文章,你将了解什么是拉普拉斯方程,以及如何利用 Python 来数值求解它。
什么是拉普拉斯方程?
拉普拉斯方程是一种描述标量场(如电势、温度等)在静态情况下变化的偏微分方程。它的标准形式为:
其中:
- \(\nabla^2\) 是拉普拉斯算符,表示空间中二阶偏导数的和;
- \(\phi\) 是我们要解的标量场(如温度、电势等)。
拉普拉斯方程的物理意义是:在没有外部源项的情况下,标量场的变化是均匀的,场在空间中达到一个平衡状态。例如,在静电学中,拉普拉斯方程描述了没有电荷的区域中的电势分布;在热传导中,它描述了在稳态下温度的分布。
拉普拉斯方程的数值求解
拉普拉斯方程是一个二阶偏微分方程,解析解通常比较难以求得,因此我们常使用数值方法来求解。最常用的方法之一是有限差分法,它通过将连续的空间网格离散化为离散点来近似求解方程。
离散化拉普拉斯方程
对于二维的拉普拉斯方程,我们可以将空间网格离散化,将偏导数用差分来表示。假设我们在二维平面上,网格点的位置为 \((x_i, y_j)\),则拉普拉斯算符的离散化形式为:$$\frac{\phi_{i+1, j} - 2\phi_{i, j} + \phi_{i-1, j}}{(\Delta x)^2} + \frac{\phi_{i, j+1} - 2\phi_{i, j} + \phi_{i, j-1}}{(\Delta y)^2} = 0$$
其中,\(\phi_{i, j}\) 表示网格点 \((x_i, y_j)\) 处的场值,\(\Delta x\) 和 \(\Delta y\) 分别是 x 和 y 方向的网格步长。
通过这个差分公式,我们可以得到一个线性方程组,求解这个方程组即可得到整个网格的场值,从而得到标量场的分布。
如何用 Python 来求解?
下面,我们将通过一个简单的例子来展示如何使用 Python 求解拉普拉斯方程。我们将在一个二维区域内求解电势分布,假设电势在边界上已知,且区域内没有外部电荷。
安装必要的库
我们将使用 numpy 来进行数值计算,使用 matplotlib 来绘制结果。如果没有安装这些库,可以通过以下命令安装:
pip install numpy matplotlib
编写代码
# coding=utf-8
import matplotlib
matplotlib.use('Agg')
import numpy as np
import matplotlib.pyplot as plt
# 网格大小和步长
Lx, Ly = 10.0, 10.0 # x 和 y 方向上的大小
Nx, Ny = 50, 50 # x 和 y 方向上的网格点数
dx, dy = Lx / (Nx - 1), Ly / (Ny - 1) # 网格步长
# 创建网格
x = np.linspace(0, Lx, Nx)
y = np.linspace(0, Ly, Ny)
phi = np.zeros((Nx, Ny)) # 电势矩阵,初始值为0
# 设置边界条件:例如,左边界为电势为100,右边界为电势为0
phi[0, :] = 100 # 左边界
phi[-1, :] = 0 # 右边界
phi[:, 0] = 0 # 下边界
phi[:, -1] = 0 # 上边界
# 迭代求解拉普拉斯方程
tolerance = 1e-5 # 收敛误差
max_iter = 10000 # 最大迭代次数
for iteration in range(max_iter):
phi_new = phi.copy()
# 更新内部点的电势值
for i in range(1, Nx - 1):
for j in range(1, Ny - 1):
phi_new[i, j] = 0.25 * (phi[i + 1, j] + phi[i - 1, j] + phi[i, j + 1] + phi[i, j - 1])
# 检查收敛性
if np.max(np.abs(phi_new - phi)) < tolerance:
print(f"收敛于{iteration}次迭代")
break
phi = phi_new
# 绘制电势分布
plt.figure(figsize=(8, 6))
plt.contourf(x, y, phi.T, 50, cmap='jet')
plt.colorbar(label='Electric potential(V)')
plt.title("Numerical solution of Laplace's equation")
plt.xlabel('x')
plt.ylabel('y')
plt.savefig('Laplace.png')
代码解析
- 网格定义:我们首先定义了一个二维区域,其大小为 10x10,网格分辨率为 50x50。然后生成了 phi 矩阵,表示每个网格点上的电势值,初始值为 0。
- 边界条件:为模拟一个简单的情况,我们将左边界设置为 100V,右边界为 0V,上下边界设置为 0V。
- 迭代求解:我们使用有限差分法通过迭代的方式来求解内部点的电势。每次迭代,我们根据差分公式更新电势值,直到满足收敛条件为止。
- 结果可视化:最后,使用 matplotlib 绘制电势的等高线图,以直观显示解的分布。
运行结果
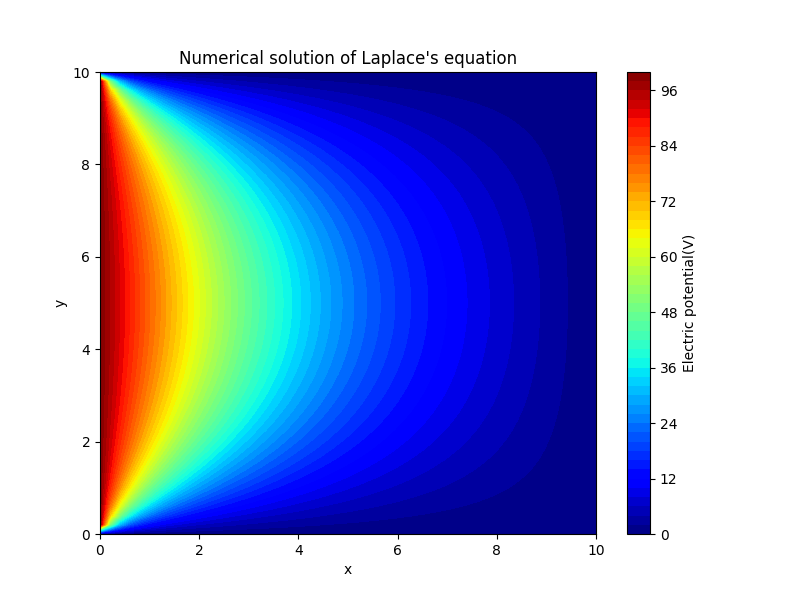
运行代码后,你将看到一个二维的电势分布图,显示了从左边界到右边界电势的变化。图中的颜色表示不同的电势值,左边界电势为 100V,右边界电势为 0V,整个区域的电势逐渐从左边界的 100V 降低到右边界的 0V。
总结
今天,我们使用 Python 和有限差分法求解了二维拉普拉斯方程,并通过数值方法得到了电势的分布。拉普拉斯方程在物理学中有着广泛的应用,理解并能够求解它,对于掌握电磁学、热力学等领域非常重要。
通过本文的示例,大家可以看到,拉普拉斯方程的求解并不复杂,只需要合理地离散化空间并迭代更新,便可以得到数值解。当然,这只是最基础的求解方法,随着问题的复杂性增加,还可以采用更高级的数值方法,如有限元法、谱方法等。
希望今天的内容对你有所帮助,欢迎在评论区提出问题和讨论!



