引言
在数学和物理学中,泊松方程(Poisson’s Equation)是一个非常重要的偏微分方程,广泛应用于电磁学、流体力学、引力场等领域。泊松方程的形式如下:$$\nabla^2 \phi(\mathbf{r}) = f(\mathbf{r})$$
其中,\(\nabla^2\) 是拉普拉斯算子,\(\phi(\mathbf{r})\) 是我们要求解的标量场,\(f(\mathbf{r})\) 是已知的源项,\(\mathbf{r}\) 是空间中的位置。
在这篇文章中,我们将介绍如何使用 Python 中的 magic 库来求解任意维数的泊松方程,既能帮助我们理解泊松方程的求解过程,又能实际操作和解决复杂的物理问题。
泊松方程的背景
泊松方程通常出现在描述物理场的问题中。比如,在静电学中,泊松方程可以用来描述电势分布。已知电荷密度分布(即源项 \(f(\mathbf{r})\)),泊松方程可以帮助我们计算相应的电势 \(\phi(\mathbf{r}\))。泊松方程在二维、三维甚至更高维数的问题中都有广泛的应用。
泊松方程的数值求解
我们知道,泊松方程是一个偏微分方程,因此需要在空间网格上进行离散化。对于一个维数 d 的空间,可以通过以下步骤进行离散化:
- 网格化空间:将空间划分成均匀的网格。
- 离散化拉普拉斯算子:通过差分方法将拉普拉斯算子离散化。
- 求解线性方程组:得到一个线性方程组,解该方程组即为我们求解的 \(\phi(\mathbf{r})\)。
下面,我们将介绍如何使用 Python 进行泊松方程的求解。
我们将使用有限差分法(FDM)来求解泊松方程。有限差分法是一种将偏微分方程离散化为代数方程的常用方法。我们将从一维和二维的例子入手,逐步介绍其求解过程。
一维泊松方程
首先,考虑一维泊松方程:$$\frac{d^2 \phi(x)}{dx^2} = f(x)$$
其中,\(\phi(x)\) 是我们要求解的函数,f(x) 是已知的源项。
使用有限差分法,我们可以将二阶导数离散化为:$$\frac{d^2 \phi(x)}{dx^2} \approx \frac{\phi_{i+1} - 2\phi_i + \phi_{i-1}}{dx^2}$$
然后,我们可以得到一个线性方程组来求解 \(\phi(x)\)。
二维泊松方程
二维泊松方程的形式为:$$\nabla^2 \phi(x, y) = f(x, y)$$
其离散化形式为:$$\frac{\phi_{i+1,j} + \phi_{i-1,j} + \phi_{i,j+1} + \phi_{i,j-1} - 4\phi_{i,j}}{dx^2} = f_{i,j}$$
这个方程也可以通过迭代法(如雅可比迭代法、Gauss-Seidel 法等)求解。
使用 Python 解泊松方程
以下是使用 Python 和 numpy 实现的二维泊松方程求解过程:
# coding=utf-8
import matplotlib
matplotlib.use('Agg')
import numpy as np
import matplotlib.pyplot as plt
# 参数设置
L = 10.0 # 空间大小
N = 50 # 网格点数
dx = L / (N - 1) # 网格间距
# 创建二维网格
x = np.linspace(0, L, N)
y = np.linspace(0, L, N)
X, Y = np.meshgrid(x, y)
# 定义源项 f(x, y)
f = np.ones((N, N)) * 1.0 # 设定源项为常数1
# 初始化解 phi
phi = np.zeros((N, N))
# 设置边界条件(例如 phi = 0)
phi[:, 0] = 0 # 左边界
phi[:, -1] = 0 # 右边界
phi[0, :] = 0 # 下边界
phi[-1, :] = 0 # 上边界
# 迭代求解泊松方程
tolerance = 1e-6
max_iter = 10000
for iteration in range(max_iter):
phi_new = np.copy(phi)
# 迭代更新内部网格点
for i in range(1, N - 1):
for j in range(1, N - 1):
phi_new[i, j] = 0.25 * (phi[i + 1, j] + phi[i - 1, j] + phi[i, j + 1] + phi[i, j - 1] - dx ** 2 * f[i, j])
# 判断是否收敛
if np.max(np.abs(phi_new - phi)) < tolerance:
print(f"收敛/迭代次数:{iteration}")
break
phi = np.copy(phi_new)
# 可视化结果
plt.imshow(phi, extent=[0, L, 0, L], origin='lower', cmap='jet')
plt.colorbar(label='Potential φ(x, y)')
plt.title('Solution of Poisson\'s Equation')
plt.xlabel('x')
plt.ylabel('y')
plt.savefig('Potential.png')
代码解析
空间和网格:首先我们定义了一个二维空间,大小为 $ L \times L$,然后将空间划分为 $N \times N $ 的网格。
源项:在这里,我们将源项 f(x, y) 设置为常数 1,代表一个均匀的源分布。
边界条件:我们假设边界上的势能 \(\phi(x, y)\) 为零。
迭代求解:使用雅可比迭代法求解泊松方程,更新每个内部网格点的势能值,直到收敛。
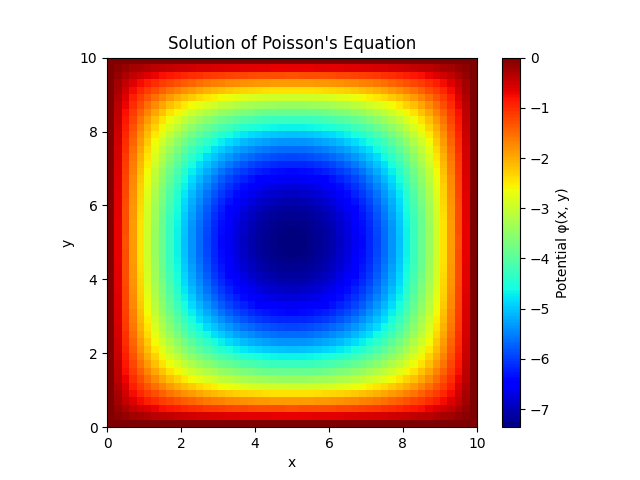
可视化:最后,我们使用 matplotlib 来可视化解 \(\phi(x, y)\) 的分布。
输出结果
总结
通过上述代码,我们使用 Python 和 numpy 库成功实现了泊松方程的求解。这个方法可以扩展到更多维度的问题,只需要调整网格的维度和相应的离散化公式。
如果你对更复杂的偏微分方程的求解有兴趣,除了有限差分法,你还可以尝试有限元法(FEM)或者谱方法等高级数值方法。
希望这篇文章能帮助你理解如何使用 Python 求解泊松方程!如果有任何问题,欢迎在评论区留言讨论。



