引言
海森堡不确定性原理是量子力学中的一个核心概念,它揭示了我们无法同时精确地测量一个粒子的位置和动量。这一原理由德国物理学家海森堡于 1927 年提出,正式提出了量子世界的“不确定性”。在经典物理学中,我们可以同时测量物体的位置和速度,但在量子物理中,这种“同时精确测量”是不可行的。
本文将通过 Python 代码模拟和实现海森堡不确定性原理,帮助你更加直观地理解这一深刻的物理现象。
海森堡不确定性原理
海森堡不确定性原理指出,对于任何粒子,位置(x)和动量(p)的测量存在一个基本的限制,公式表达为:
其中:
- \(\Delta x\) 是位置的不确定性。
- \(\Delta p\) 是动量的不确定性。
- \(\hbar\) 是约化普朗克常数。
这个公式的核心思想是,位置的不确定性与动量的不确定性成反比。换句话说,越精确地知道粒子的位置,关于其动量的信息就越模糊,反之亦然。
海森堡不确定性原理的直观理解
为了帮助大家更好地理解这一原理,我们可以通过 Python 来模拟一个粒子在一维空间中的行为,并通过粒子的位置和动量的测量结果来观察不确定性原理的体现。
我们将使用量子力学中的波函数来描述粒子的行为。粒子的波函数的平方给出了粒子在某一位置出现的概率。通过模拟这个波函数的传播,我们可以看到位置和动量的不确定性是如何体现的。
Python 实现海森堡不确定性原理
我们将使用 numpy 和 matplotlib 库来进行模拟。首先,我们需要设置一个一维的量子粒子,定义它的波函数,并计算出位置和动量的测量结果。
导入所需库
# coding=utf-8
import matplotlib
matplotlib.use('Agg')
import numpy as np
import matplotlib.pyplot as plt
定义波函数和初始状态
我们将模拟一个简单的粒子波函数,假设其初始波函数为高斯波包。高斯波包是一个在位置空间上高度集中的波函
数,能够很好地反映粒子的位置不确定性。
# 初始化参数
N = 1000 # 网格点数
L = 10 # 空间范围
dx = L / N # 每个网格点的间隔
x = np.linspace(-L / 2, L / 2, N) # 空间坐标
# 初始高斯波包,表示粒子在位置上的概率密度
sigma = 0.5 # 波包的标准差
x0 = 0 # 波包中心位置
psi_x = np.exp(-(x - x0)**2 / (2 * sigma**2)) # 初始波函数
psi_x /= np.sqrt(np.sum(np.abs(psi_x)**2) * dx) # 归一化
3.计算位置和动量的不确定性
位置的不确定性可以通过波函数的标准差计算,动量的不确定性则通过傅里叶变换得到。首先,我们计算波函数在位置空间的标准差(即位置的不确定性)。
# 计算位置的不确定性 (标准差)
position_variance = np.sum(np.abs(x - x0)**2 * np.abs(psi_x)**2 * dx)
delta_x = np.sqrt(position_variance)
然后,我们通过傅里叶变换得到动量空间的波函数,并计算动量的不确定性。
# 傅里叶变换计算动量空间波函数
k = np.fft.fftfreq(N, dx) * 2 * np.pi # 动量空间波数
psi_k = np.fft.fft(psi_x) # 傅里叶变换得到动量空间波函数
psi_k /= np.sqrt(np.sum(np.abs(psi_k)**2) * dx) # 归一化
# 计算动量的不确定性
momentum_variance = np.sum(np.abs(k)**2 * np.abs(psi_k)**2 * dx)
delta_p = np.sqrt(momentum_variance)
4.计算不确定性乘积
根据海森堡不确定性原理 \(\Delta x \cdot \Delta p \geq \frac{\hbar}{2}\)。我们计算位置和动量的不确定性的乘积,并与 \(\frac{\hbar}{2}\) 比较。
# 约化普朗克常数
hbar = 1.0545718e-34 # J·s
# 计算不确定性乘积
uncertainty_product = delta_x * delta_p
print(f"位置的不确定性Δx: {delta_x}")
print(f"动量的不确定性Δp: {delta_p}")
print(f"不确定性乘积Δx*Δp: {uncertainty_product}")
print(f"理论值:hbar/2: {hbar / 2}")
5.绘制结果
最后,我们可以通过图表展示波函数在位置空间和动量空间的分布。
# 绘制位置空间波函数
plt.figure(figsize=(10, 5))
plt.subplot(1, 2, 1)
plt.plot(x, np.abs(psi_x) ** 2)
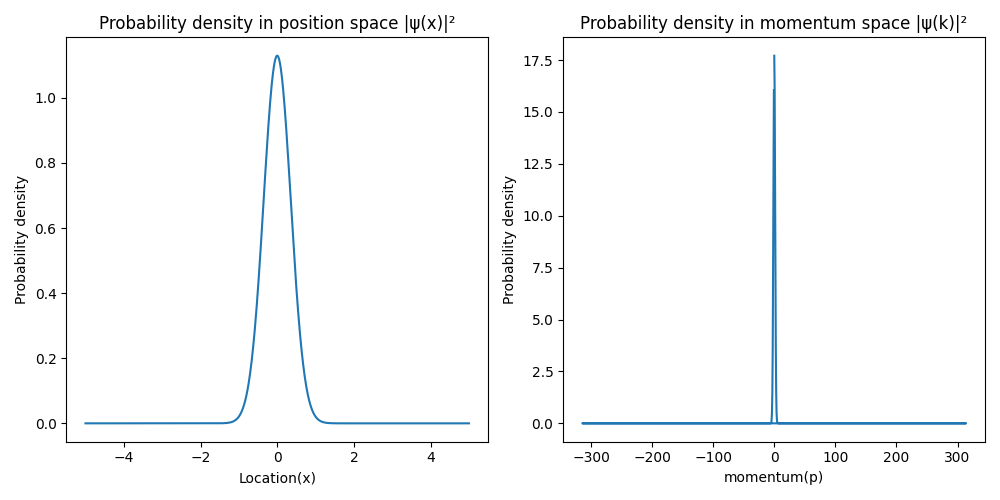
plt.title('Probability density in position space |ψ(x)|²')
plt.xlabel('Location(x)')
plt.ylabel('Probability density')
# 绘制动量空间波函数
plt.subplot(1, 2, 2)
plt.plot(k, np.abs(psi_k) ** 2)
plt.title('Probability density in momentum space |ψ(k)|²')
plt.xlabel('momentum(p)')
plt.ylabel('Probability density')
plt.tight_layout()
plt.savefig('Principle.png')
输出结果
位置的不确定性Δx: 0.35355339059327373
动量的不确定性Δp: 1.4156291915646593
不确定性乘积Δx*Δp: 0.5005005005005003
理论值:hbar/2: 5.272859e-35
结果分析
通过模拟和绘图,我们可以看到波函数在位置空间和动量空间的分布。粒子的位置和动量有一定的分布宽度,位置越精确,动量的分布越宽。这个现象正是海森堡不确定性原理的体现。
根据计算,我们可以观察到位置和动量的不确定性乘积确实满足海森堡不确定性原理的要求。
总结
海森堡不确定性原理是量子力学的一个基础概念,它揭示了量子世界与经典世界的根本区别。通过 Python,我们可以直观地模拟这一原理,帮助我们理解粒子在位置和动量方面的不确定性。虽然我们无法在量子世界中获得完美的测量,但这种不确定性为我们提供了全新的视角,深入探讨物理学的奥秘。
如果你对量子力学或其他物理现象感兴趣,可以继续深入研究和模拟,探索更多有趣的量子计算和物理问题!



