引言

在数学和拓扑学中，克莱因瓶(Klein bottle)是一个非常有趣且奇特的空间。它具有一种独特的性质—它是一个没有“边界”的二维流形，且具有非定向性。这个几何形状不像普通的立体形状那么直观，所以在可视化上可能会让人感到困惑。今天，我们将使用 Python 实现克莱因瓶的可视化，带你一探它的奇妙世界。

什么是克莱因瓶？

克莱因瓶是一个四维空间中的物体，但我们通常用三维空间来进行可视化。它可以通过在二维平面上进行特殊的拼接来构造，想象一下将一个矩形的两条相对边连接在一起，但是要小心地将一边翻转过来，这样就形成了一个没有“边界”的表面。

简单来说，克莱因瓶的特点是：

没有边界：不像环面(torus)那样有“洞”，克莱因瓶的表面是封闭的。

非定向性：如果你在克莱因瓶上画一个箭头并沿着表面移动，最终你会发现箭头会反向—这与我们在球面上移动的行为完全不同。

如何用 Python 实现克莱因瓶的可视化？

在 Python 中，我们可以借助 matplotlib 和 numpy 库来绘制克莱因瓶的三维图像。具体来说，我们将使用参数化方程来表示克莱因瓶，并通过三维图形进行绘制。

克莱因瓶可以通过如下的参数化方程来表示：

\[y(u, v) = \left( \sin(u) \left(1 + \sin(v)\right) \right) z(u, v) = \left( \cos(v) \right)\]

其中，u 和 v 是参数，分别在区间 [0, 2π] 和 [0, π] 上变化。通过这种方式，我们可以在三维空间中生成克莱因瓶的几何图形。

Python代码实现

让我们通过Python代码实现克莱因瓶的可视化。

安装依赖库

首先，需要安装matplotlib和numpy，可以通过以下命令安装：

pip install matplotlib numpy

编写代码实现克莱因瓶的可视化

# coding=utf-8
import matplotlib

matplotlib.use('Agg')
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D


# 克莱因瓶的参数化方程
def klein_bottle(u, v):
    # 这里我们增加自交的效果，形成一个近似克莱因瓶的形态
    x = (np.cos(u) * (1 + np.sin(v)))  # 控制水平的X轴坐标
    y = np.sin(u) * (1 + np.sin(v))  # 控制水平的Y轴坐标
    z = np.cos(v)  # 控制垂直的Z轴坐标
    return x, y, z


# 设置参数u和v的范围
u = np.linspace(0, 2 * np.pi, 100)  # u方向的参数，从0到2pi
v = np.linspace(0, np.pi, 50)  # v方向的参数，从0到pi
u, v = np.meshgrid(u, v)

# 计算克莱因瓶的坐标
x, y, z = klein_bottle(u, v)

# 绘制克莱因瓶的三维图形
fig = plt.figure(figsize=(10, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制表面
ax.plot_surface(x, y, z, rstride=1, cstride=1, color='b', edgecolor='none')

# 设置图形标题和标签
ax.set_title("Klein Bottle Visualization")
ax.set_xlabel("X")
ax.set_ylabel("Y")
ax.set_zlabel("Z")

# 调整图形的视角，使其更易观察
ax.view_init(elev=30, azim=30)

# 保存图形
plt.savefig('Klein.png')

代码解析

  1. 定义克莱因瓶的参数化方程：klein_bottle(u, v)函数根据上面的参数化方程计算每个点的坐标。
  2. 设置参数的范围：我们使用np.linspace设置参数u和v的范围，其中u从0到 \(2\pi\)，而v从0到 \(\pi\)。
  3. 计算克莱因瓶的坐标：通过np.meshgrid生成u和v的网格，然后使用这些值计算出克莱因瓶的三维坐标。
  4. 绘制三维图形：使用matplotlib中的plot_surface方法绘制表面，并设置图形标题和轴标签。

运行结果

运行上述代码后，你将看到一个3D图形，展示了克莱因瓶的可视化。它将以蓝色填充，边缘没有明显的界限，这正是克莱因瓶的特点。你可以通过旋转图形来观察克莱因瓶的不同角度，感受其独特的几何结构。

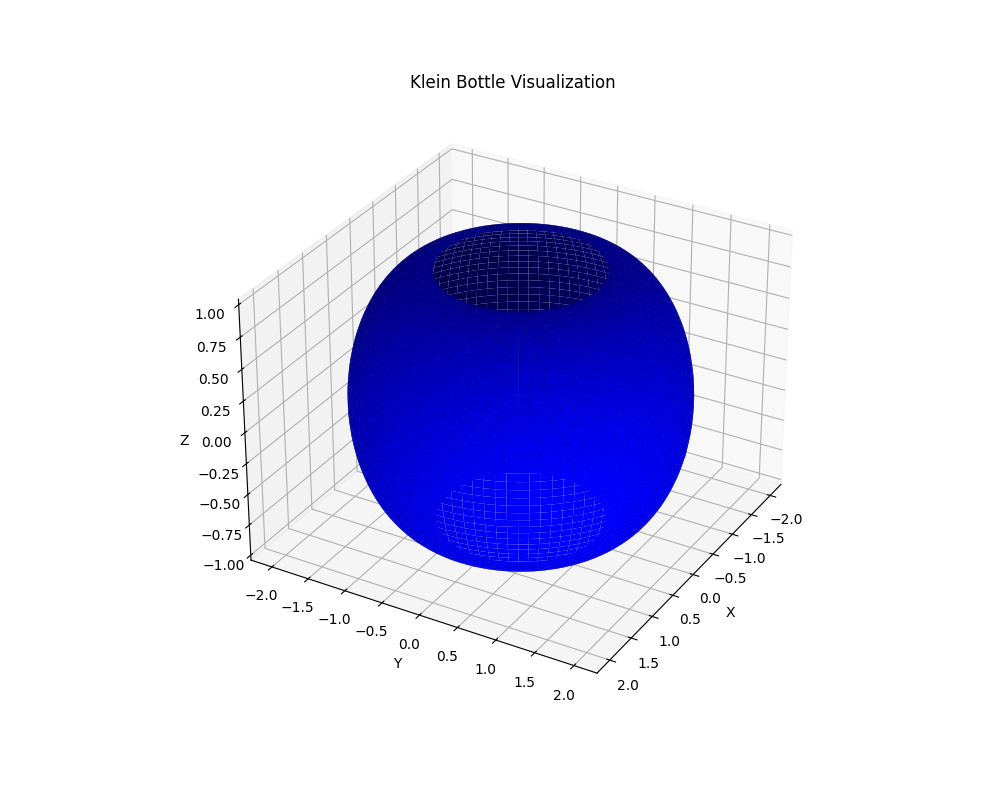
总结

克莱因瓶是一个非常有趣的数学概念，通过Python的强大绘图库，我们可以轻松地将这一抽象的几何形状可视化出来。使用matplotlib和numpy，我们能够通过参数化方程精确地绘制出克莱因瓶，并帮助我们更好地理解它的结构和性质。

希望通过这篇文章，你能够对克莱因瓶有更深入的了解，并掌握如何使用Python进行数学模型的可视化。数学和编程的结合不仅能够帮助我们更好地理解复杂的概念，还能让我们对这些概念产生更多的兴趣与探索。