快速幂

快速幂

ll qpow(ll x, ll y, ll mod){
	ll ret = 1;
	while(y){
		if(y & 1)	ret = (ret % mod * x % mod) % mod;
		x = (x % mod * x % mod);
		y >>= 1;
	}
	return ret;
}

例题
cf 1362E

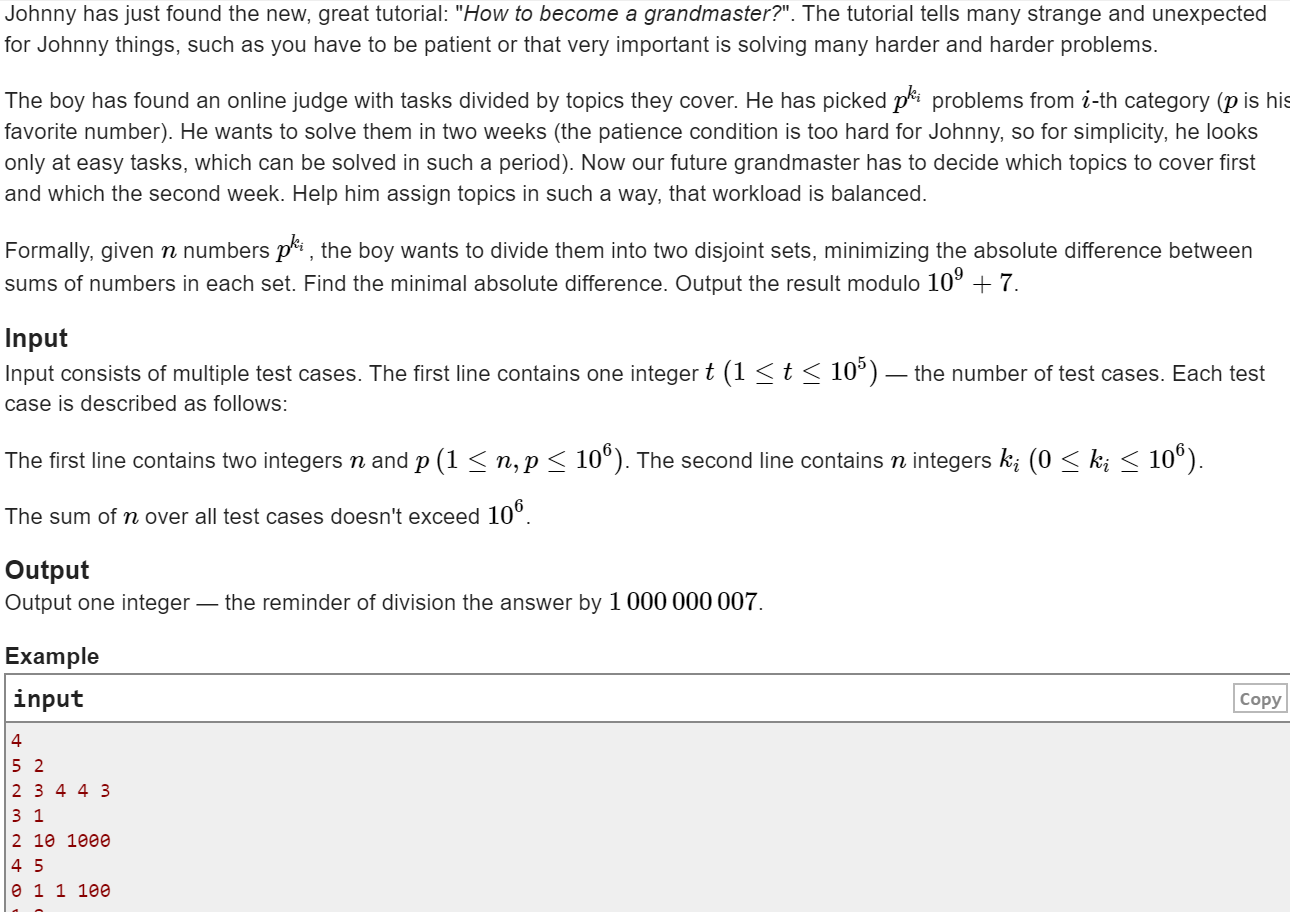
题目大概的意思就是
给你一个p是底数
n个数是 p 的指数
将这些 p的幂乘 分为两组
使两组数的和 差值最小
所以就从大到小一个一个给 可以发现当你将一个大数给了一组以后，接下来的数一定是 要么将这个大数抵消，要么不够
因为 可以将这些数看作 p进制 的 10000 这样的 1 后面 n 个0 ；那么对于一个大的数 不存在小于等于的数 相加不经过它，直接跳过它
那么只需要 在将一个大数给了一组后 持续的减去后面的数， 一直到零，继续将 当前的大数给 一组
重点 快速幂函数

题目中可能存在 差值 为 mod 的情况
所以判断ans = 0 不能通过单一 的 mod
可以在选择一个 mod 这样双 mod 都为 0 的情况 就是 真的为 0 了

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std;
typedef long long ll;
const int maxn = 1e6 + 10;
ll t, n, p;
ll mod1 = 1e9 + 7;
ll mod2 = 1e9 + 3;
ll qpow(ll x, ll y, ll mod){
	ll ret = 1;
	while(y){
		if(y & 1)	ret = (ret % mod * x % mod) % mod;
		x = (x % mod * x % mod);
		y >>= 1;
	}
	return ret;
}
ll a[maxn];
int main(){
	scanf("%lld", &t);
	while(t--){
		scanf("%lld %lld", &n, &p);
		for(int i = 0; i < n; ++ i)
			scanf("%lld", &a[i]);
		sort(a, a+n);
		ll ans1 = 0, ans2 = 0;
		for(int i = n-1; i >= 0; -- i){
			ll temp1 = qpow(p, a[i] , mod1), temp2 = qpow(p, a[i], mod2);
			if(ans1 == 0 && ans2 == 0)	ans1 = temp1, ans2 = temp2;
			else	ans1 = (ans1 - temp1 + mod1) % mod1, ans2 = (ans2 - temp2 + mod2) % mod2;
                        //可能temp1 > ans1 在这种情况下 ans1 是 ans1 + k * mod1（ k >=  1)一定是大于 temp1  所以从 k 中拿一个 mod 就行了 
		}
		printf("%lld\n", ans1);
	}
}