算法第五章作业报告

 

7-2 最小重量机器设计问题 (25 分)

设某一机器由n个部件组成，每一种部件都可以从m个不同的供应商处购得。设wij​是从供应商j 处购得的部件i的重量，cij​是相应的价格。 试设计一个算法，给出总价格不超过d的最小重量机器设计。

输入格式:

第一行有3 个正整数n ，m和d， 0<n<30, 0<m<30, 接下来的2n 行，每行m个数。前n行是c，后n行是w。

输出格式:

输出计算出的最小重量，以及每个部件的供应商

输入样例:

3 3 4

1 2 3

3 2 1

2 2 2

1 2 3

3 2 1

2 2 2

结尾无空行

输出样例:

在这里给出相应的输出。例如：

4

1 3 1

1.1 说明“最小重量机器设计问题"的解空间

解空间为每个部件选择的供应商，解空间的长度为n的1-3向量组成，即每个部件都可从m个供应商中选。

1.2 说明 “最小重量机器设计问题"的解空间树

 

 

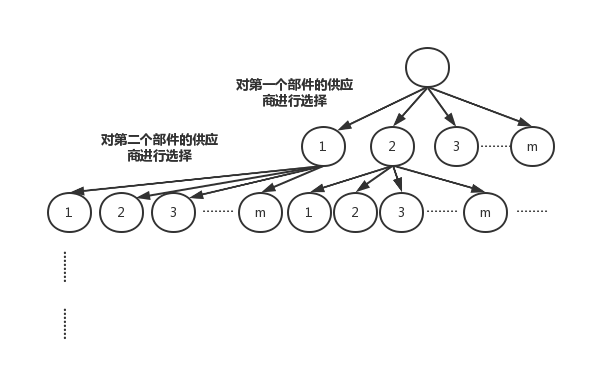
1.3 在遍历解空间树的过程中，每个结点的状态值是什么

noww 当前总重量

nowc 当前总价格

x[] 数组存放 当前对应每个部件的供应商

ans 满足条件的最小重量

res[] 数组存放 最终重量为ans对应每个部件的供应商

代码

#include <bits/stdc++.h>　　
#define INF 0x3f3f3f3f　　
using namespace std;
const int N = 35;
int n, m, d;
int ans, noww, nowc;
int x[N];
int res[N];
int c[N][N], w[N][N];
void dfs(int u) 
{
    if(u > n) {
        if(noww < ans) {
            ans=noww;
            for (int i=1; i<=n; i++) {
                res[i]=x[i];
            }
        }
    }
    else {
        for (int i=1; i<=m; i++) {
            if(nowc+c[u][i]<=d&&noww+w[u][i]<ans) {
                nowc+=c[u][i];noww+=w[u][i];
                x[u]=i;
                dfs(u+1);
                nowc-=c[u][i];noww-=w[u][i];
            }
        }
    }
}
int main() {
    ans=INF;
    scanf("%d%d%d", &n, &m, &d);
    for (int i=1; i<=n; i++) {
        for (int j=1; j<=m; j++) {
            scanf("%d", &c[i][j]);
        }
    }
    for (int i=1; i<=n; i++) {
        for (int j=1; j<=m; j++) {
            scanf("%d", &w[i][j]);
        }
    }
    dfs(1);
    
    
    printf("%d\n", ans);
    for (int i=1; i<=n; i++) {
        printf("%d ", res[i]);
    }
    printf("\n");
    
    return 0;
}

 

2. 你对回溯算法的理解

回溯算法之精髓在于回溯，即退回原状态。

回溯算法之精炼在于剪枝，即剪除不满足约束条件的路径或剪去得不到问题的解或最优解的路径。