三、栈和队列（栈、队列）

一、栈

后进先出（Last In First Out，LIFO）的线性序列被称为“栈”。栈也是一种线性表，只不过是操作受限的线性表，只能在一端进行进出操作。进出的一端被称为栈顶，另一端被称为栈底。栈可以采用顺序存储，也可以采用链式存储，分别被称为顺序栈和链栈。

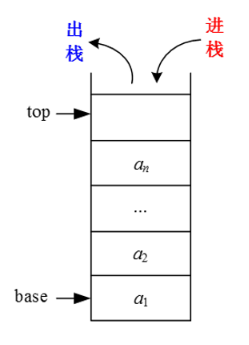
1.1 顺序栈

1.1.1 顺序栈的定义

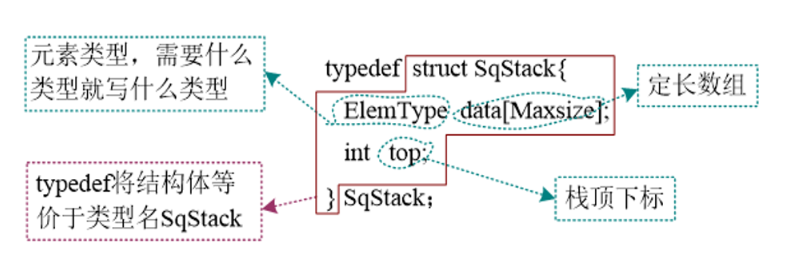
1.1.1.1 顺序栈的静态定义

/*
    1. 定长数组
    2. 栈顶下标  top指向的永远是一个空的空间
*/
#define MaxSize 100
typedef struct SqStack
{
    ElemType data[MaxSize];  // 定长数组
    int top;                 // 栈顶下标, 指向的永远是一个空的空间
}SqStack;

 

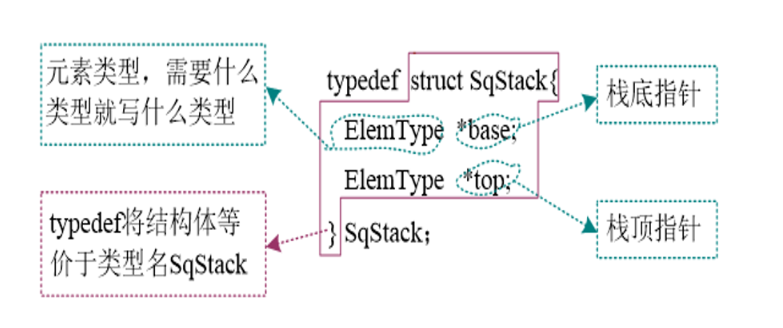
1.1.1.2 顺序栈的动态定义

// 初始的时候，top 与 base 指向同一个空间，然后 top++， base不变
typedef struct SqStack
{
    ElemType *base; // 栈底指针
    ElemType *top;  // 栈顶指针
}SqStack;

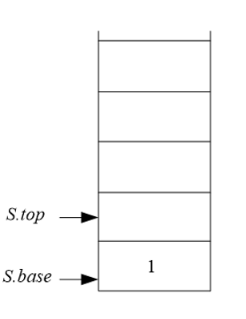
1.1.2 顺序栈的初始化

/*
    初始化一个空栈，动态分配Maxsize大小的空间，用S.top和S.base指向该空间的基地址。
*/
bool InitStack(SqStack &S)
{
    S.base = new int[MaxSize];
    if(S.base == NULL)
    {
        return false;
    }
    S.top = S.base;
    return true;
}

1.1.3 顺序表的入栈

/*
    入栈前要判断是否栈满，如果栈已满，则入栈失败；否则将元素放入栈顶，栈顶指针向上移动一个位置（top++）。
*/
bool Push(SqStack &S, int value)
{
    if(S.top - S.base == MaxSize)
    {
        return false;  // 栈满了
    }
    // *(S.top++) = value;
    *(S.top) = value;
    S.top++;
    return true;
}

1.1.4 顺序栈的出栈

/*
    出栈前要判断是否栈空，如果栈是空的，则出栈失败；否则将栈顶元素暂存给一个变量，栈顶指针向下移动一个空间（top--）。
*/
bool Pop(SqStack &S, int &value)
{
    if(S.base == S.top)
    {
        return false;
    }
    // value = *(--S.top)
    S.top = S.top-1;
    value = *(S.top);
    return true;
}

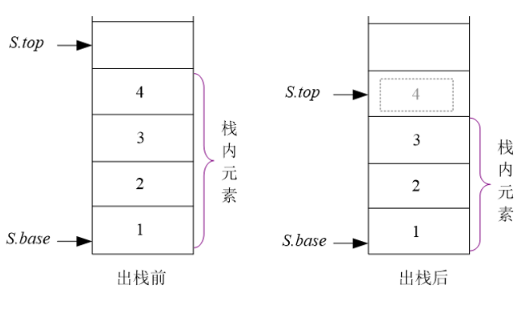
1.1.5 顺序栈的取栈顶元素

/*
    取栈顶元素和出栈不同，栈顶指针未移动，栈内元素个数未变。而出栈是指栈顶指针向下移动一个位置，栈内不再包含这个元素。
*/
int GetTop(SqStack &S)
{
    if(S.top != S.base)
    {
        return *(S.top-1);
    }
    else 
    {
        return -1;
    }
}

1.1.6 顺序栈的算法时间复杂度

1.1.7 顺序栈的代码整合

 

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<string>
using namespace std;
#define Maxsize 100

typedef struct
{
    int *base; // 栈底指针
    int *top;  // 栈顶指针
}SqStack;

// 栈初始化
bool InitSqStack(SqStack &S)
{
    S.base = new int[Maxsize];
    if (S.base == NULL)
    {
        return false;
    }
    S.top = S.base;
    return true;
}

// 入栈操作
bool PushStack(SqStack &S, int value)
{
    if (S.top - S.base == Maxsize) // 栈满
    {
        return false;
    }
    *(S.top) = value;
    S.top++; // 元素 value e压入栈顶，然后栈顶指针加1，等价于*S.top = value; S.top++;
    return true;
}

// 获取栈顶元素
int GetTop(SqStack &S)
{
    if (S.top == S.base)
    {
        return -1;
    }
    return *(S.top - 1);
}

// 出栈操作
bool PopStack(SqStack &S, int &ret)
{
    if (S.base == S.top)
    {
        return false;
    }
    ret = *(--S.top);
    return true;
}
int main()
{
    int count, value, ret;
    SqStack S;
    // 初始化栈
    if (InitSqStack(S))
    {
        cout << "栈初始化成功！" << endl;
    }
    else
    {
        cout << "栈初始化失败！" << endl;
        return -1;
    }
    cout << "请输入栈的元素个数: ";
    cin >> count;
    for (int i = 1; i <= count; i++)
    {
        cout << "请输入入栈的第 "<< i << " 元素: ";
        cin >> value;
        if (PushStack(S, value))
        {
            cout << "第 " << i << " 个元素: " << value << " 入栈成功！" << endl;
        }
        else
        {
            cout << "栈满了，入栈失败" << endl;
        }
    }
    cout << "元素依次出栈: " << endl;
    while (S.top != S.base)
    {
        cout << "栈顶元素是: " << GetTop(S);
        PopStack(S, ret);
        cout << "  元素: " << ret << "出栈成功" << endl;
    }
    return EXIT_SUCCESS;
}

1.2 链栈

栈可以用顺序存储，也可以用链式存储。

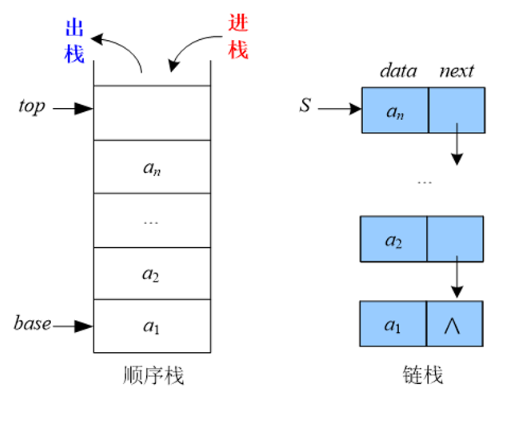
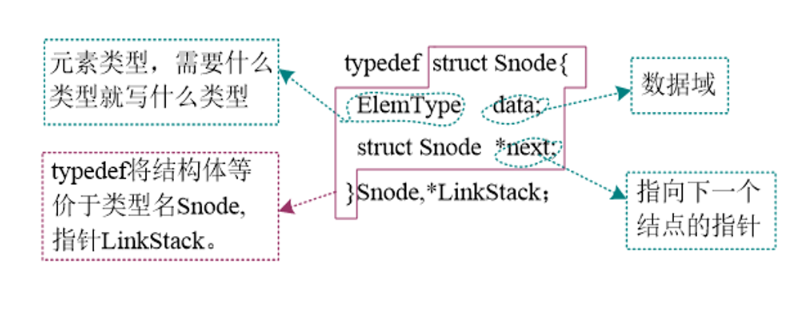
1.2.1 链栈的定义

/*
    链栈本质上就是一个单链表
*/
typedef struct Snode
{
    ElemType data;
    struct Snode *next;
}Snode, *LinkStack;

1.2.2 链栈的初始化

/*
    初始化一个空栈，链栈是不需要头结点的，因此只需要让栈顶指针为空即可。
*/
bool InitStack(LinkStack &S)
{
    S = NULL;
    return true;
}

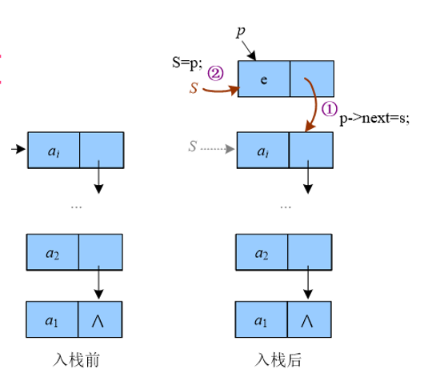
1.2.3 链栈的入栈

/*
    入栈是将新元素结点压入栈顶，将新元素结点插入到第一个结点的前面，然后修改栈顶指针。
*/
bool Push(LinkStack &s, int vale)
{
    LinkStack p;
    p = new Snode;
    p->data = value;
    p->next = S;
    S = p;
    return true;
}

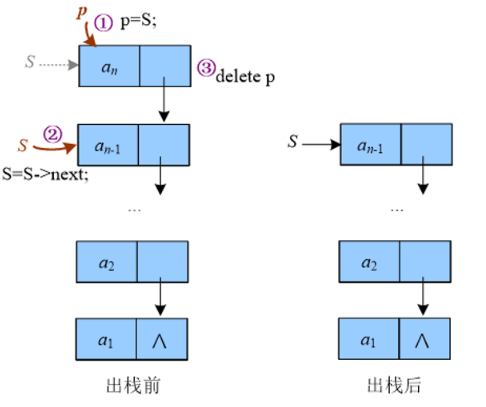
1.2.4 链栈的出栈

/*
    出栈是把栈顶元素删除，栈顶指针指向下一个结点，然后释放空间。
*/
bool Pop(LinkStack &S, int &ret)
{
    LinkStack p;
    if(S == NULL)
    {
        return false;
    }
    ret = S->data;
    p = S;
    S = S->next;
    delete p;
    return true;
}

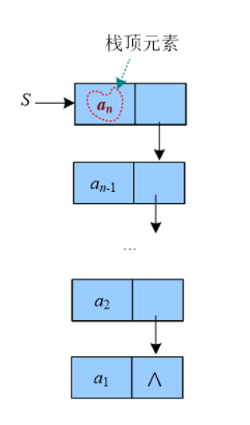
1.2.5 链栈的取栈顶元素

/*
    取栈顶元素和出栈不同，取栈顶元素只是把栈顶元素复制一份，栈顶指针没变。
*/
int GetTop(LinkStack &S)
{
    if(S != NULL)
    {
        return S->data;
    }
    return -1;
}

2.2.6 链栈的算法时间复杂度

2.2.7 链栈的代码整合

 

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<string>
using namespace std;

typedef struct Snode
{
    int data;            // 数据域
    struct Snode *next;  // 指针域
}Snode, *LinkStack;

// 链栈初始化
bool InitStack(LinkStack &S)
{
    S = NULL;    // 链栈不需要头结点，所以直接为NULL
    return true;
}

// 链栈入栈
bool PushStack(LinkStack &S, int value)
{
    LinkStack p;
    p = new Snode;
    p->data = value;
    p->next = S;
    S = p;
    return true;
}

// 链栈出栈
bool PopStack(LinkStack &S, int &ret)
{
    if (S == NULL)
    {
        return false;
    }
    LinkStack p;
    ret = S->data;
    p = S;
    S = S->next;
    delete p;
    return true;
}

// 获取链栈的栈顶元素
int GetTop(LinkStack &S)
{
    if (S == NULL)
    {
        return - 1;
    }
    return S->data;
}
int main()
{
    int count, value, ret;
    LinkStack S;
    cout << "链栈初始化" << endl;
    if (InitStack(S))
    {
        cout << "链栈初始化成功！" << endl;
    }
    else
    {
        cout << "链栈初始化失败" << endl;
        return -1;
    }
    cout << "请输入链栈的元素个数: ";
    cin >> count;
    for (int i = 1; i <= count; i++)
    {
        cout << "请输入第 " << i << " 个元素的值: ";
        cin >> value;
        if (PushStack(S, value))
        {
            cout << "元素 " << value << " 入栈成功！" << endl;
        }
        else
        {
            cout << "栈满了， 元素入栈失败" << endl;
        }
    }
    cout << "链栈依次出栈" << endl;
    while (S != NULL)
    {
        cout << "栈顶元素是: " << GetTop(S);
        PopStack(S, ret);
        cout << "  元素: " << ret << "出栈成功" << endl;
    }
    return EXIT_SUCCESS;
}

二、队列

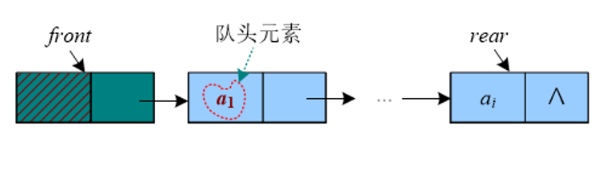
　　先进先出（First In First Out，FIFO）的线性序列，被称为“队列”。队列也是一种线性表，只不过它是操作受限的线性表，只能在两端操作：从一端进，从另一端出。进的一端被称为队尾（rear），出的一端被称为队头（front）。队列可以采用顺序存储，也可以采用链式存储。

 

 

 

2.1 顺序队列

2.1.1 顺序队列的定义

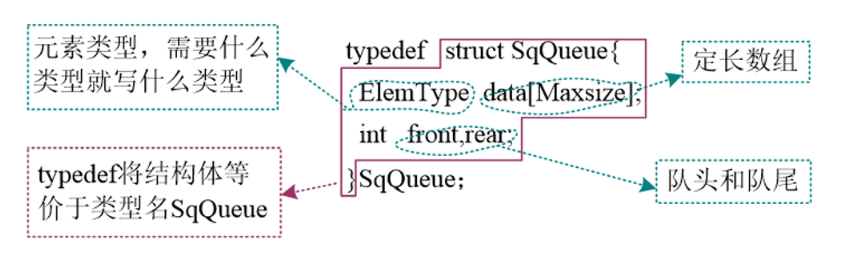
2.1.1.1 顺序队列的静态定义

typedef struct SqQueue
{
    ElemType data[MaxSize];
    int front, rear;
}SqQueue;

 

 

2.1.1.2 顺序队列的动态定义

typedef struct SqQueue
{
    ElemType *base;
    int front, rear;
}SqQueue;

 

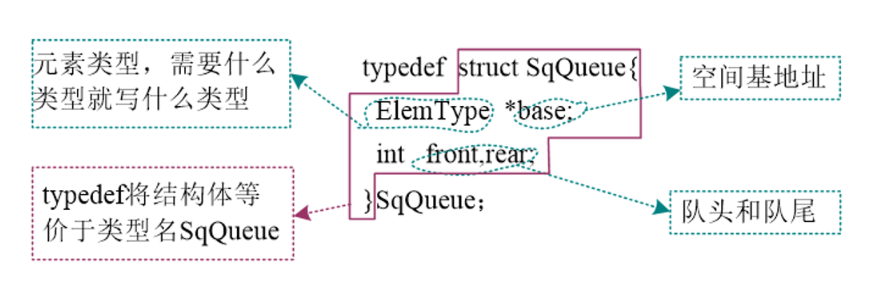
2.1.2 顺序队列的假溢出

明明有空间，却出现了队满的情况，这种情况称为“假溢出”。

 

2.1.3 循环队列

2.1.3.1 循环队列的队空

// 循环队列队空的判定条件：Q.front==Q.rear。

// 初始化
bool InitQueue(SqQueue &Q)
{
    Q.base = new int[MaxSize];
    if(Q.base == NULL)
    {
        return false;
    }
    Q.front = Q.rear = 0;
    return true;
}

// 循环队列的队头
int GetHead(SqQueue &e)
{
    if(Q.front == Q.rear)
    {
        return -1;
    }
    return Q.base[Q.front]
}

 

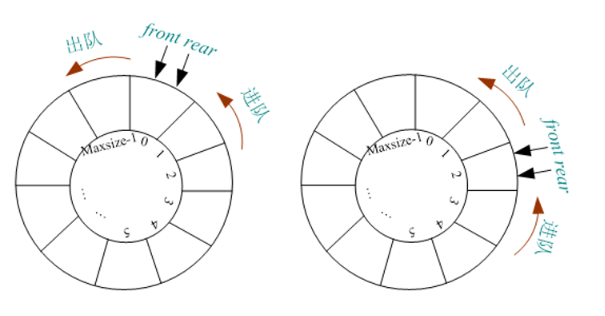
2.1.3.2 循环队列的队满

循环队列队满的判定条件：(Q.rear+1)%Maxsize==Q.front。

 

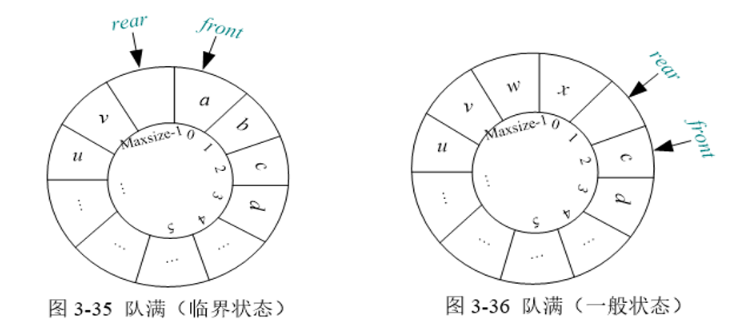
2.1.3.3 循环队列的入队

/*
    入队时，首先将元素x放入Q.rear所指空间，然后Q.rear后移一位。
    Q.base[Q.rear]=x;                       //将元素x放入Q.rear所指空间
    Q.rear=(Q.rear+1) %Maxsize;    //Q.rear后移一位
*/
bool EnQueue(SqQueue &Q, int value)
{
    if((Q.rear + 1) % MaxSize == Q.front)
    {
        return false;
    }
    Q.base[Q.rear] = value;
    Q.rear = (Q.rear + 1) % MaxSize;
    return true;
}

 

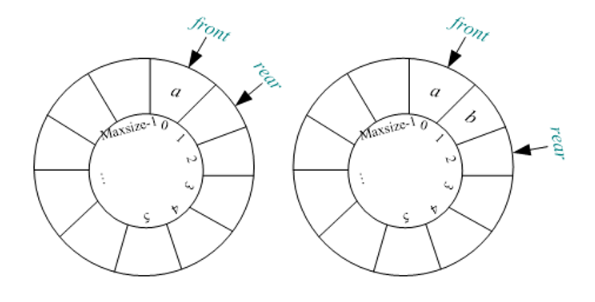
2.1.3.4 循环队列的出队

/*
    先用变量保存队头元素，然后队头Q.front后移一位。
    e=Q.base[Q.front];                       //用变量记录Q.front所指元素，
    Q.front=(Q.front+1) %Maxsize;   // Q. front向后移一位
*/
bool DeQueue(SqQueue &Q, int &ret)
{
    if(Q.front == Q.rear)
    {
        return false;
    }
    ret = Q.base[Q.front];
    Q.front = (Q.front + 1) % MaxSize;
    return true;
}

 

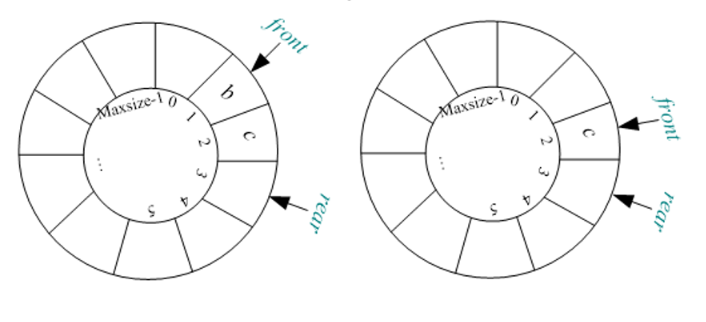
2.1.3.5 循环队列的队列长度

/*
    循环队列中到底存了多少个元素呢？循环队列中的内容实际上为Q.front到Q.rear-1这一区间的数据元素。
    Q.rear>=Q.front：  元素个数为Q.rear-Q.front；
    Q.rear<Q.front：    元素个数为Q.rear-Q.front+Maxsize；

    (Q.rear-Q.front+Maxsize) % MaxSize
*/
int QueueLength(SqQueue &Q)
{
    return (Q.rear - Q.front + MaxSize) % MaxSize;
}

 

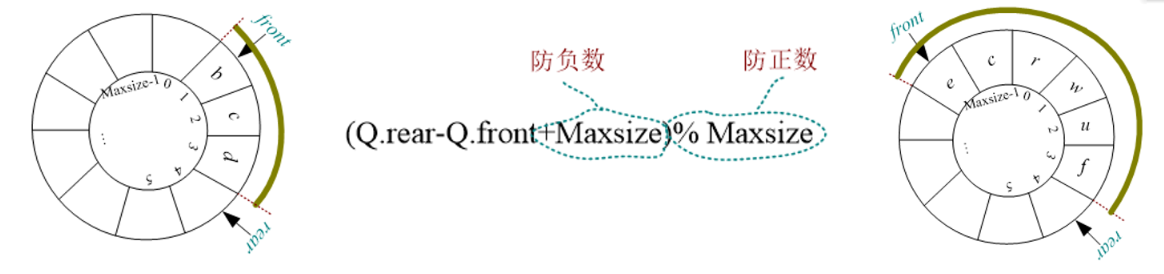
2.1.3.6 循环队列总结

队空: Q.front == Q.rear;                         // Q.rear 和 Q.front指向同一个位置
队满: (Q.rear+1)%MaxSize == Q.front;             // Q.rear 向后移一位正好是 Q.front
入队: 
     Q.base[Q.rear] = x;                        // 将元素 x 放入 Q.rear 所指向的空间
     Q.rear == (Q.rear+1) % MaxSize;            // Q.rear 向后移一位
出队: 
     e = Q.base[Q.front];                       // 用变量记录 Q.front 所指向的元素
     Q.front = (Q.front+1) % MaxSize;           // Q.front 向后移一位
队列中元素个数:       (Q.rear - Q.front + MaxSize) % MaxSize;

2.1.3.7 循环队列的算法时间复杂度

 

 

2.1.4 顺序队列（循环队列）的代码整合

 

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<string>
using namespace std;
#define MaxSize 100

typedef struct SqQueue
{
    int *base; // 基地址
    int front, rear;
}SqQueue;

// 循环队列初始化
bool InitQueue(SqQueue &Q)
{
    Q.base = new int[MaxSize];
    if (Q.base == NULL)
    {
        return false;
    }
    Q.front = Q.rear = 0;
    return true;
}

// 循环队列入队
bool EnQueue(SqQueue &Q, int value)
{
    if (((Q.rear + 1) % MaxSize) == Q.front)
    {
        return false;
    }
    Q.base[Q.rear] = value;
    Q.rear = (Q.rear + 1) % MaxSize;
    return true;
}

// 循环队列元素出队
bool DeQueue(SqQueue &Q, int &ret)
{
    if (Q.front == Q.rear)
    {
        return false;
    }
    ret = Q.base[Q.front];
    Q.front = (Q.front + 1) % MaxSize;
    return true;
}

// 获取循环队列的长度
int QueueLength(SqQueue &Q)
{
    return (Q.rear - Q.front + MaxSize) % MaxSize;
}

// 获取循环队列头节点
int GetHead(SqQueue &Q)
{
    if (Q.front == Q.rear)
    {
        return -1;
    }
    return Q.base[Q.front];
}


int main()
{
    SqQueue Q;
    int count, value, ret;
    cout << "初始化循环队列" << endl;
    if (InitQueue(Q))
    {
        cout << "循环队列初始化成功" << endl;
    }
    else
    {
        cout << "循环队列初始化失败" << endl;
        return -1;
    }
    cout << "请输入循环队列中的元素个数: ";
    cin >> count;
    for (int i = 1; i <= count; i++)
    {
        cout << "请输入第 " << i << " 个元素的值: ";
        cin >> value;
        if (EnQueue(Q, value))
        {
            cout << "循环队列的值 " << value << " 入队成功！" << endl;
        }
        else
        {
            cout << "队列已满，入队失败！" << endl;
        }
    }
    cout << "获取循环队列的长度: " << QueueLength(Q) << endl;
    while (true)
    {
        value = GetHead(Q);
        if ( value != -1)
        {
            cout << "循环队列的头结点是: " << value << endl;
        }
        
        if (DeQueue(Q, ret))
        {
            cout << "循环队列元素: " << ret << "出队！" << endl;
        }
        else
        {
            break;
        }
    }
    return EXIT_SUCCESS;
}

 

2.2 链式队列

2.2.1 链式队列的定义

typedef struct Qnode
{
    int data;
    struct Qnode *next;
}Qnode, *Qptr;

typedef struct
{
    Qnode *front;
    Qnode *front;
}LinkQueue;

 

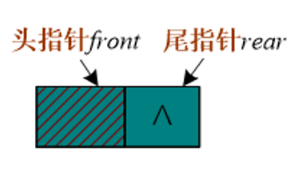
2.2.2 链式队列的初始化

/*
    链队的初始化，创建一个头结点，头指针和尾指针指向头结点。
*/
void InitQueue(LinkQueue &Q)
{
    Q.front = Q.rear = new Qnode;
    Q.front->next = NULL;
}

 

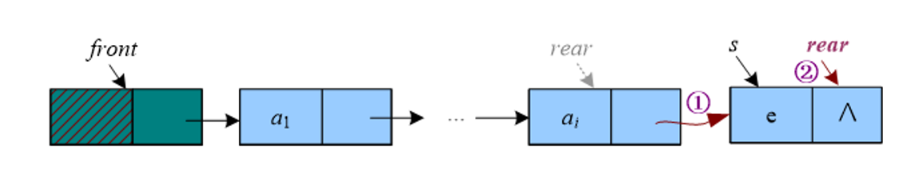
2.2.3 链式队列的入队

/*
    先创建一个新结点，将元素e存入该结点的数值域，然后将新结点插入队尾，尾指针后移。
*/
void EnQueue(LinkQueue &Q, int value)
{
    Qptr s = new Qnode;   
    s->data = e;
    s->next = NULL;
    Q.rear->next = s;
    Q.rear = s;      // 修改尾指针指向 s
}

 

2.2.4 链式队列的出队

/*
    出队相当于删除第一个数据元素，即将第一个数据元素结点跳过去，首先用p指针指向第一个数据结点，然后跳过该结点，若队列中只有一个元素，删除后需要修改队尾指针。
*/
bool DeQueue(LinkQueue &Q, int &ret)
{
    Qptr p;
    if(Q.front == Q.rear)
    {
        return false;
    }
    p = Q.front->next;
    ret = p->data;
    Q.fornt->next = p->next;
    if(Q.rear == p)
    {
        Q.rear = Q.front;
    }
    delete p;
    return true;
   
}

 

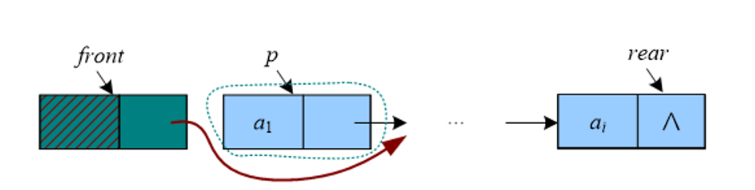
2.2.5 练市队列的取队头元素

/*
    队头实际上是Q.front->next指向的结点，即第一个数据结点，队头元素就是将该结点的数据域存储的元素。
*/
int FetHead(LinkQueue &Q)
{
    if(Q.front == Q.rear)
    {
        return -1;
    }
    return Q.front->next->data;
}

 

2.2.6 链式队列的算法时间复杂度

2.2.7 链式队列的代码整合

 

#define _CRT_SECURE_NO_WARNINGS 1
#include<iostream>
#include<string>
using namespace std;

typedef struct Qnode
{
    int data;
    struct Qnode *next;
}Qnode, *Qptr;

typedef struct
{
    Qnode *front;
    Qnode *rear;
}LinkQueue;

// 链式队列初始化
bool InitQueue(LinkQueue &Q)
{
    Q.front = new Qnode;
    Q.rear = Q.front;  // 创建头结点，头指针和尾指针指向头结点
    Q.front->next = NULL;
    return true;
}

// 链式队列入队
bool EnQueue(LinkQueue &Q, int value)
{
    Qptr s;
    s = new Qnode;
    s->data = value;
    s->next = NULL;
    Q.rear->next = s;
    Q.rear = s;
    return true;
}

// 链式队列获取头元素
int GetHead(LinkQueue &Q)
{
    if (Q.front == Q.rear)
    {
        return -1;
    }
    return Q.front->next->data;
}

// 链式队列出队
bool DeQueue(LinkQueue &Q, int &ret)
{
    Qptr p;
    if (Q.front == Q.rear)
    {
        return false;
    }
    p = Q.front->next;
    ret = p->data;       //保存队头元素
    Q.front->next = p->next;
    if (Q.rear == p)
    {
        Q.rear = Q.front; // 若队列中只有一个元素，删除后需要修改队尾指针
    }
    delete p;
    return true;
}
int main()
{
    LinkQueue Q;
    int count, value, ret;
    cout << "初始化链式队列！" << endl;
    if (InitQueue(Q))
    {
        cout << "链式队列初始化成功！" << endl;
    }
    else
    {
        cout << "链式队列初始化失败！" << endl;
        return -1;
    }
    cout << "请输入链式队列中的元素个数: ";
    cin >> count;
    for (int i = 1; i <= count; i++)
    {
        cout << "请输入第 " << i << " 个元素的值: ";
        cin >> value;
        EnQueue(Q, value);
        cout << "链式队列的值 " << value << " 入队成功！" << endl;
    }
    ret = GetHead(Q);
    if (ret != -1)
    {
        cout << "对头元素是: "<< ret << endl;
    }
    while (true)
    {
        if (DeQueue(Q, ret))
        {
            cout << "链式队列出队元素: " << ret << "出队！" << endl;
        }
        else
        {
            break;
        }    
    }
    return EXIT_SUCCESS;
}