洛谷P5597 复读

洛谷P5597 复读

首先概括一下题意：文中给出三个指令L（命令机器人向当前节点的左子节点走）、R（命令机器人向当前节点的右子节点走）、U（命令机器人向当前节点的父亲节点走）以及一颗二叉树。初始状态，机器人在二叉树的根节点。当机器人处于二叉树的根节点时，不可以执行指令U， 但是机器人可以走向不存在的节点。现在需要找到一个指令集，使得机器人能够遍历二叉树中所有节点且指令集长度最短。

输入：该二叉树的前序遍历，由0123中的字符组成：

• 0：表示这是一个没有儿子的节点。
• 1：表示这是一个只有左子的节点。
• 2：表示这是一个只有右子的节点。
• 3：表示这是一个既有左子又有右子的节点。

输出：指令集的长度。

---

先根据输入，建立这颗二叉树。由于给出的是前序遍历方式，可以选择使用递归建树方式，先建立根节点然后建立左子树、右子树。根据位运算的性质，对每个节点的值（0,1,2,3）可以分别进行按位与操作判断是否有左、右子节点。

void build_tree(int& x, int& cnt) {
    int c = getchar() - 48;
    if (!x) {
        x = ++cnt;
    }
    if (c & 1) {
        build_tree(tree[x].l, cnt);
    }
    if (c & 2) {
        build_tree(tree[x].r, cnt);
    }
}

其中cnt是节点编号。当输入为31330002300时，在树建立完成后，是如下情况。

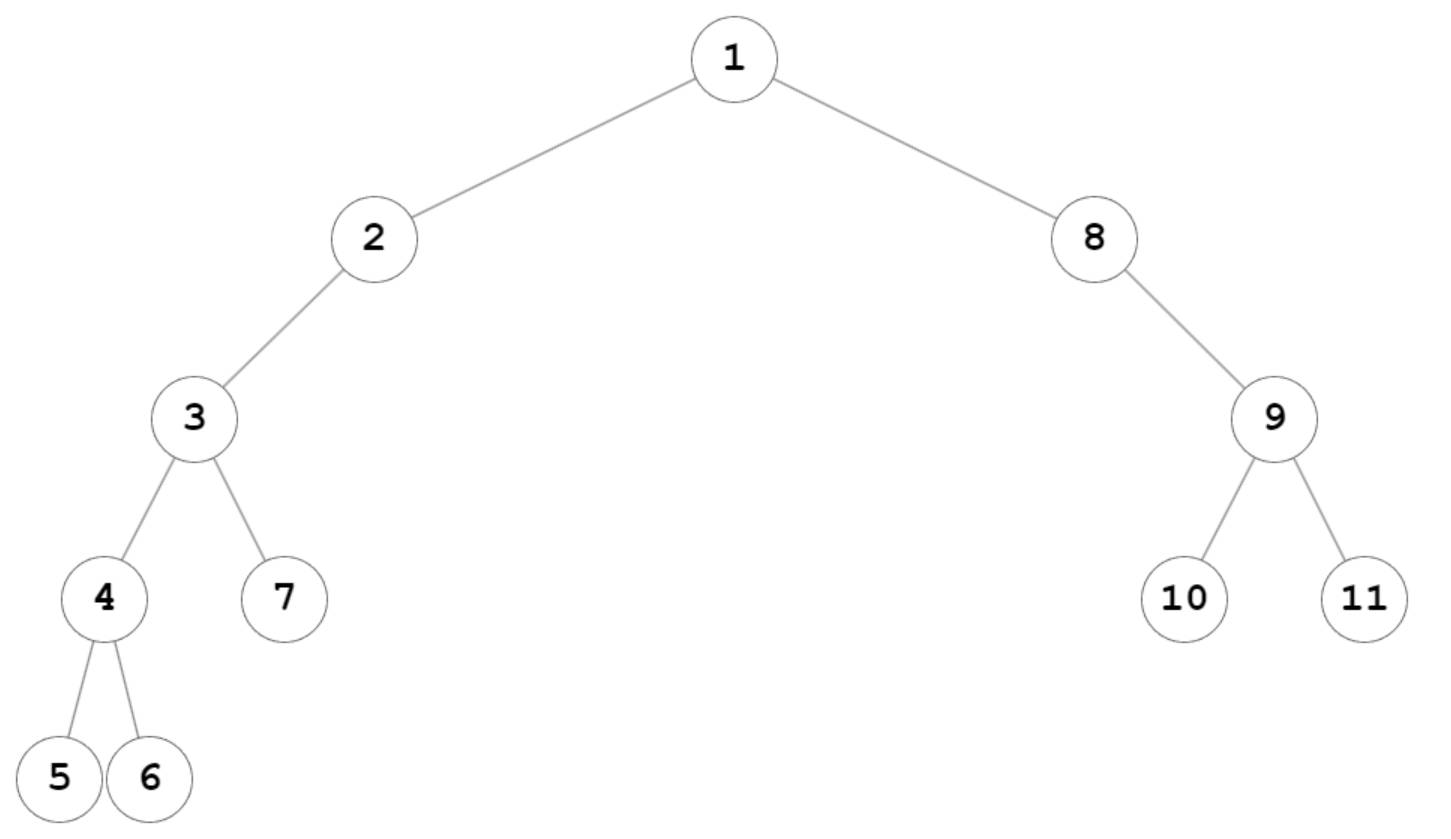
假设以编号为1的节点作为根节点建立一个无限大的完全二叉树，我们需要在执行若干次指令集后，遍历完1至11号节点。

将指令集记为\(C\)。假设在编号为\(1\)的节点执行了一次\(C\)后到达编号为\(3\)的结点，那么再执行一次\(C\)，他一定会到达编号为\(5\)的节点。也就是说每次执行指令集\(C\)，起点与终点的相对位置是完全相同的。随着指令集一直被不断地重复执行下去，到达的节点（不一定是否有编号，因为二叉树无限大）距离编号为\(1\)的节点的距离是越来越远的。所以在编号为\(1\)的节点执行了一次\(C\)后到达编号为\(3\)的结点后，此时\(1\)的右子树上所有的节点都必须被遍历到。如果没有被遍历到，那么下一次从编号为\(3\)的结点到编号为\(5\)的节点，在至以后，这些节点永远都不会被遍历到。

现在可以枚举执行一次指令集后所有可能的终点，也就是枚举所有的节点。根据上述的性质，建立另一颗二叉树。假设现在处于\(A\)节点执行一次指令集后到达\(B\)，再执行一次指令集后到达\(C\)。。。不妨以每次的起点为根节点，把不包含终点的子树的树截取下来，并将他们合并成一棵树。这颗合并树包含了一次指令集中需要遍历的所有节点。

如果这颗合并树共有\(n\)个节点，一次指令集的执行过程中可以发现，除起点到终点的边(边长也就是深度，记为\(deep\))走一遍外，其余的边均走两遍。所以指令集大小为\(2*(n-1)-deep\)。

合并树建立的过程和上述建树的过程类似，如果对应位置有节点就不做任何事情，如果没有节点（值为\(0\)）就新建节点，且节点编号为节点总数。

总体代码为

#include <climits>
#include <cmath>
#include <cstdio>
#include <cstring>
#include <deque>
#include <iostream>
#include <list>
#include <queue>
#include <sstream>
#include <stack>
#include <string>
#include <unordered_map>
#include <unordered_set>
#include <vector>

#define ULL unsigned long long
#define LL long long

using namespace std;

const int MAX = 2e3 + 50;
const int MOD = 1e4;

struct node {
    int l, r;
} tree[MAX], merge_shape_tree[MAX];

char pth[MAX];

void build_tree(int& x, int& cnt) {
    int c = getchar() - 48;
    if (!x) {
        x = ++cnt;
    }
    if (c & 1) {
        build_tree(tree[x].l, cnt);
    }
    if (c & 2) {
        build_tree(tree[x].r, cnt);
    }
}

void merge(int& x, int y, int& cnt, int& curr) {
    if (!x) {
        x = ++cnt;
    }
    // 当起点等于终点时，合并完成。
    if (y == curr) {
        return;
    }
    if (tree[y].l) {
        merge(merge_shape_tree[x].l, tree[y].l, cnt, curr);
    }
    if (tree[y].r) {
        merge(merge_shape_tree[x].r, tree[y].r, cnt, curr);
    }
}

void solve(int u, int deep, int& ans) {
    if (u != 1) {
        memset(merge_shape_tree, 0, sizeof(merge_shape_tree));
        int cnt = 1, curr = 1;
        while (curr) {
            int t = curr;
            for (int i = 0; i < deep; ++i) {
                // 根据pth[]，找到终点。
                curr = (pth[i] == 'l' ? tree[curr].l : tree[curr].r);
            }
            int root = 1;
            merge(root, t, cnt, curr);
        }
        ans = min(ans, (cnt - 1) * 2 - deep);
    }
    // 递归枚举所有节点作为终点，同时使用pth[]记录路径。
    pth[deep] = 'l';
    if (tree[u].l) {
        solve(tree[u].l, deep + 1, ans);
    }
    pth[deep] = 'r';
    if (tree[u].r) {
        solve(tree[u].r, deep + 1, ans);
    }
}

int main(int argc, char* argv[]) {
    
    int cnt = 1;
    int root = 1;
    build_tree(root, cnt);
    int ans = INT_MAX;
    solve(1, 0, ans);
    cout << ans << endl;

    return 0;
}