广度优先搜索——马的遍历

来自洛谷P1443 

整理b站up主嘉持的题解，还有参考up主旺仔老板_的讲解

 

题目描述

有一个n*m的棋盘(1<n,m<=400)，在某个点上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步

输入格式

一行四个数据，棋盘的大小和马的坐标

输出格式

一个n*m的矩阵，代表马到达某个点最少要走几步（左对齐，宽5格，不能到达则输出-1）

输入输出样例

输入：

3 3 1 1

 

输出：　

0    3    2    
3    -1   1    
2    1    4    

 

中国象棋中的马成“日”字走法，一个位置能有八个方向走法如图

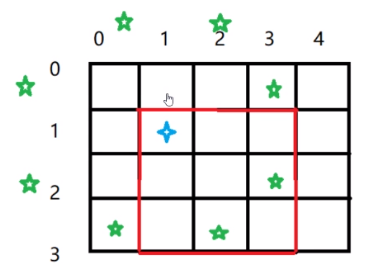
代码实现：

#include<iostream>
#include<queue>
#include<cstdio>
using namespace std;
const int N=410;
int n,m,sx,sy;
int map[N][N];//存放棋盘中每点到达步数，还有判重功能 
int dx[]={1,1,-1,-1,2,2,-2,-2};
int dy[]={2,-2,2,-2,1,-1,1,-1};//围棋马能走的八个方向 
/*或者开一个二维数组int dd[8][2]={{1,2}，{1，-2}，{-1,2}....}
dd[][0]就等于dx[]；dd[][1]就等于dy[] */ 
struct Node{
    int x;
    int y;
    int step;
};//将每个点的位置和达到所用步数打包成Node类型（结构体） 


int main(){
    cin>>n>>m>>sx>>sy;
    queue<Node>Q;//定义一个Node类型的队列 
    Q.push((Node){sx,sy,0});//将初始点信息压进队首
    /*也可以
    Node t;
    t.x=sx;t.y=sy;t.step=0;
    Q.push(t); 
    */ 
    
    for(int i=1;i<=n;i++){    
    for(int j=1;j<=m;j++)
        map[i][j]=-1;
    }//将棋盘步数都变成-1，走不到的点就会一直是-1 
    
        map[sx][sy]=0;//从初始点出发广搜，将初始点步数变成0 
        
    while(!Q.empty()){//bfs开始 
        for(int i=0;i<8;i++){//八个方向广搜 
            int xx=Q.front().x+dx[i];
            int yy=Q.front().y+dy[i];
            if(xx>=1&&xx<=n&&yy>=1&&yy<=m&&map[xx][yy]==-1)//如果搜到的点在棋盘里且没有被搜到过 
            {    Q.push((Node){xx,yy,Q.front().step+1});//将能走到的点压入队列 
                map[xx][yy]=Q.front().step+1;//步数更新 
             } 
        
        }
        Q.pop();//当队首的下一层可以走到的点全部放入队列后，队首踢出 
    }
    for(int i=1;i<=n;i++){//按格式输出 
    
        for(int j=1;j<=m;j++)
        printf("%-5d",map[i][j]);
        printf("\n");
    }
    
    return 0;
}