DQN算法

Q-Learning算法

输入：episodes \(T\)，状态集合 \(S\)，动作集合 \(A\)，步长 \(\alpha\)，衰减因子 \(\gamma\)，探索率 \(\epsilon\)
输出：所有状态和行为对应的 \(Q\) 值表

1. 随机初始化 \(Q\) 值表，终止状态所对应的 \(Q\) 值设为0
2. for i from 1 to T:
   a. 随机选择初始化状态 \(S_t\)
   b. 基于 \(Q\) 值表，使用 \(\epsilon\) 贪婪法选择动作 \(A_t\)，得到即时奖励 \(R_t\)，进入下一状态 \(S_{t+1}\)
   c. 更新 \(Q\) 值表： \(Q(S_t, A_t) = Q(S_t, A_t) + \alpha (R_t + \gamma \max_{a}{Q(S_{t+1}, a}) - Q(S_t, A_t))\)
   d. 如果 \(S_{t+1}\) 是终止状态，该轮迭代完毕，否则转移到步骤 b

DQN算法

当问题的状态集合非常大的时候，使用Q值表不太现实，一个可行的方法是对价值函数进行近似表示。比如引入一个状态价值函数\(v\)，该函数由参数\(w\)表示，接收状态\(s\)作为输入，我们希望：\(v(s;w) \approx v_\pi(s)\)；又比如引入一个行为价值函数\(q\)，函数同样由参数\(w\)表示，接收状态\(s\)和行为\(a\)作为输入，我们希望：\(q(s,a;w) \approx q_\pi(s,a)\).

DQN网络的输入是state，输出是所有action在该状态下的action-value。DQN的主要技巧是经验回放，也就是将每次和环境交互得到的奖励与状态更新情况保存起来（即一个五元组），用于后面目标Q值的更新（在Q-learning中有Q值表保存当前结果，而DQN没有，所以需要经验回放）。

算法过程为：

初始时，我们是搭建两个相同的网络，分别称为评估网络和目标网络。对于每个episode，设置初始状态：

• 1.将状态送入评估网络得到所有action对应的Q值，根据epsilon-greedy方法选择action。
• 2.在当前状态执行action得到奖励和下一状态\(S_{t+1}\)等，将五元组放到经验集合中。
• 3.训练：每达到一定步长，将评估网络的参数赋值给目标网络。从经验集合采取batch size个样本，训练方法为，将batch个样本的states送入评估网络，在网络输出结果中提取样本中actions所对应的Q值（评估值），使用图中公式计算目标值（需要使用目标网络来计算下一状态下的最大Q值）。计算评估值与目标值的loss，反向传播更新评估网络。
• 4.如果\(S_{t+1}\)为终止状态，则停止该轮迭代，否则回到1

Double DQN

在DQN中，目标值虽然是使用目标网络来计算，但仍然是使用贪婪法得到的，即：

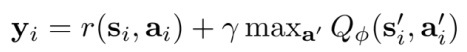
为了避免过度估计的问题，我们解耦目标值动作的选择和目标值的计算这两步，即不再直接在目标网络里面找各个动作中最大Q值，而是先在评估网络中找出最大Q值对应的动作，然后利用这个选择出来的动作在目标网络里面去计算目标值，即：

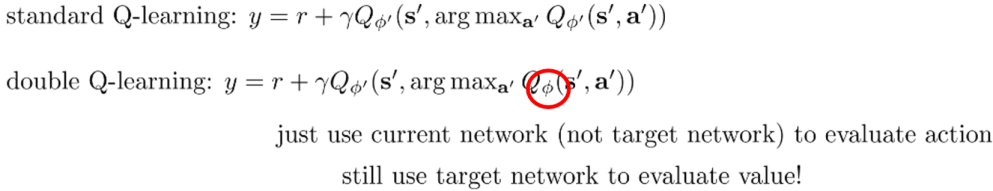
Dueling DQN

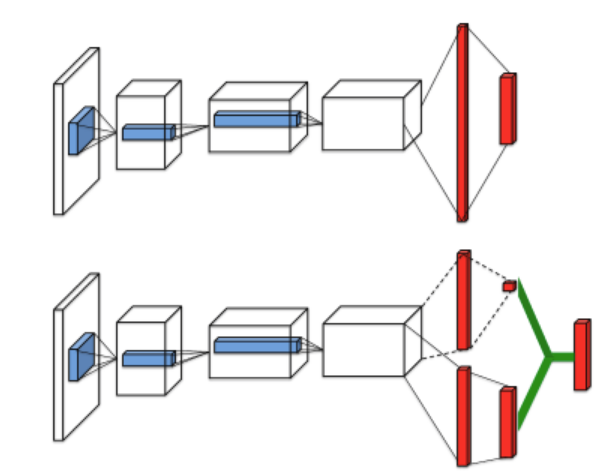
Dueling DQN将Q网络分为两部分：第一部分仅仅与状态\(s\)有关，与具体要采用的动作\(a\)无关，这部分称为价值函数，记为\(V(s;w,\alpha)\)；第二部分同时与状态\(s\)和动作\(a\)有关，这部分称为优势函数，记为\(A(s,a;w,\beta)\)，最终价值函数表示为：$$Q(s,a;w,\alpha,\beta) = V(s;w,\alpha) + A(s,a;w,\beta)$$
其中\(w\)是公共部分的网络参数，\(\alpha\)是价值函数独有部分的网络参数，而\(\beta\)是优势函数独有部分的网络参数。