洛谷2022年十二月月赛题解

T1

只有第一秒走的长度为奇数，后面每一秒走的长度都为偶数，因此所有除 \(0\) 外的偶数点都是不可达的。

当 \(n\) 为奇数时，设 \(d\) 为满足 \(\sum\limits_{i=1}^d 2^{i-1}\ge n\) 的最小值。可以证明答案为 \(d\)。

证明：

初始令每一秒都是往右走的，我们需要将某一些秒调整为往左走使得最终恰好走到 \(n\)。

设 \(m=\sum\limits_{i=1}^d 2^{i-1}-n\)。显然 \(m\) 为偶数。

我们需要找到一些秒，使得这些秒中走的距离之和恰好为 \(\dfrac{m}{2}\)，并将这些秒调整为往左走。

只需要找出 \(\dfrac{m}{2}\) 的二进制表示，将它分解为若干个互不相同的 \(2\) 的幂之和，这样就一定可以得到一组方案。

时间复杂度 \(O(T)\) 或 \(O(T\log n)\)。

T2

Subtasks 1 and 2

Subtask 1 直接枚举每条消息是否撤回，然后 \(O(m)\) 判断一下，时间复杂度 \(O(m2^m)\)。

首先我们考虑一件事，撤回别人的消息好还是自己的消息好。

如果你撤回一条别人的消息 \(A\)，在 \(A\) 之后第一条自己的消息是 \(B\)，那么：

• 如果撤回 \(A\)，那么消息 \(B\) 排名减 \(1\)，还可能导致惩罚；同时 \(B\) 之后的消息排名减 \(1\)。
• 如果撤回 \(B\)，那么它不可能造成惩罚，之后的消息排名仍然减 \(1\)。

因此，撤回别人的消息总是不优于撤回自己的。

枚举每条自己的消息是否撤回，然后判断一下，时间复杂度 \(O(n2^n+m)\)。

Subtask 3

我们发现，是否撤回后面的消息，不影响前面消息的排名。

因此，如果前面的消息都已经决定是否撤回，那么当前消息如果会导致惩罚就删掉，否则不删掉。

如果删掉一条消息，那么之后的消息排名要全部减 \(1\)，时间复杂度 \(O(n^2+m)\)。

Subtask 4

每条消息都是小 A 发的。不管他删多少条消息，总是占据消息记录的前若干条。

因此，最多留几条消息，相当于 \(f\) 有几个前缀 \(0\)。

Subtasks 5 and 6

在 Subtask 3 基础上，不实时更新每条消息的排名，而是需要决策时，它之前撤回几条消息，排名就减去几。

时间复杂度 \(O(n+m)\)，常数极小。

T3

结论 \(1\)：一定存在一种最优方案，满足 \(c\) 单调不降。

证明：反证，如果存在 \(i<j\) 满足 \(c_i>c_j\)，我们可以交换 \(c_i,c_j\)，显然满足条件且方差不变。

结论 \(2\)：一定存在一种最优方案，满足存在一个 \(i\)，使得 \(c_{1\dots i-1}=a_{1\dots i-1},c_{i+1\dots n}=b_{i+1\dots n}\)。

证明：反证，如果存在 \(i<j\) 满足 \(c_i>a_i\) 且 \(c_j<b_j\)，那么可以 \(c_i\leftarrow c_i-1,c_j\leftarrow c_j+1\)，显然方差增大。

结论 \(3\)：一定存在一种最优方案，满足存在一个 \(i\)，使得 \(c_{1\dots i}=a_{1\dots i},c_{i+1\dots n}=b_{i+1\dots n}\)。

根据结论 \(2\)，我们得到了一个位置 \(j\)，此时 \(c\) 中除了 \(c_{j}\) 都已经确定下来了，此时方差是一个关于 \(c_j\) 的二次函数。可以发现这个二次函数是下凸的，因此取到最大值时一定有 \(c_j=a_j\) 或 \(c_j=b_j\)。所以 \(i=j\) 或 \(i=j-1\)。

有了结论 \(3\)，我们只需要枚举其中的 \(i\) 即可得到答案。时间复杂度 \(O(n)\)。

T4

当 \(n\) 为奇数时显然不存在答案。考虑偶数怎么做。

当 \(n=4\) 时容易构造出方案，接下来考虑如果每次增加两个点，我们应该怎么加边，才能维护生成树的性质。

如果我们在原来基础上连续添加一对相邻三角形（左图，增加 \(0,2\) 两点），那么可以添加 \((0,4),(2,4)\) 两条边；如果在相邻两条边上各加入一个三角形（右图，增加 \(1,2\) 两点），那么可以添加 \((0,1),(0,2)\) 两条边。

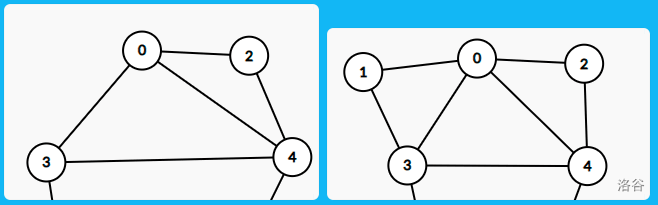
接下来需要证明所有 \(n\) 为偶数的三角剖分都可以用这两种方法得到。

如果我们以每个三角形为结点，相邻三角形间连边，那么每个点度数不超过 \(3\)，是一棵二叉树。

如果我们要给树 \(T\) 构造答案，那么：

• 如果 \(T\) 的两个孩子都有偶数个三角形，则分别让两个孩子自给自足即可，根等待父亲连边。
• 如果 \(T\) 两个孩子都有奇数个三角形，则我们用上面右图的方法连接两个孩子。
• 如果 \(T\) 两个孩子一奇一偶，则根应该和奇数子树的根使用左图方法连接。

这样整棵树 \(T\) 都能被构造一个合法的答案。

T5

称一个好区域是极大的当且仅当它的边界上至少有 \(3\) 个点。有结论：一定存在一组最优解，使得它是一个极大好区域。不妨设是左，右，下边界上有点。

枚举下边界上的点，有结论：最多只有一个合法的极大好区域。

也就是说，可能成为答案的极大好区域只有 \(O(n)\) 个。

考虑怎么找到一个点 \((x,y)\) 对应的极大好区域。

我们可以考虑钦定这个区域的边长 \(l\)，分别找到左右两边第一个纵坐标在 \((y,y+l)\) 内的点，设为 \((x_1,y_1),(x_2,y_2)\)。

二分出最大的 \(l\) 满足 \(x_2-x_1\ge l\)。如果 \(x_2-x_1=l\) 则我们已经求出了极大好区域，否则要么不存在极大好区域，要么存在一个纵坐标为 \(y+l\) 的点在极大好区域的角上，找到这个点即可求出极大好区域。可以在主席树上二分，时间复杂度 \(O(n\log n)\)。

这里有一个减小常数的方法：没有必要对四个方向各做一遍，只需要做 左右上 和 左右下 这两种情况即可，可以证明这样不会漏掉任何极大好区域。

求出这 \(O(n)\) 个极大好区域之后，可以考虑用扫描线 + 线段树求出答案。一般的做法是对于每个节点维护一个 set，其中包含当前覆盖这个节点的所有正方形。这样做的时间复杂度是 \(O(n\log^2 n)\)。

但实际上我们可以利用正方形的性质进行优化。对于每个节点，如果其中有两个正方形 \(S_1,S_2\) 满足 \(|S_1|>|S_2|\) 且 \(S_1\) 的右边界在 \(S_2\) 的右边界的右侧，那么显然 \(S_2\) 就没用了。

因此我们可以对于每个节点维护一个 deque，里面包含当前覆盖这个节点并且有用的正方形。这个 deque 中的所有正方形满足边长单调递减，且右边界的位置单调递增。加入一个新的正方形时边长比它小的正方形显然都没用了，直接从末尾弹出即可，然后再判断它本身是否有用即可。时间复杂度均摊 \(O(n\log n)\)。

因此总时间复杂度为 \(O(n\log n)\)，常数很大。

T6

先考虑给定 \(a\) 怎么算出答案。

设 \(f_{i,j}\) 表示当前考虑到 \(i\)，且 \(b_i=j\) 的答案。

\[f_{i,j}=\min\limits_{k\le j}\{f_{i-1,k}\}+|a_i-j| \]

发现对于每一个 \(i\) 的所有 \(dp\) 值都是一个下凸函数，那么可以考虑一个经典套路：用堆维护所有斜率增加 \(1\) 的断点。

同时设 \(mn_i=\min\{f_{i,j}\}\)。

每次操作相当于是往堆中先加入两个 \(a_i\) 然后弹出最大值 \(mx\)，可以发现 \(mn_i=mn_{i-1}+mx-a_i\)。

去掉一些可以快速计算的东西之后，我们实际上只需要考虑过程结束时堆中剩下的数之和。

我们考虑拆开每个数的贡献。具体地，钦定一个 \(x\in [0,m]\)，并把 \(\le x\) 的数设为 \(0\)，\(>x\) 的数设为 \(1\)。

现在只需要对所有 \(x\) 算出答案之和即可。

对于一个 \(x\)，设 \(g_{i,j}\) 表示当前考虑到 \(i\)，当前堆中有 \(j\) 个 \(1\) 的方案数。

每次操作有 \(x\) 种方案减少一个 \(1\)，有 \(m-x\) 种方案增加一个 \(1\)。特别地，任意时刻 \(1\) 的个数会对 \(0\) 取 \(\max\)。

可以发现，每一个 \(g_{i,j}\) 都是一个关于 \(x\) 的不超过 \(n\) 次的多项式，直接暴力维护这些多项式即可做到 \(O(n^3)\) 的复杂度。

但这还不够，我们需要进一步优化这个算法。

考虑把这个问题转化为格路计数。

对于一条当前意义下的路径，每次找到第一个对 \(0\) 取 \(\max\) 的位置并把它前面的部分全部往上平移一格。

这样我们就把对 \(0\) 取 \(\max\) 的要求去掉了。可以发现这两种路径是一一对应关系。

此时问题转化为了：

• 起点为横坐标为 \(0\) 的任意一个点。
• 每次有 \(x\) 种方案往右下，有 \(m-x\) 种方案往右上走。
• 终点为横坐标为 \(n\) 的任意一个点。
• 路径上所有点纵坐标都 \(\ge 0\) 且至少有一个点纵坐标为 \(0\)。

设走到 \((n,i)\) 的方案数为 \(w_i\)。我们要求的是 \(\sum\limits_i i\times w_i\)。

路径上至少有一个点纵坐标为 \(0\) 这个限制比较麻烦，我们将其容斥掉。

令 \(w_i=w_{0,i}-w_{1,i}\)，其中 \(w_0\) 和 \(w_1\) 分别描述纵坐标都 \(\ge 0\) 和纵坐标都 \(\ge 1\) 的情况。

根据经典的反射容斥方法可以得到：

\[w_{0,i}=\sum\limits_{i+2j\ge n}x^j(m-x)^{n-j}\left(\dbinom{n}{j}-\dbinom{n}{i+j+1}\right) \]

\[w_{1,i}=\sum\limits_{i+2j\ge n}x^j(m-x)^{n-j}\left(\dbinom{n}{j}-\dbinom{n}{i+j}\right) \]

\[w_i=w_{0,i}-w_{1,i}=\sum\limits_{i+2j\ge n}x^j(m-x)^{n-j}\left(\dbinom{n}{i+j}-\dbinom{n}{i+j+1}\right) \]

代回我们要求的式子里可以得到：

\[\sum\limits_{i\ge 0} w_i\times i=\sum\limits_{i\ge 0} i\sum\limits_{i+2j\ge n}x^j(m-x)^{n-j}\left(\dbinom{n}{i+j}-\dbinom{n}{i+j+1}\right) \]

\[=\sum\limits_{i\ge 0} x^i(m-x)^{n-i}\sum\limits_{j\ge\max\{i,n-i\}} (j-i)\left(\dbinom{n}{j}-\dbinom{n}{j+1}\right) \]

推到这里，我们已经可以非常简单地在 \(O(n^2)\) 的时间复杂度内求出这个多项式。

再用你喜欢的方式求出自然数幂和带进多项式计算，时间复杂度 \(O(n^2)\)。

进一步地，可以用卷积求出这个多项式，然后将自然数幂和代入计算。时间复杂度 \(O(n\log n)\)。