洛谷P9961 [THUPC 2024 初赛] 排序大师 题解

题目链接

这个题太牛了!!!

想题过程

是完全想不到的转化题意题.

这个题第一眼看上去感觉很像区间dp,试了一下发现这个修改操作还是太灵活了,无法进行限制,于是转战贪心.

这时想到一个结论,前缀已经排好序的我们不会动,肯定不优,所以考虑到去找第一个没有排好序的数,这个数我们一定要用一次包含它的操作去把它挪走.

事实证明这个结论是对的,但是没用

接着考虑转化题意一类的东西,一般是建图啥的,但是这个是真完全没有思路,遂开题解.

题解部分

考虑建图,这个建图的方式有两个要求

1. 每次交换操作只能修改常数次(点或边)
2. 最后的终止状态要简洁,且尽量是唯一的

最神仙的一步 : 添加两个数 \(a_0=0,\ a_{n+1}=n+1\) ,并将 \(a_i+1 \rightarrow a_{i+1}\;(0\le i \le n)\)

此时我们发现,终止状态会形成 \(n\) 个自环

而因为只有 \(n\) 条边,所以状态是唯一的.

下面我们考虑一次操作会带来哪些影响.

在上图中,我们发现每次操作会做交换两个点的出边的操作两次,而如果这两个点的出边在一个环上,那么就会将其断开,变成两个环.

于是我们发现一次操作最多能增加两个环.

这时聪明的小朋友就要问了,要是 \(j+1 = l\) 怎么办呢.

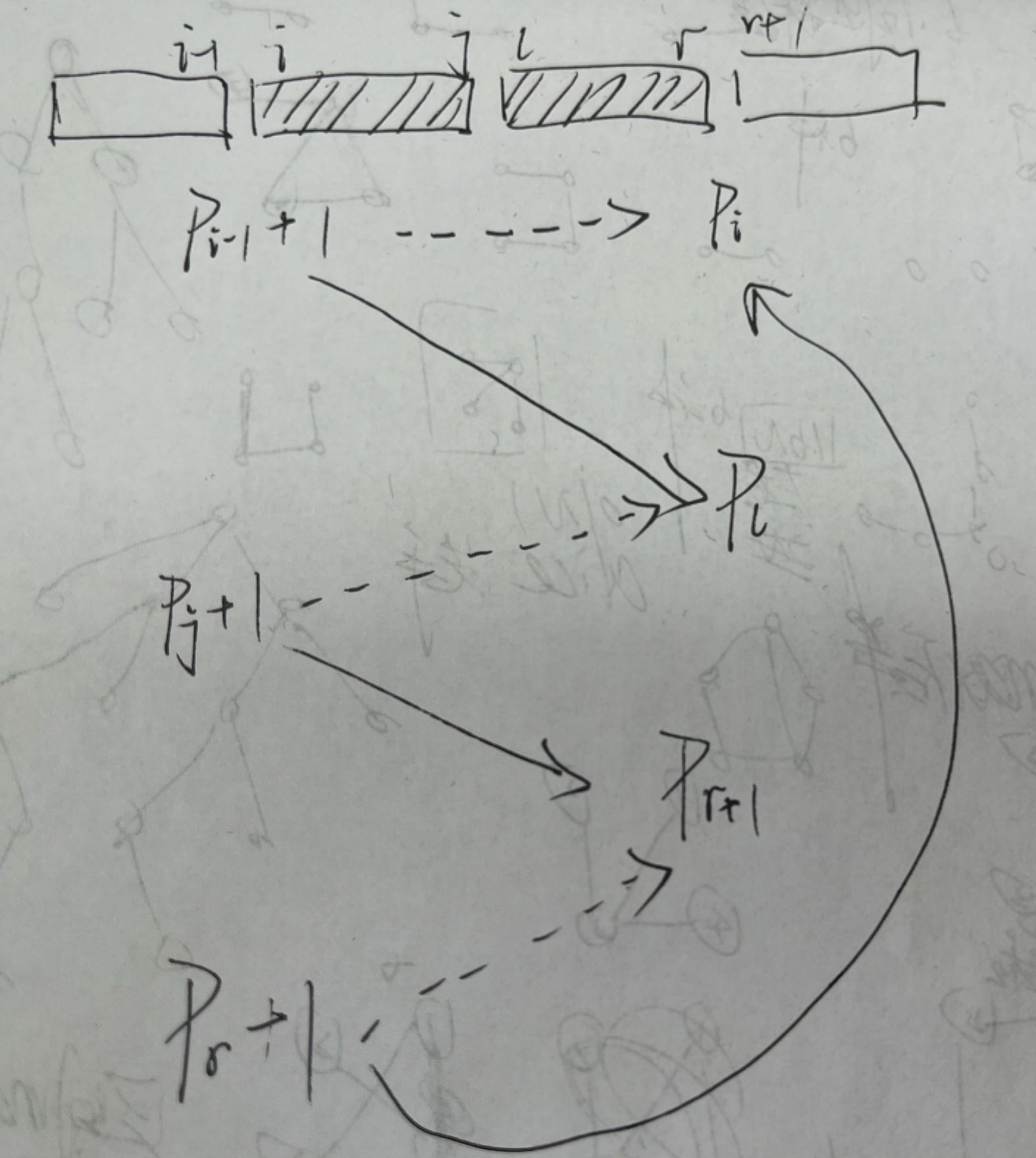
我们可以把它看做,先交换上面两个,再交换下面两个,仍然是两次交换.

现在我们只需要构造一种方式,使得每次交换都能取到上界即可.

具体的,我们找到 \(x\) ,定义为整个序列中,前面有比它大的数的值最小的数.

再找到 \(y\) , 定义为 \(x\) 前面最大的数.

此时 \(x-1\) 必定在 \(y\) 前面,不然不符合 \(x\) 的定义.

此时 \(y+1\) 必定在 \(x\) 后面,不然不符合 \(y\) 的定义.

我们交换区间 \([p_{x-1}+1,p_y]\) 与 \([p_x,p_{y+1}-1]\)

\(p_i\) 定义为值为 i 的数字出现的位置

手模一下发现,此时这两个区间交换后,被交换的出边必定在一个环上(因为两对出边分别都与 \(x\) 和 \(y\) 相邻).

至此,这道题被解决了.

点击查看代码

#include<bits/stdc++.h>
#define ll long long
#define F(x,y,z) for(int x=(y);x<=(z);x++)
using namespace std;
const int N=2010;
int n,a[N],b[N];
struct node{
    int l,r,i,j;
};
vector <node> ans;
void work(int l,int r,int i,int j){
    ans.push_back(node{l,r,i,j});
    int m=0;
    for(int k=1;k<l;k++) b[++m]=a[k];
    for(int k=i;k<=j;k++) b[++m]=a[k];
    for(int k=r+1;k<i;k++) b[++m]=a[k];
    for(int k=l;k<=r;k++) b[++m]=a[k];
    for(int k=j+1;k<=n;k++) b[++m]=a[k];
    for(int k=1;k<=n;k++) a[k]=b[k];
}
int main(){
    ios::sync_with_stdio(false);
    cin.tie(0);cout.tie(0);
    cin>>n;
    for(int i=1;i<=n;i++) cin>>a[i];
    int now=1;
    a[0]=0;a[n+1]=n+1;
    while(1){
        while(now<=n && a[now]==now) now++;
        if(now>n) break;
        int y=0,x=0;
        for(int l=now;l<=n;l++){
            if(y==0) y=l;
            else{
                if(a[y]>a[l]){
                    if(!x || a[x]>a[l]) x=l;
                }
                else y=l;
            }
        }
        y=0;
        for(int i=now;i<x;i++) if(!y || a[y]<a[i]) y=i;
        int l,r;
        // cout<<now<<endl;
        for(int i=0;i<=x;i++) if(a[i]==a[x]-1) l=i;
        for(int i=x;i<=n+1;i++) if(a[i]==a[y]+1) r=i;
        // cout<<l<<' '<<y<<' '<<x<<' '<<r<<endl;
        // return 0;
        work(l+1,y,x,r-1);
        // for(int i=1;i<=n;i++) cout<<a[i]<<' ';
        // cout<<endl;
        // return 0;
    }
    cout<<ans.size()<<'\n';
    for(auto y:ans) cout<<y.l<<' '<<y.r<<' '<<y.i<<' '<<y.j<<'\n';
    return 0;
}