关于矩阵快速幂

矩阵快速幂，顾名思义，是将快速幂算法运用到矩阵中，已达到时间优化的目的。

先来康康快速幂算法。

如果要求解x的n次方，例如7的10次方，当我们用pow函数时要进行10次计算，但当我们把10二进制化，即为（1010），则该计算结果可化为7的（1000）次方乘以7的（10）次方，即7的8次方乘7的平方，7的8次方可以经过7的平方乘以7的平方得到7的四次方，然后7的四次方乘以7的四次方得到7的八次方，总共只需要四次计算即可算出7的10次方，起到了减少计算次数的目的。

那么快速幂的模板如下：

int qpow(int m, int n)//m为底数，n为指数
{
int ans = 1;
while (n)
{
if (n & 1) ans = ans * m;//判断m是奇数还是偶数，即m转化为二进制后最低位是1还是0
m = m * m;
n >>= 1;//m的二进制数右移一位
}
return ans;
}

 

矩阵的快速幂原理是一样的，下面用三个例题来说明一下。（往往用到矩阵快速幂的题目的难点在于矩阵的构造）

首先是矩阵快速幂，可以记为模板https://www.luogu.com.cn/problem/P3390

AC代码如下：

#include<iostream>
using namespace std;
const int N = 110;
typedef long long ll;
struct mat
{
    ll m[N][N];
};
mat a, b,c,ans;
ll n, m;
mat mul(mat a, mat b)
{
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            c.m[i][j] = 0;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            for (int k = 0; k < n; k++)
                c.m[i][j] = c.m[i][j]%(1000000007)+a.m[i][k]*b.m[k][j]%(1000000007);//矩阵乘法
    return c;
}
void qpow(mat a, ll m)
{
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            ans.m[i][j] = 0;
    for(int i=0;i<n;i++) ans.m[i][i]=1;
    while (m)
    {
        if (m & 1) ans = mul(a, ans);
        a = mul(a, a);
        m >>= 1;
    }
}//将快速幂运用于矩阵
int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            cin >> a.m[i][j];
    qpow(a, m);
    for (int i = 0; i < n; i++)
    {
        for (int j = 0; j < n; j++)
        {
            cout << ans.m[i][j]%(1000000007) << ' ';
        }
        cout << endl;
    }
}

 

 

第二题是斐波那契数列。https://www.luogu.com.cn/problem/P1962

矩阵构造过程如下：

 

 

 

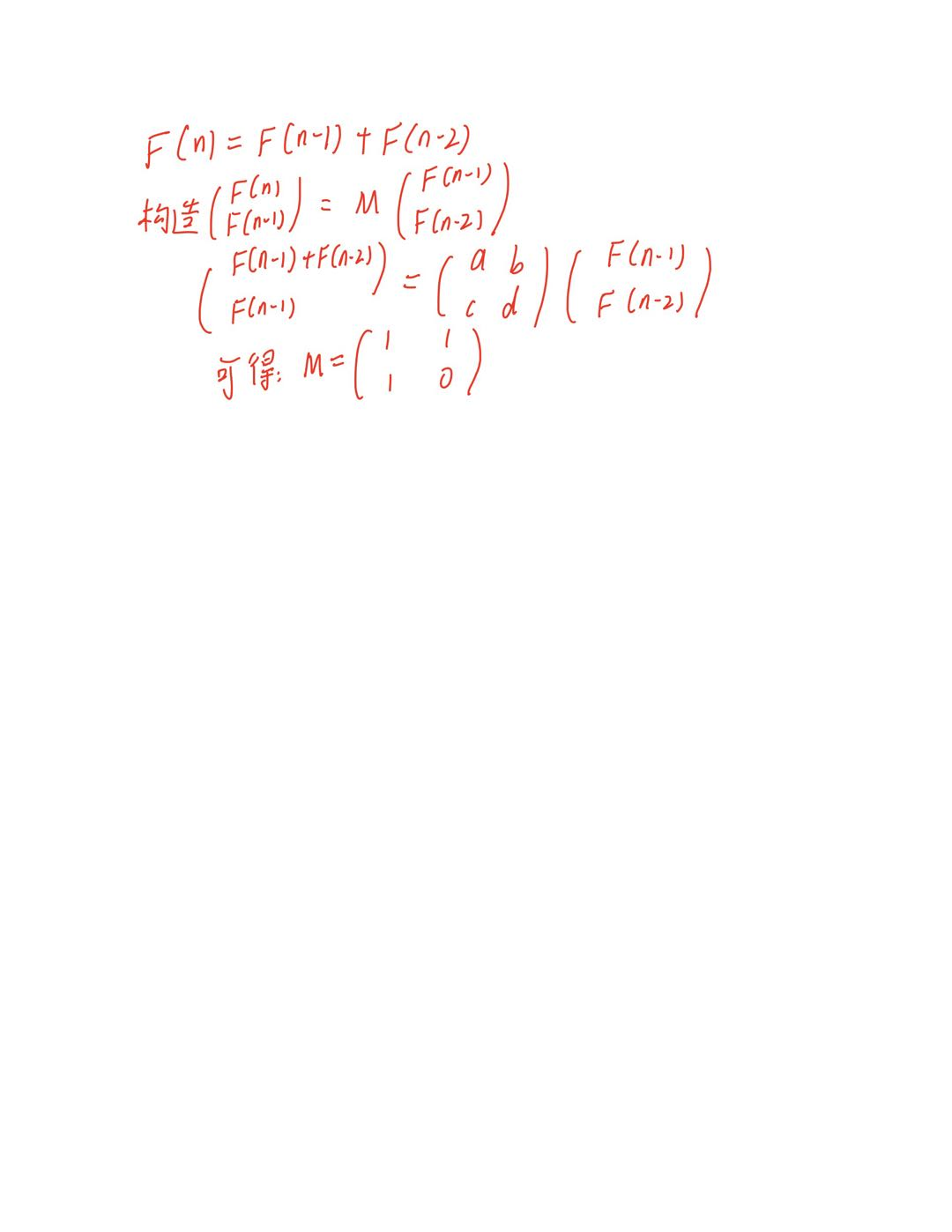
AC代码实现如下：

#include<iostream>
using namespace std;
typedef long long ll;
ll mod=1000000007;;
struct mat
{
    ll m[100][100];
};
mat a,c, ans;
mat mul(mat a, mat b)
{
    for(int i=0;i<2;i++)
    for(int j=0;j<2;j++)
    c.m[i][j]=0;
    for (int i = 0; i < 2; i++)
        for (int j = 0; j < 2; j++)
            for (int k = 0; k < 2; k++)
                c.m[i][j] =c.m[i][j]%mod+(a.m[i][k] * b.m[k][j])%mod;
    return c;
}
mat qpow(mat a, ll n)
{
    for (int i = 0; i < 2; i++)
        for (int j = 0; j < 2; j++)
            ans.m[i][j] = 0;
    for (int i = 0; i <2; i++) ans.m[i][i] = 1;
    while (n)
    {
        if (n & 1) ans = mul(ans, a);
        a = mul(a, a);
        n >>= 1;
    }
    return ans;
}
int main()
{
    cin.tie(0);
    cout.tie(0);
    ll num;
    cin >> num;
    a.m[0][0] = a.m[0][1] = a.m[1][0] = 1;
    a.m[1][1] = 0;
    mat aw=qpow(a,num-1);
    if(num>=3) cout << aw.m[0][0]%mod << endl;
    else cout<<1<<endl;
    return 0;

}

第三题.POJ3233  Given a n × n matrix A and a positive integer k, find the sum S = A + A² + A³ + … + A^k.

矩阵推导过程如下：

 

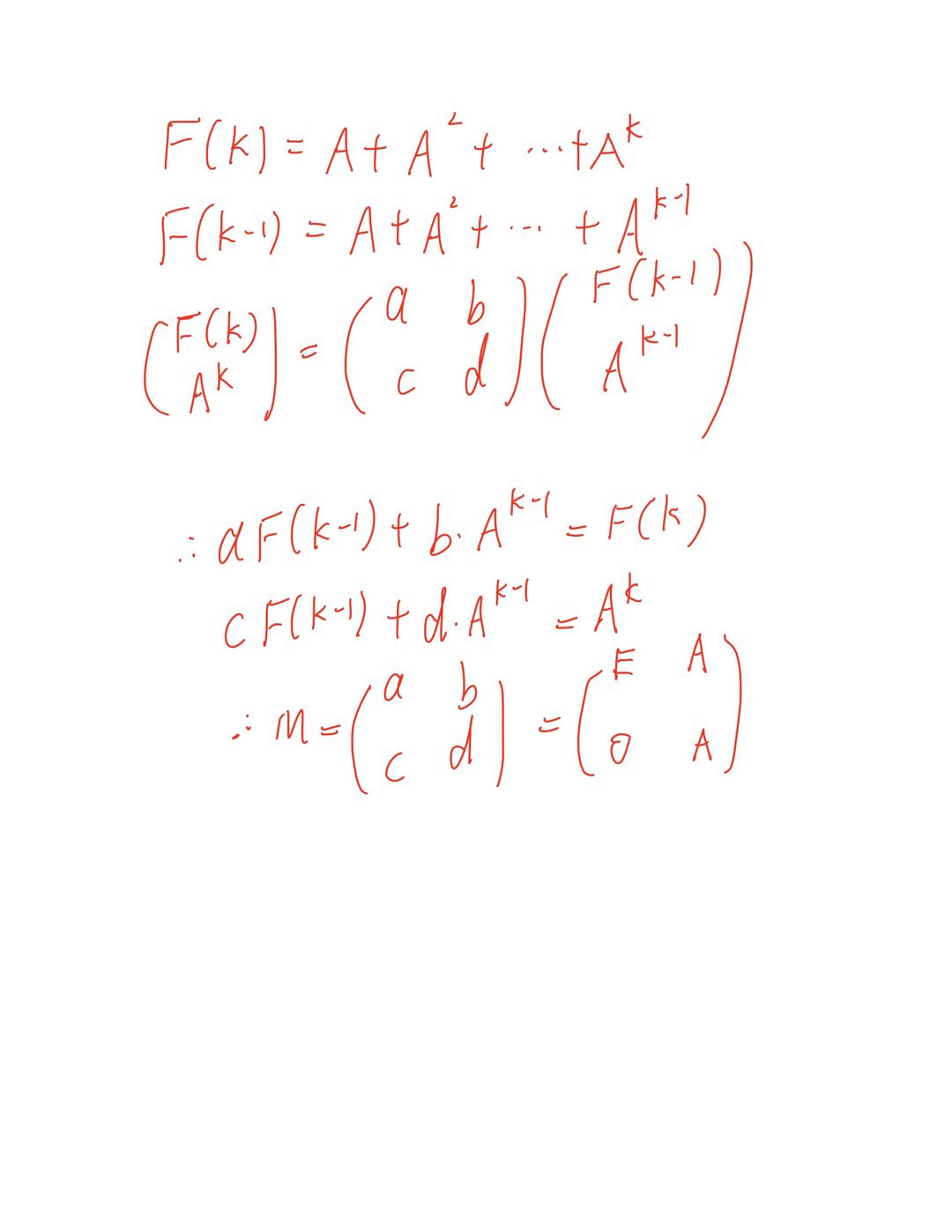
 AC代码如下：

#include<iostream>
using namespace std;
const int N = 110;
typedef long long ll;
struct mat
{
    ll m[N][N];
};
mat a, b,c,ans;
ll n, m,k;
mat mul(mat a, mat b)
{
    for (int i = 0; i < 2*n; i++)
        for (int j = 0; j < 2*n; j++)
            c.m[i][j] = 0;
    for (int i = 0; i < 2*n; i++)
        for (int j = 0; j < 2*n; j++)
            for (int k = 0; k < 2*n; k++)
                c.m[i][j] = c.m[i][j]%m+a.m[i][k]*b.m[k][j]%m;
    return c;
}
void qpow(mat a, int m)
{
    for (int i = 0; i < 2*n; i++)
        for (int j = 0; j < 2*n; j++)
            ans.m[i][j] = 0;
    for(int i=0;i<2*n;i++) ans.m[i][i]=1;
    while (m)
    {
        if (m & 1) ans = mul(a, ans);
        a = mul(a, a);
        m >>= 1;
    }
}
int main()
{
    cin>>n>>k>>m;
    for(int i=0;i<n;i++)
    for(int j=0;j<n;j++)
    a.m[i][j]=0;
    for(int i=0;i<n;i++)
    a.m[i][i]=1;
    for(int i=n;i<2*n;i++)
    for(int j=0;j<n;j++)
    a.m[i][j]=0;
    for(int i=0;i<n;i++)
    for(int j=n;j<2*n;j++)
    cin>>a.m[i][j],a.m[i+n][j]=a.m[i][j];
    qpow(a,k);
    for(int i=0;i<n;i++)
    {
        for(int j=n;j<2*n;j++)
        {
            cout<<ans.m[i][j]%m<<' ';
        }
        cout<<endl;
    }
    return 0;
}