基环树

在树形结构中添加1条边形成的图
分类：

• 1.无向图基环树
• 2.内向基环树，每个点出度为1的情况

一棵内向基环树

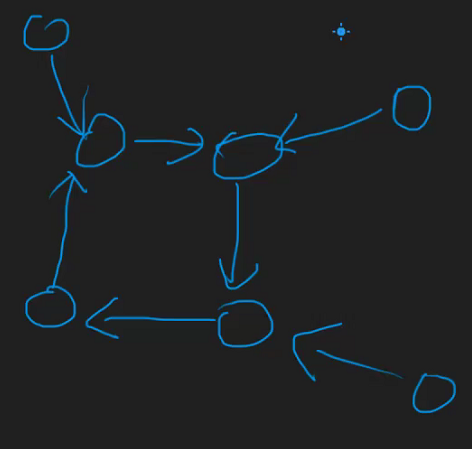
• 3.外向基环树，每个点入度为1的情况

找环

方法1：无向基环树找环

• 1.统计节点的度数deg[i]
• 2.将度数为1的点入队
• 3.循环从队首取出节点x并将x的邻接点y度数减1
• 4.若deg[y]==1,y入队，重复步骤2-4
• 5.最后deg[i]>1的点一定是环上的点

---

方法2：有向图和无向图均适用
原理：在搜索树中检查一个点x的子节点y是否深度更浅

void dfs(int cur){
	dep[cur]=dep[fa[cur]]+1;
	for(int nxt:nbr[cur]){
		if(nxt==fa[cur]) continue;
		if(dep[nxt]==0){
			fa[nxt]=cur;
			dfs(nxt);
		}
		else if(dep[nxt]<dep[cur]){
			int tmp=cur;
			while(tmp!=fa[nxt]){
				mark[tmp]=true;
				loop[++id]=tmp;
				tmp=fa[tmp];
			}
		}
	}
	return;
}

---

方法3：tarjan的拓展
原理：从环上某点x沿着某个方向到达y,当x沿另一侧再次到达点y时，dfn[y]>dfn[x]

void dfs(int cur){
	dfn[x]=++tim;
	for(int nxt:nbr[cur]){
		if(nxt==fa[cur]){
			fa[nxt]=cur;
			dfs(cur);
		}
		else if(dfn[nxt]>dfn[cur]){
			int tmp=nxt;
			while(tmp!=fa[cur]){
				mark[tmp]=true;
				loop[++id]=tmp;
				tmp=fa[tmp];
			}
		}
	}
	return;
}

使用技巧

• 1.把环当作根节点，分成环上的点和环上点的子树分别处理
• 2.把环斩断，变成1棵树处理