卡特兰数

为区别于组合数，用\(Cat(n)\)代表卡特兰数的第n项

---

是一种数列，其通项公式的一种形式为：
\(Cat_n=\frac{1}{n+1}\times C_{2n}^{n}(n=0,1,2...)\)
前几项数值为\(1,1,2,5,14,42,132,429\)
增长幅度为\(O(4^n)\)

递归定义式1

\(Cat_n=\sum_{i=0}^{n-1}Cat_i\times Cat_{n-i-1}\)
理解：对于n个点构成的二叉树，其形态有\(Cat(n)\)种
考虑dp，发现对于一个二叉树来说，枚举其左儿子大小为i,则去除根后右儿子大小为n-i+1

递归定义式2

\(Cat_n=Cat_{n-1}\times \frac{4n-2}{n+1}\)
不难发现\(\frac{4n-2}{n+1}\)的大小当n趋于正无穷大时为4,所以其增长幅度为\(O(4^n)\)

使用场景

递归定义式1适用于n不大的情况下求卡特兰数，不用处理除法(一般n<=500)

组合定义式

\(Cat_n=C_{2n}^{n}-C_{2n}^{n-1}=\frac{1}{n+1}\times C_{2n}^{n}\)
证明：

\[C_{(2n)}^{n}-C_{(2n)}^{n-1}=\frac{(2n)}{n!n!}-\frac{(2n)}{(n-1)!(n+1)!}=\frac{(2n)(n+1)}{n!n!(n+1)}-\frac{(2n)!n}{n!n!(n+1)}=\frac{(2n)!}{n!n!(n+1)}=\frac{1}{n+1}\times C_{(2n)}^{n} \]

例子

例1：01排列问题
给定n个0和n个1共2n个元素的数列，要求该数列的任意前缀，0的个数不少于1的个数，求方案数

考虑建一个坐标轴出来，选0向上走，选1向下走，那么任意时刻不能走到坐标轴以下。

先不考虑只在正半轴的条件，方案数就是$C_{2 * n}^{n} $,这时我们只需要把不符合要求的删掉。
先看下面的图，这种方案显然不合要求：

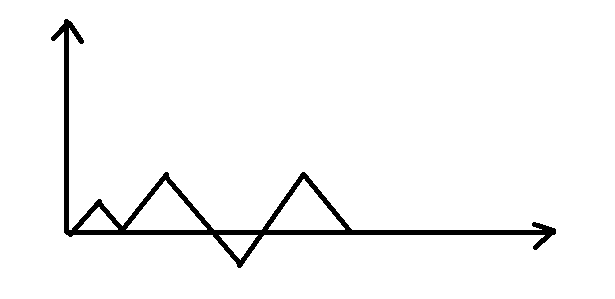
考虑这种不合法的方案,一定经过y=-1。

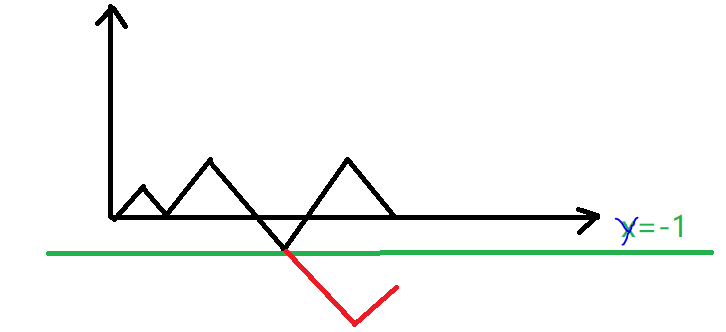
考虑对于y=-1对称，显然对称后的轨迹最后一定停留在(2* n,-2)，也就是每一条不合要求的线都可以转化为一条从原点出发，最后到x=-2的轨迹。不难看出，反过来转化也是成立的。即这两者是一一对应的。现在只要算出有多少种情况最后停留在直线x=-2上，这很简单，2* n次选择n-1次向下（或者可以说是n-1次向上）。

当然解决这个问题的模型很多（比如说这个）：

就不一一列举了。

当然还有很多例子：
例2：给定n个左括号和n个右括号，其合法的匹配序列的方案数
例3：给定n个元素，从1到n,其进出栈的不同方案数
例4：给定n条边的凸多边形，用n-3条边划分成n-2个三角形，其方案数
......
上面的几个例子都是卡特兰数