20240218笔记（数据结构）

LOJ6515. 「雅礼集训 2018 Day10」贪玩蓝月

考虑如果前端不操作，是很好做的。用一条分界线分成两半处理，只需要处理一个前缀和后缀就行了。
但是你考虑一个问题，就是可能前缀或后缀删空，这个时候直接暴力重构。假设前缀为空，就把后缀劈成两半，硬搞一个前缀出来重构，不难发现总势能是O(n)的

P3295 [SCOI2016] 萌萌哒

考虑并查集。首先可以认为有n个并查集，题目中的每一组区间关系其实对应着一些并查集的合并，最后的答案就是本质不同子序列个数

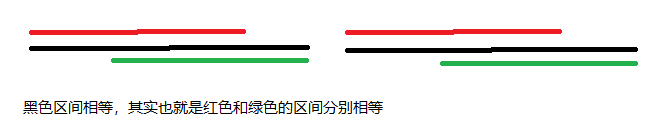
我们如何选取红色和绿色的区间呢？使用ST表。让红区间长度=绿区间长度=\(2^k\),其中\(2^k<黑区间长度<=2^{k+1}\)，这样红，绿区间覆盖了黑区间，分别相等和黑区间相等是等价的。继续分别对红，绿区间这样操作就行了。

CF1192B Dynamic Diameter

你考虑两个点x,y的深度，记他们的lca为u,有：

\[dis[x][y]=dep[x]+dep[y]-2dep[u] \]

维护出该树的全dfs序，显然u应出现在x,y中间，并且u的深度应该是最小的，那么x,y的贡献就是两者深度之和减去区间内深度最小的点。那么全dfs序上一个区间的最大贡献就是两个最大的深度减去两倍最小的深度

P6373 「StOI-1」IOI计数

比较弱智的一道题，直接线段树。考虑两个区间合并的贡献，有两种可能：
第一种是左区间的"I"拼接右区间的"OI",第二种是左区间的"IO"拼接右区间的"I"
所以合并区间的总个数=左区间"IOI"个数+右区间"IOI"个数+左区间"I"个数* 右区间"OI"个数+左区间"IO"个数+右区间"I"个数

P3987 我永远喜欢珂朵莉~

ynoi的题，难得不毒瘤（相对的），也不是分块。
考虑第一类操作，显然一个数ai的势能是它的质因子个数。那么把它分解。
假设有一个质因数为x,我们对所有满足x|ai的位置i开一棵平衡树，操作x时查询这一棵平衡树上[l,r]区间内的数，直接把这些位置暴力修改，对于第二类操作，对原序列开线段树或树状数组即可。

P4891 序列

可以分块，把序列分成sqrt(n)块。对于询问，直接暴力循环每一个块的答案
对于修改b的操作，直接暴力重构整个块。
对于修改c的操作，分情况讨论：

\[case1:\leq c \]

我们发现一件事是这种情况下不管标记是什么这个元素的值一直是b不动，所以对于这种元素我们没必要管他

\[case2:c \leq newc \leq b \]

我们发现这种情况下这个元素的值是等于newc的

\[case3:c \leq b \leq newc \]

我们发现这种情况下这个元素的值会被卡死在b上，我们知道以后newc只会越变越大，所以从此以后这个元素的值保持在b不变

\[case4:newc \leq c \leq b \]

这种情况下这个元素的值维持在c不变

所以我们只需要关注\(case2\)的元素个数了

P4340 [SHOI2016] 随机序列

考虑一段乘法段后如果有一个加号，那么这个位置也可以放减号，两者之和抵消，所以答案只与前缀乘法段的计算结果和以它为前缀的数量有关。

记\(S_i=\prod_{j=1}^{i}a_j\)
对于\(S_i\)的贡献来说，它的下一个间隙一定填加或减，如果填乘前缀的长度就会+1，所以后一个空隙有两种选择，再后面随便填，于是\(S_i\)的贡献等于：

\[S_i\times 2 \times 3^{n-i-1} \]

总答案为\(\sum_{i=1}^{n-1}S_i\times 2 \times 3^{n-i-1}+S_n\)

P3103 [USACO14FEB] Airplane Boarding G

考虑画出一只奶牛的路线图（黑色是之前的奶牛）

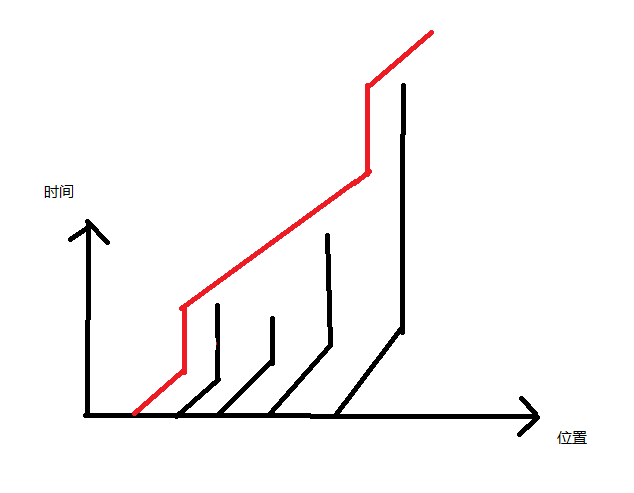
你发现奶牛的前进路线是许多段斜率为1的线段和一些竖直线段组成的，而竖直线段其实就是被前面的奶牛挡住了。
具体是怎么挡的呢，奶牛（红线）必须等到和黑线的最高点一样高才能往前走，可以理解为把黑线向左平移就可以与红线重合，那么我们就可以设计出dp,并用平衡树维护这个函数图像