全家桶

1. 1.逻辑

命题：能够判断正确或错误的叙述。

复合命题：若\(p\),则\(q\)

设原命题为若\(p\),则\(q\)，则：

• 1.逆命题：若\(q\),则\(p\)
• 2.否命题：若\(\neg p\),则\(\neg q\)
• 3.逆否命题：若\(\neg q\),则\(\neg p\)

其中原命题与逆否命题等价，逆命题与否命题等价。

条件：

若 \(p \Rightarrow q\) ,则 \(p\) 是 \(q\) 的充分条件，\(q\) 是 \(p\) 的必要条件。

p是q的充分不必要条件	\(p \Rightarrow q\)且\(q \nRightarrow p\)
p是q的必要不充分条件	\(p \nRightarrow q\)且\(q \Rightarrow p\)
p是q的充要条件	\(p \Rightarrow q\)且\(q \Rightarrow p\)
p是q的既不充分也不必要条件	\(p \nRightarrow q\)且\(q \nRightarrow p\)

量词：

• 1.全称量词：任意，符号为$\forall $
• 2.存在量词：存在，符号为$\exists $

eg1.\(\forall x \in R,有 f(x) > k\)

很典型的题目，可以转化为\(max(f(x))>k\)

eg2.\(\exists x \in R,有 f(x) > k\)

存在一个\(x\)满足条件即可，转化为\(min(f(x))>k\)

2.集合，元素

• 1.集合元素的三个特征：无序性，互异性，确定性
• 2.元素与集合之间的关系是属于或不属于，用\(\in\)或$\notin $表示
• 3.常见的集合记法：

集合	自然数集	正整数集	整数集	有理数	实数集
符号	\(N\)	\(N^{* }\)或\(N_{+}\)	\(Z\)	\(Q\)	\(R\)

ps:在符号上加$ * ,+$的上下标通常表示正的部分

集合与元素间的基本关系

若\(a\)属于集合\(A\)，记作\(a \in A\),若\(a\)不属于集合\(A\)，记作\(a \notin A\)

集合与集合间的基本关系

子集：

集合\(A\)包含于集合\(B\)(集合\(A\)是集合\(B\)的子集)，记作\(A\subseteq B\),也可以记作\(B \supseteq A\)
下面我们用数学语言解释\(A\subseteq B\)：
\(\forall x \in A\),均有\(x \in B\)。
从这条解释可以看出\(A\subseteq B\)可以得出\(x \in A\)是\(x \in B\)的充分条件，\(x \in B\)是\(x \in A\)的必要条件
\(Venn\)图:

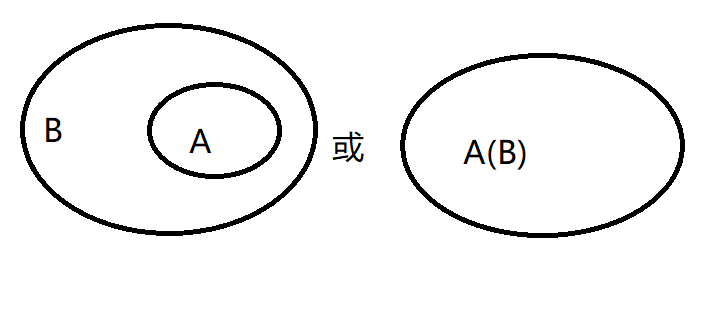
真子集：

集合\(A\)是集合\(B\)的子集，且集合\(B\)中至少有一个元素不在集合\(A\)中
\(Venn\)图:

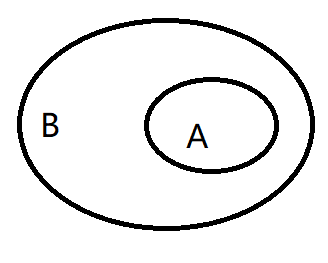
集合相等：

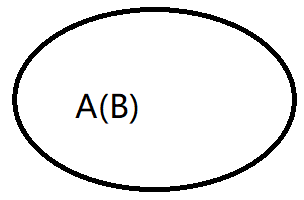
如果有\(A\subseteq B\)，\(B\subseteq A\)，称\(A=B\)
\(Venn\)图:

集合与集合间的基本运算

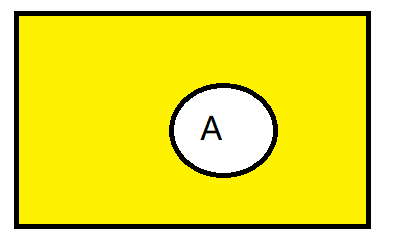
集合的并集：

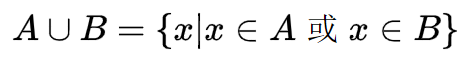
图像（黄色部分）：

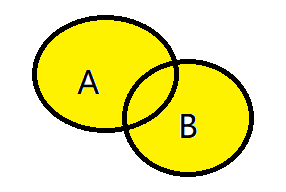
n个集合\(A_1,A_2....A_n\)的并集可以记作\(\bigcup_{i=1}^{n} A_i\)

集合的交集：

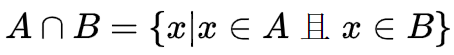
图像：

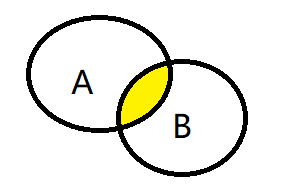
n个集合\(A_1,A_2....A_n\)的交集可以记作\(\bigcap_{i=1}^{n} A_i\)

集合的补集：

要谈补集，我们首先要钦定一个全集\(U\),\(U\)里包含了所有讨论的元素。

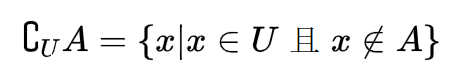
图像：

集合相乘：

就是笛卡尔积,没什么好说的。

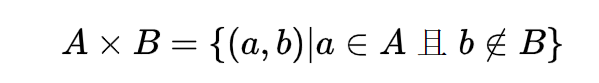
幂函数：

\(2^{A}\)={\(A\)的所有子集}

集合的运算律：

• 1.\(A \cup (B \cap C)=(A\cup B)\cap (A \cup C)\)

证明：

\(\forall x \in A \cup (B \cap C)\)

<1>若\(x \in A\),则\(x \in (A\cup B),x \in (A \cup C)\)

\(\therefore x \in (A\cup B)\cap (A \cup C)\)

<2>若\(x \in (B \cap C)\),则\(x \in B,x \in C\)

\(\therefore x \in (A \cup B),x \in (A \cup C)\)

\(\therefore x \in (A\cup B)\cap (A \cup C)\)

综上，\(A \cup (B \cap C)\subseteq (A\cup B)\cap (A \cup C)\)

\(\forall x \in (A\cup B)\cap (A \cup C)\)

\(\therefore x \in A\)

\(\therefore x \in A \cup (B \cap C)\)

\(\therefore (A\cup B)\cap (A \cup C) \subseteq A \cup (B \cap C)\)

\(\therefore (A\cup B)\cap (A \cup C) = A \cup (B \cap C)\)

---

• 2.\(A \cap (B \cup C)=(A \cap B) \cup (A \cap C)\)

证明：

\(\forall x \in A \cap (B \cup C)\)

\(\therefore x \in A,x \in (B \cup C)\)

\(\therefore x \in A,x \in B,x \in C\)

\(\therefore x \in (A \cap B) \cup (A \cap C)\)

\(\therefore A \cap (B \cup C)\subseteq (A \cap B) \cup (A \cap C)\)

\(\forall x \in (A \cap B) \cup (A \cap C)\)

<1>\(x \in (A \cap B)\)

\(\therefore x \in A,x \in B\)

\(\therefore x \in (B \cup C)\)

\(\therefore x \in A \cap (B \cup C)\)

<2>\(x \in (A \cap C)\)

\(\therefore x \in A,x \in C\)

\(\therefore x \in (B \cup C)\)

\(\therefore x \in A \cap (B \cup C)\)

综上，$ (A \cap B) \cup (A \cap C)\subseteq A \cap (B \cup C)$

\(\therefore (A \cap B) \cup (A \cap C)= A \cap (B \cup C)\)

映射

有\(A,B\)两个非空集合，若果按照某种确定的对应关系\(f\),使得对于集合\(A\)中任意的一个元素\(x\),在集合\(B\)中都有唯一确定的元素\(f(x)\)与之对应，称为\(f:A\to B\)

在\(f:A \to B\)中，\(x\)的取值范围\(A\)为映射的定义域，\(f(x)\)为\(x\)在映射\(f\)下的象集合\(f(x)=\){\(f(x)|x \in A\)}

单射：

若对于\(\forall x_1 \in A,x_2 \in A\),均满足\(f(x_1)\ne f(x_2)\),称映射\(f\)为单射。

满射：

若\(f(A)=B\),则称映射\(f\)为满射。

一一对应：

若映射\(f\)，既是单射也是满射，称映射\(f\)为一一映射，存在\(f^{-1}:B \to A\)(反函数)，使得:

• 1.\(\forall x \in A\),均有\(f^{-1}(f(x))=x\)
• 2.\(\forall y \in B\),均有\(f(f^{-1}(y))=y\)

构造映射：

\(eg1.\)构造一个一一映射\(f:\)整数集\(\to\)偶数集

\(\forall x \in Z,f(x)=2 \times x\)

\(eg2.\)构造一个一一映射\(f:\)正整数集\(\to\)整数集

\(f(1)=0,f(2)=1,f(3)=-1......\)

\(eg3.\)构造一个一一映射\(f:\)正整数集\(\to\)有理数集

这个对应有点难度，先自己想一想。
先把\(0\)单独考虑，现在每一个有理数可以对应一个最简分数$\frac{p}{q} \(,我们把每个有理数对应一个二元组\)(p,q)$,放到直角坐标系中，形成下图（先只考虑大于\(0\)的有理数）：

我们从\((1,1)\)开始，蛇行向上对应，如果不是最简分数就跳过：

怎么对应负有理数呢，一正一负就行了。

\(eg4.\)是否能构造一个一一映射\(f:\)正整数集\(\to\)实数集

先自己试着构造试试。
不难发现根本不可行，下面是证明：
反证法：
若{\(a_1,a_2,......,a_n,......\)}\(=R\)
取一个实数\(x\)使得:

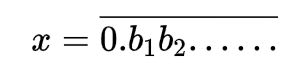
其中\(b_i \ne a_i\)的第\(i\)位小数。显然\(x\ne a_1,x\ne a_2,.....\)但\(x \in R\),与条件矛盾。

应用：

• 1.\(C_n^{k}=\frac{n!}{k!(n-k)!}\)
  首先有\(A_n^{k}=\frac{n!}{(n-k)!}\)
  试图构造一个从\(A_n^k\)到\(C_n^k\)的映射，发现有很多个排列对应一个组合。
  排列的长度是\(k\),那么自然有\(k!\)个排列对应一个组合，所以组合数的公式是\(\frac{A_n^k}{A_k^k} =\frac{n!}{k!(n-k)!}\)
• 2.\(C_n^{k}=C_n^{n-k}\)
  很好理解。当然你可以列出这两个的公式也可以构造一一对应（对应补集）
• 3.\(C_n^0+C_n^1+....+C_n^n=2^n\)
  你考虑这其实就是子集个数。

实际应用：

\(eg1.1000\)瓶药水中有一瓶有毒，每次可以取出若干瓶药水混合在一起检验是否有毒。问找到有毒的药水至少需要多少次操作。

这个问题的答案其实不难，10次，但是包含了一些思想。

---

二分法：最简单的方案，有一个问题，每次操作依赖于前一次操作的结果，若果等待前一次结果的时间很长，这就不是理想的方案。

---

二进制法：给每一瓶药水二进制编号，不会超过\(10\)位，第\(i\)次操作取二进制从前往后第\(i\)位为\(1\)的药水一起检验，\(10\)次的结果有毒记为\(1\),无毒记为\(0\)，把这十个数字放在一起形成一个二进制数，对应会编号即可。正确性是显然的

---

更深入一点思考为什么至少要进行\(10\)次操作，我们其实是在建立每一组操作结果与有毒药水编号之间的一一对应，假设进行\(9\)次操作，只有\(512\)个操作结果，无法一一对应\(1000\)个药水编号

计数

容斥原理

忘记介绍一种符号了，\(\left | A \right |\) 代表\(A\)集合中的元素个数。
容斥原理的内容：$\left | \bigcup_{i=1}^{n}A_i \right | =\sum_{i=1}^{n}\left | A_i \right | -\sum_{1<=i<j<=n}\left | A_i\cap A_j \right |+......+(-1)^{n-1}\left | A_1\cap A_2\cap ......\cap A_n \right | $

证明：
\(\forall x \in \bigcup_{i=1}^{n}A_i\)在等式左边计算一次
设\(x \in A_{i1},x \in A_{i2},......,x \in A_{ik}\),令\(S\)为\(x\)在右式的计算次数，则：
\(S=C_{k}^{1}-C_{k}^{2}+......+(-1)^{k}C_{k}^{k}\)
根据二项式定理:\((1+y)^{k}=C_{k}^{0}+C_{k}^{1} \times y+......+C_{k}^{k} \times y^{k}\)
令\(y=-1\),得：\(0=1-S,S=1\)
\(\therefore x\)在等式右边被计算一次，等式成立。

错排

通项：

根据容斥，错排的个数是全排列减去一个位置对的加上两个位置对的......
即：\(n!-C_{n}^{1} \times (n-1)!+C_{n}^{2} \times (n-2)!+......+(-1)^{n-1}C_{n}^{n}\)
\(=\sum_{i=0}^{n}(-1)! \times C_{n}^{i} \times (n-i)!\)
\(=\sum_{i=0}^{n}(-1)! \times \frac{n!}{i!(n-i)!} \times (n-i)!\)
\(=\sum_{i=0}^{n}(-1)! \times \frac{n!}{i!}\)
\(=n! \times \sum_{i=0}^{n}(-1)! \times \frac{1}{i!}\)
由\(e^{x}=1+\frac{x}{2!}+\frac{x^{2}}{3!}......\),此时令\(x=-1\)
\(\therefore e^{x}=1-\frac{1}{2!}+\frac{1}{3!}......\)，和错排的公式谜之相似，只不过是无限项，误差小于\(\frac{1}{n+1}\)
记录\(n\)个数的错排数为\(D_n,D_n\approx \frac{n!}{e}\)

递推：

\(D_n=(n-1)(D_{n-2}+D_{n-1})\)
我们假设\(1\)对应\(2\)(其他也是一样的，\(\times n-1\)就好了)，那么面临两种情况：

• 1.2对应1
  此时后面的数形成一个\(n-2\)的错排
• 2.2不对应1
  这时后面总有一个数\(k\)对应\(1\),令\(k\)对应\(2\)，对结果没有影响，这时形成一个\(n-1\)的错排

数字和固定的五位数

原问题：

数字和为6的五位数共有多少个？

很经典的插板法，记这个五位数为\(abcde\)
由题：\(a+b+c+d+e=6\),此时\(b,c,d,e\)可以为\(0\)，每一个加上\(1\),新的数是\(a(b+1)(c+1)(d+1)(e+1)\)。
\(a+(b+1)+(c+1)+(d+1)+(e+1)=10\)，插板法就可以（不可能分出来一个10以上的数），答案是\(C_9^4\)
趁机推销自己的插板法博客:组合数学初步

change 1:

数字和为40的五位数共有多少个？
\(把\overline{abcde}对应成\overline{(10-a)(10-b)(10-c)(10-d)(10-e)}\)，然后老操作，还是\(C_9^4\)

差分：

定义\(\bigtriangleup h_n=h_{n+1}-h_n\)
不难看出若\(\forall x \in n ,\bigtriangleup ^2h_x=0\)（先差分一次，再在差分数组上差分一次），{\(h_n\)}为等差数列。
同样的，若\(\forall x \in n ,\bigtriangleup ^3h_x=0\)，{\(h_n\)}为平方数数列。
更进一步的，我们发现每进行一次差分，原式的次数减一。
差分的优美性质还在于是线性算子：
\(\bigtriangleup (a_n+b_n)=\bigtriangleup a_n+\bigtriangleup b_n\)

部分均值不等式证明:

证明内容：\(\frac{\sum_{i=1}^{n}a_i}{n}>=\sqrt[n]{\prod_{i=1}^{n}a_i}\)
首先介绍一下证明方法：向前向后的数学归纳法

第一步找到一个 单调递增的发散 序列{\(a_n\)}（本文为\(2^{1},2^{2}......\)）
第二步证明若\(n=m\)时正确，则\(n=m-1\)时正确

这个做法的正确性时显然的，每一个\(n\)都可以从它后面的\(a_k\)推过来
下面是证明：

当\(n=2\)时，显然成立（自己去平方）
若\(n=2^{k}\)成立，则：
\(\frac{\sum_{i=1}^{2^{k}}}{2^{k}}=\sqrt[2^{k}]{\prod_{i=1}^{2^{k}} a_i}\)
\(\therefore n=2^{k+1}\)时，\(\frac{\sum_{i=1}^{2^{k+1}}a_i}{2^{k+1}}=\frac{\sum_{i=1}^{2^{k}}a_i}{2^{k+1}}+\frac{\sum_{i=2^{k}+1}^{2^{k+1}}a_i}{2^{k+1}}>=\frac{\sqrt[2^{k}]{\prod_{i=1}^{2^{k}} a_i}}{2}+\frac{\sqrt[2^{k}]{\prod_{i=2^{k}+1}^{2^{k+1}} a_i}}{2}\)
\(>=\sqrt[2]{\sqrt[2^{k}]{\prod_{i=1}^{2^{k}}a_i } \sqrt[2^{k}]{\prod_{i=2^{k}+1}^{2^{k+1}}a_i } }\)
\(=\sqrt[2^{k+1}]{\prod_{i=1}^{2^{k+1}}a_i }\)
\(\therefore n=2^{k+1}\)时成立
若\(n=m\)时成立，则：\(\frac{\sum_{i=1}^{m}a_i }{m}>=\sqrt[m]{\prod_{i=1}^{m}a_i }\)
\(\therefore n=m-1\)时，\(\frac{\sum_{i=1}^{m-1}a_i }{m-1}= \frac{\sum_{i=1}^{m-1}a_i +\frac{\sum_{i=1}^{m-1}a_i }{m-1} }{m}>=\sqrt[m]{\sum_{i=1}^{m-1}a_i+\frac{\sum_{i=1}^{m-1}a_i }{m-1} }=(\sum_{i=1}^{m-1}a_i )^{\frac{1}{m} } \times (\frac{\sum_{i=1}^{m-1}a_i }{m-1} )^{\frac{1}{m}}\)
\(\therefore (\frac{\sum_{i=1}^{m-1}a_i }{m-1})^{1}>=(\sum_{i=1}^{m-1}a_i )^{\frac{1}{m} } \times (\frac{\sum_{i=1}^{m-1}a_i }{m-1} )^{\frac{1}{m}}\)
\(\therefore (\frac{\sum_{i=1}^{m-1}a_i }{m-1})^{\frac{m-1}{m}}>=(\sum_{i=1}^{m-1}a_i )^{\frac{1}{m} }\)
\(\therefore \frac{\sum_{i=1}^{m-1}a_i }{m-1}>=(\sum_{i=1}^{m-1}a_i )^{\frac{1}{m-1} }\)
即\(\therefore \frac{\sum_{i=1}^{m-1}a_i }{m-1}>=\sqrt[m-1]{(\sum_{i=1}^{m-1}a_i )}\),得证

归纳与递推:

等差，等比数列基础：

等差：

\(a_n\)为第\(n\)项，\(d\)为公差，\(S_n=\sum_{i=1}^{n}a_i\)
通项：\(a_n=a_1+(n-1) \times d=dn+a_1-d\)
前缀和：\(S_n=\frac{(a_1+a_n) \times n}{2}=na_1+\frac{n \times (n-1)}{2}d\)

等比：

\(a_n\)为第\(n\)项，\(q\)为公比，\(S_n=\sum_{i=1}^{n}a_i\)
通项：\(a_n=a_1q^{n-1}(q\ne 0)\)
前缀和：

• \(1.q=1\)
  \(S_n=na_1\)
• \(2.q\ne 1\)
  采用错位相减法
  \(S_n=a_1(1+q^{1}+q^{2}+......+q^{n-1})\)
  \(qS_n=q^{1}+q^{2}+......+q^{n}\)
  \((q-1)S_n=a_1(q^{n}-1)\)
  \(S_n=\frac{a_1(1-q^{n})}{1-q}\)

西格玛（求和）：

• 1.重命名性质：求和与下标字母无关（废话）
• 2.累加性质：\(\sum_{i=1}^{n}a_i=\sum_{i=1}^{m}a_i+\sum_{i=m+1}^{n}a_i\)
• 3.线性性质：\(\sum_{i=1}^{n}ka_i=k\sum_{i=1}^{n}a_i(k为常数)\)，\(\sum_{i=1}^{n}(a_i+b_i)=\sum_{i=1}^{n}a_i+\sum_{i=1}^{n}\)
• 4.交换顺序性质：\(\sum_{j=1}^{n}(\sum_{i=1}^{m}a_{ij})=\sum_{i=1}^{m}(\sum_{j=1}^{n}a_{ij})\)
  有些人可能会觉得交换顺序没什么用，但是它很有用，看下面的例题：

eg1:求\(1\)到\(n\)的因数个数之和：

我们令\(a_{ij}=1\)表示j是i的因数，反之\(a_{ij}=0\)表示j不是i的因数，我们要求：
\(\sum_{i=1}^{n}(\sum_{j=1}^{i}a_{ij})\)
这个问题很难处理，但根据交换顺序性质：
\(\sum_{i=1}^{n}(\sum_{j=1}^{i}a_{ij})=\sum_{j=1}^{i}(\sum_{i=1}^{n}a_{ij})\)
考虑\(=\sum_{j=1}^{i}(\sum_{i=1}^{n}a_{ij})\)其实就是\(\sum_{i=1}^{n}i在1到n中的倍数个数\)

称重问题：

原问题：

一个天平，左边放被称量的物体，右边放砝码。n个不同的砝码最多可以称出多少种重量？
我们只考虑加砝码，每加一个砝码，能称量的重量分为3类：

• 1.原来能称的重量
• 2.原来能称的重量+新的砝码重量
• 3.新的砝码重量

怎么能使种数最多？三类之间没有交集，很容易可以得到递推公式\(a_n=2 \times a_{n-1}+1\)
优化这个式子，不难得出\(a_n=2^{n}-1\)
考虑怎么能使砝码的重量最小。显然\(f_1=1\)，要满足三者交集为空必定满足\(f_n>f_1+f_2+......+f_{n-1}\)，解出\(f(i)=2^{i-1}\)

change 1:

7个砝码，恰好可以称出1~100，问重量最大的砝码的重量范围？
不妨令\(f_1<=f_2<=f_3<=f_4<=f_5<=f_6<=f_7\),我们要求的就是\(f_7\)的范围
你考虑这样一件事，就是说：如果\(f_1\ne 1\),显然称不出\(1\),所以\(f_1=1\),此时\(f(2)_{ \max } =2\)(不然你称不出2),同理：
\(f(3)_{ \max } =4,f(4)_{ \max } =8,f(5)_{ \max } =16,f(6)_{ \max } =32\),此时\(f(7)_{\min}=37\)
考虑\(f(7)_{\max}\),如果\(f(7)>f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+1\)，称不出\(f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+1\),可列出关于\(f(7)\)的方程组\(f(7)<=100-f(7)+1\)，解得\(f(7)<=50\)
综上，\(37<=f(7)<=50\)

change 2:

现在右边也可以放砝码，n个不同砝码最多能称多少种重量？
每加一个砝码，能称量的重量分为4类：

• 1.原来能称的重量
• 2.原来能称的重量+新的砝码重量
• 3.原来能称的重量+新的砝码重量
• 4.新的砝码重量
  所以理论上来说，应该是\(3^n-1\)，但是你考虑放左放右都一样，所以要除以2

万恶的裂项：

裂项的精髓是抵消

eg1:

\(\sum_{i=1}^{n}\frac{1}{i(i+1)}\)
\(=\sum_{i=1}^{n}(\frac{1}{i}-\frac{1}{i+1})\)
\(=1-\frac{1}{n+1}\)

eg2:

\(\sum_{i=1}^{n}\frac{1}{i(i+1)(i+2)}\)
\(=\sum_{i=1}^{n}\frac{(i+2)-i}{i(i+1)(i+2)} \times \frac{1}{2}\)
\(=\frac{1}{2}\sum_{i=1}^{n}\left [ \frac{1}{i(i+1)}-\frac{1}{(i+1)(i+2)} \right ]\)
\(=\frac{1}{2} \times \left [ \sum_{i=1}^{n}\frac{1}{i(i+1)}-\sum_{j=2}^{n+1}\frac{1}{j(j+1)}\right ]\)
\(=\frac{1}{2}\times[\frac{1}{2}-\frac{1}{(n+1)(n+2)}]\)

eg3:

\(\sum_{i=1}^{n}i(i+1)\)
\(=\frac{1}{3}\sum_{i=1}^{n}[i(i+1)(i+2)-(i-1)i(i+1)]\)
\(=\frac{1}{3}[n(n+1)(n+2)-0]\)
\(=\frac{1}{3}n(n+1)(n+2)\)

eg4:

\(\sum_{i=1}^{n}i^3\)
\(=\sum_{i=1}^{n}\left [ i(i+1)(i+2)-3i^2-2i \right ]\)
\(=\sum_{i=1}^{n}i(i+1)(i+2)(i+3)-(i-1)i(i+1)(i+2)\)
\(=\frac{1}{4}n(n+1)(n+2)(n+3)-\frac{1}{2}n(n+1)(2n+1)-n(n+1)\)
\(=\frac{1}{4}n(n+1)[n^2+5n+6-4n-2-4]\)
\(=\frac{1}{4}n^2(n+1)^2\)

eg5:

\(\sum_{i=1}^{n}i^2\)
\(=\sum_{i=1}^{n} [i(i+1)-i]\)
\(=\frac{1}{3}n(n+1)(n+2)-\frac{1}{2}n(n+1)\)
\(=n(n+1)[\frac{1}{3}+\frac{2}{3}-\frac{1}{2}]\)
\(=\frac{1}{6}n(n+1)(2n+1)\)

数学归纳法：

eg1：

第一种归纳方法：先证明\(n=1\)时成立，再证明若\(n=k\)成立，\(n=k+1\)成立
求证：
\(1+3+5+......+(2n-1)=n^2\)
解：
当\(n=1\)时,左边\(=1\) ,右边\(=1²=1\)
假设当\(n=k\)时,左边\(=1+3+5+……+(2k-1)\),右边\(=k²\)
当\(n=k+1\)时,
两边加 \(2(k+1)-1=2k+1\)
得左边\(=1+3+5+……+(2k-1)+2(k+1)-1= k²+2k+1=(k+1)²\)
得证

eg2:

第二种归纳方法：先证明\(n=1\)时成立，再证明若\(n=\forall 1<= i <=k\)时成立，\(n=k\)时成立
求证：
正实数数列{\(x_m\)}满足\(x_1^3+x_2^3+......+x_n^3=(x_1+x_2+......+x_n)^2\)
解：
当\(x=1\)时，左边\(=x_1^3\),右边\(=x_1^2\)
\(\therefore x_1^3=x_1^2\)
\(\because x_1>0\)
\(\therefore x_1=1\)
若\(\forall 1<=i<=k,x_i=i\)
则：\(1^3+2^3+....+k^3+x_{k+1}^3=(1+2+....+k+x_{k+1})^2\)
\(\therefore \frac{k^2(k+1)^2}{4}+x_{k+1}^3=\frac{k^2(k+1)^2}{4}+k(k+1)x_{k+1}+x_{k+1}^2\)
\(\therefore x_{k+1}^2-x_{k+1}-k(k+1)=0\)
\(\therefore (x_{k+1}+k)(x_{k+1}-k-1)\)
\(\because x_{k+1}>0\)
\(\therefore x_{k+1}=k+1\),得证

eg3:

第三种归纳方法，详见均值不等式的部分证明

递推公式转化通项公式：

eg1:

\(a_1=1\)
\(a_{n+1}=2 \times a_n+1\)

way 1:

解：
设\(a_{n+1}+k=2(a_n+k)\)
\(\therefore 2 \times k-1=1\)
\(\therefore k=1\)
\(\therefore a_{n+1}+1=2(a_n+1)\)
\(\because a_1+1=2\)
\(\therefore a_{n}+1=2^{n}\)
\(\therefore a_{n}=2^{n}-1\)

way2:

解：
\(\because a_{n+1}=2 \times a_{n}+1\)
\(\therefore \frac{a_{n+1}}{2^{n+1}}=\frac{a_{n}}{2^{n}}+\frac{1}{2^{n+1}}\)
令\(b_{n}=\frac{a_{n}}{2^{n}}\)
\(\therefore b_{n+1}=b_{n}+\frac{1}{2^{n+1}}\)
\(\therefore b_n=\frac{1}{2}+\frac{1}{4}+......+\frac{1}{2^{n}}=1-\frac{1}{2^{n}}\)
\(\therefore a_n=2^{n}-1\)

eg2:

\(a_1=1\)
\(a_{n+1}=2a_n+2^{n}\)
解：
\(\because a_{n+1}=2a_n+2^{n}\)
\(\therefore\frac{a_{n+1} }{2^{n+1}}= \frac{a_{n} }{2^{n}}+\frac{1}{2}\)
令\(b_n=\frac{a_n}{2^n}\)
\(\therefore b_{n+1}=b_n+\frac{1}{2}\)
\(\because b_1=\frac{1}{2}\)
\(\therefore b_n=\frac{n}{2}\)
\(\therefore a_n=n \times 2^{n-1}\)

eg3:

\(a_1=1\)
\(a_{n+1}=2a_n+n\)

way1:

解：
设\(a_{n+1}+k(n+1)+b=2(a_n+kn+b)\)
\(\therefore \forall n,n=kn-k+b\)
解得\(k=1,b=1\)
\(\therefore a_{n+1}+(n+1)+1=2(a_n+n+1)\)
\(\because a_1+1+1=3\)
\(\therefore a_n+n+1=3 \times 2^{n-1}\)
\(\therefore a_n=3 \times 2^{n-1}-n-1\)

way2:

解：
\(\frac{a_{n+1} }{2^{n+1}} =\frac{a_{n} }{2^{n}}+\frac{n}{2^{n+1}}\)
\(\frac{a_{n} }{2^{n}} =\frac{1}{2}+\sum_{i=1}^{n-1}\frac{i}{2^{i+1}}\)
\(\sum_{i=1}^{n-1}\frac{i}{2^{i+1}}=\)
\(\sum_{i=1}^{n-1}\frac{i}{2^{i+1}}=\sum_{i=1}^{n-1}\frac{1}{2^{i+1}} \times i\)
设\(S_i=\frac{1}{2^{i+1}}\),则\(S_n=\frac{1}{2}-\frac{1}{2^{n+1}}\)
\(\therefore \sum_{i=1}^{n-1}\frac{i}{2^{i+1}}=\sum_{i=1}^{n-1}(S_i-S_{i-1})=S_{n-1}(n-1)-\sum_{i=1}^{n-2} S_i\)
\(=(\frac{1}{2}-\frac{1}{2^n})(n-1)-\sum_{i=1}^{n-2}(\frac{1}{2}-\frac{1}{2^{i+1}})\)
\(=(\frac{1}{2}-\frac{1}{2^n})(n-1)-\frac{n-2}{2}+(\frac{1}{2}-\frac{1}{2^{n-1}})\)
\(=1-\frac{n-1}{2^n}-\frac{1}{2^{n-1}}\)
\(=\frac{2^n-n-1}{2^n}\)
\(\therefore \frac{a_n}{2^n}=\frac{1}{2}+\frac{2^n-n-1}{2^n}\)
\(=\frac{2^n+2^{n-1}-n-1}{2^n}\)
\(\therefore a_n=2^n+2^{n-1}-n-1\)
\(=3 \times 2^{n-1}-n-1\)

数论:

在开头表明一点，数论只关心整数

定义1.1整除

\(a\)整除\(b\)记为\(a|b\)

\(a|b\)指\(\exists n\in \mathbb{Z},使得b=an\)

定义1.2

• 1.整除的传递性：\(a|b,b|c\Rightarrow a|c\)

• 2.整除的可加性：\(n|a,n|b\Rightarrow n|a\pm b\)

• 3.整除的可乘性：\(a|b,c|d\Rightarrow ac|bd(a|b\Rightarrow a|bd)\)

eg1:

证明：如果\(3|x,7|x\Rightarrow 21|x\)

解：

\(21|x,21|3x\)

\(\therefore 21|7x-3x-3x\)

即\(21|x\)

eg2:

证明\(8|3^{2n+1}+5\)

解：

\(3^{2k+1}+5=3^{2k-1}-3+8=3 \times (3^{2k}-1)+8=3(9^k-1)+8=3 \times 8 \times (9^{k-1}+....+9+1)+8\)

定义2.1最大公因数

\(gcd(a,b):max\){\(m|m|a且m|b\)}

\(lcm(a,b):min\){\(n|a|n且b|n,n>0\)}

引理2.2带余除法

ps:2.2~2.7中(a,b)默认为gcd(a,b)
\(\forall a,b>0,\exists 唯一q,r使得 \begin{Bmatrix} a=bq+r \\ 0<=r<=b-1 \end{Bmatrix}\)

设\(r>=b\)

\(\therefore a-(k+1)b>=0\)

令\(r_1=a-(k+1)b\)

\(\therefore r_1<r,矛盾\)

\(\therefore\)存在一组\(q,r\)

下面证明\(q,r\)唯一

若\(a=bq_1+r=bq_2+r_2\)

\(\therefore \left | b(q1-q2) \right | =\left | r2-r1 \right |<=max(r2,r1)<=b-1\)

\(\because \left | b(q1-q2) \right | \mid b\)

\(\therefore q1-q2=0,q1=q2\)

\(\therefore q1=q2,r1=r2\)，矛盾。

\(q,r\)唯一。

定理2.3公倍数能被最小公倍数整除：

即证明：\(a|n,b|n\Rightarrow lcm(a,b)|n\)

解：

设\(n{\div} lcm(a,b)=q...r\)

\(\therefore n=qlcm(a,b)+r\)

\(a|n-qlcm(a,b)=r\)

同理，\(b|r\)

\(\therefore r\)也是\(a,b\)的公倍数

而\(0<=r<lcm(a,b)\),矛盾

引理2.4辗转相除法

若\(a{\div}b=q...r,则(a,b)=(b,r)\)

首先考虑如果\((a,b)=(a-b,b)\)，就可以通过多次相减把\((a,b)\)变成\((r,b)\)，下文证明：\((a,b)=(a-b,b)\)

\(\forall x \in a,b的公因数，有x|a,x|b\)

\(\therefore x|a-b\)

\(\therefore x \in a-b与b的公因数\)

\(a与b的公因数\subseteq a-b与b的公因数\)

同理可得：\(a-b与b的公因数\subseteq a与b的公因数\)

\(\therefore a与b的公因数= a-b与b的公因数\)

\(\therefore (a,b)=(a-b,b)\),得证

裴蜀定理

内容：

\(\forall a,b,\exists x,y使得ax+by=(a,b)\)

证明：

不妨令\(a>b\)

\(a_1=a,b_1=b,a1{\div} b_1=q_1....r_1\)

\(令a_2=b_1,b_2=a_1,a_2{\div } b_2=q_2....r_2\)

......

\(直到r_n=0时，(a_n,b_n)=b_n\)

\(\therefore (a,b)=a_nq_n\)

感性理解一下可以倒退回第一个式子。

其实只是作者太拉，不知道怎么形容

推论2.5

• 1.公因数整除最大公因数

• 2.整除的互质可消性

证明一下第2点，即证明：若\((a,b)=1,a|bc\)则\(a|c\)

由裴蜀定理得:\(\exists x,y使得ax+by=(a,b)\)

\(\therefore acx+bcy=c\)

\(\because a|bc\)

\(\therefore a|bcy\)

又\(\because a|acx\)

\(a|acx+bcy=c\)

性质2.6

• \(1.(a,b,c)=((a,b),c)\)

• \(2.(a,b)=(a,b,ax)\)

• \(3.(a,b,c)=((a,b),(a,c))\)

例子2.7

eg1:

求证，已知a,b为正整数，\((2^{a-1},2^{b-1})=2^{(a,b)}-1\)

证明：

若\(a>b,(2^{a}-1-2^{a-b}(2^b-1),2^b-1))=(2^{a-b}-1,2^b-1)=2^{(a,b)}-1\)

eg2:

求证，已知\(a,b\)为正整数，\((2^{2^a}+1,2^{2^b}+1)=1\)

原式\(=(2^{2^a}-1+2,2^{2^b}+1)=((2^{2^{a-1} }+1 )(2^{2^{a-1} }-1)......(2^{2^{b} }+1)(2^{2^{b} }-1)+2,2^{2^{b} }+1)=(2,2^{2^{b} }+1)=1\)

定义3.1质数：

\(p>2,n|p\Rightarrow n=1或n=p\)

eg1:

证明存在无穷个质数

根据2.7eg2,\((2^{2^a}+1,2^{2^b}+1)=1\)

\(\therefore 2^{2^a}+1与2^{2^b}+1的质因子互不相同\)，得证

eg2:

证明若\(2^n-1\)为质数，\(n\)必为质数

设\(n=ab\)

根据2.7eg1,\((2^a-1,2^n-1)=2^{(a,n)}-1=2^a-1\)

\(\therefore 2^a-1|2^n-1\),矛盾，得证

定理3.2唯一分解定理

可行性：

当\(n=2\)时，可分解。

若\(n=2,3,....,k\)时均可分解，当\(n=k+1时\)

• 1.\(k+1\)时质数——自身就是分解

• 2.一定有\(k+1=ab\)，从\(a,b\)的分解推过来

唯一性：

设\(n=p_1p_2....p_s=q_1q_2....q_t(s>=t)\)

\(\because p_1|q_1q_2....\)

\(\therefore p_1|q_i,等价于p_1|q_1\)

由此可得\(p_{t+1}p_{t+2}....p_{s}=1\),矛盾，得证。

定义3.3

定义\(v_p(n):n\)的标准分解式中所含质因子\(p\)的指数

\(v_p(n1n2)=vp(n1)+vp(n2)\)

\(v_p(gcd(n1,n2))=min(v_p(n1),v_p(n2))\)

\(v_p(lcm(n1,n2))=max(v_p(n1),v_p(n2))\)

\[v_p(n1+n2)= \begin{Bmatrix} min(v_p(n1),v_p(n2))(v_p(n1)\ne v_p(n2)) \\ >=v_p(n1)=v_p(n2) \end{Bmatrix}\]

\(v_p(n!)=\sum_{i=1}^{\infty } \left \lfloor \frac{n}{p^i} \right \rfloor\)

\(v_p(C_{n}^{m})=\sum_{i=1}^{\infty } \left \lfloor \frac{n}{p^i} \right \rfloor-\left \lfloor \frac{m}{p^i} \right \rfloor-\left \lfloor \frac{n-m}{p^i} \right \rfloor\)

最下面式子的含义正好是\(n+(n-m)\)在\(p\)进制下的进位个数

推论3.4

设正整数n的标准分解式为\(:n=p1^{e_1}p2^{e_2}...pk^{e_k}\)

设\(m=p1^{f_1}p2^{f_2}...pk^{f_k}\),则\(m|n\Rightarrow f_i<=e_i(1<=i<=k)\)

因数个数公式：

\[\tau (n)=(e_1+1)(e_2+1)....(e_k+1) \]

因数和公式：

\[\sigma(n)=\frac{p_1^{e_1+1}-1}{p_1-1} \frac{p_2^{e_2+1}-1}{p_2-1}.... \frac{p_k^{e_k+1}-1}{p_k-1} \]

因数积公式：

\[n^{\frac{\tau (n)}{2} } \]

eg1:

证明\(6|n^3+5n\)
\(n^3+5n=n^3-n+6n=(n-1)n(n+1)+6n\)

eg2:

设\(a,b,c,d\)是正整数，满足\(a^5=b^4,c^3=d^2,c-a=19\)，求\(d-b\)
设\(a^5=b^4=m^20,c^3=d^2=n^6\)
\(\therefore a=m^4,b=m^5,c=n^2,d=n^3\)
\(\because c-a=19\)
\(\therefore n^2-m^4=19\)
\(\therefore (n+m^2)(n-m^2)=19\)
\(\therefore n=10,m=3\)
\(\therefore d-b=757\)

eg3:

已知\(p\)为质数，\(x,y\)为正整数，求解方程\(p^x=y^3+1\)
\(y^{3}+1=(y+1)\left(y^{2}-y+1\right)\)
\(特判其中一个是一解得 y=1, p=2, x=1\)
\(\operatorname{gcd}\left(y+1, y^{2}-y+1\right)=\operatorname{gcd}(y+1,3) (辗转相除法)\)
\(故 p=3 ，解得 x=3, y=3\)

定理3.7

设正整数\(m,n\)的标准分解式为：\(m=p_1^{f_1}p_2^{f_2}....p_k^{f_k},n=p_1^{g_1}p_2^{g_2}....p_k^{g_k}\)

• 1.最大公因数：\((m,n)=p_1^{min(f_1,g_1)}p_2^{min(f_2,g_2)}....p_k^{min(f_k,g_k)}\)
• 2.最小公倍数：\([m,n]=p_1^{max(f_1,g_1)}p_2^{max(f_2,g_2)}....p_k^{max(f_k,g_k)}\)

推论3.8

• 1.\((ma,mb)=m(a,b)\)
  显然，就不证明了
• 2.\((a,uv)=(a,(a,u)v)\)
  \(右式=(a,(av,uv))\)
  \(根据性质2.6，(a,(av,uv))=((a,av),uv)=(a,uv)=左式\)，得证
• 3.\((u,v)=1 \Rightarrow (a,uv)=(a,u)(a,v)\)
  \(u,v\)无公因数，分开结果一样
• 4.\((a,b)=1,(c,d)=1\Rightarrow (ab,cd)=(a,c)(a,d)(b,c)(b,d)\)
• 5.\((a,b)=1\Rightarrow (a^k,b^k)=1\)
  可以参考质因数分解理解

定义4.1同余

\(n|a-b\Rightarrow a\equiv b(\bmod n)\)

性质4.2同余的性质

• 1.若\(a\equiv b(\bmod n)\),则\(a\)与\(b\)对\(n\)作带余除法所得的余数相同
• 2.自反性：\(a\equiv b(\bmod n)\Rightarrow b\equiv a(\bmod n)\)
• 3.传递性：\(a\equiv b(\bmod n),b\equiv c(\bmod n)\Rightarrow a\equiv c(\bmod n)\)
• 4.可加减性：\(a_1\equiv a_2(\bmod n)，b_1\equiv b_2(\bmod n)\Rightarrow a_1\pm b_1\equiv a_2\pm b_2\)
• 5.可乘性：\(a_1\equiv a_2(\bmod n)，b_1\equiv b_2(\bmod n)\Rightarrow a_1\pm b_1\equiv a_2\pm b_2\)
• 6.可除性：\(ka\equiv kb(\bmod kn)\Rightarrow a\equiv b(\bmod n)\)，不能直接除
• 7.互质可除性：\(ka\equiv kb(\bmod n),(k,n)=1\Rightarrow a\equiv b(\bmod n)\)

例子4.3：

eg1:

已知\(n=12345678910...20212022\),求\(n除以11的余数\)
\(n \equiv 123456789+1011....99+100....999+1000....2022\equiv 5+(10+....+99)+(999-998+....+101-100)+(1001+....+2022\equiv 5+10+10 \equiv 3)\)

eg2:

求证:\(1984|993^{993}+991^{991}\)
\(993^{993}+991^{991}\equiv 993^{993}+(-993)^{991}\equiv 993^{991}(993^2-1)\equiv 993^{991}(993+1)(993-1)\equiv 993^{991} \times 497 \times 2 \times 992 \equiv 0\),得证。

定理4.4费马小定理

内容：\(若p是质数，a是任意一个数，则有a^p\equiv a(\bmod p)\)

• 1.\(a是p的倍数\)，显然
• 2.\(a不是p的倍数\)
  原命题等价于\(a^p-a是p的倍数\)
  令\(b=a-1\)
  \(\therefore a^p-a=(b+1)^p-(b+1)=b^p+C_{p}^1b^{p-1}+....+C_{p}^{p-1}b+1-b-1(二项式定理)\)
  \(\equiv b^p-b(\bmod p)\)
  \(\therefore 若b^p\equiv b(\bmod p)成立，b+1^p\equiv b+1(\bmod p)成立\)
  相信看到这里的读者都想到了数学归纳法。
  \(\because 1^p\equiv 1(\bmod p)\)
  \(\therefore a^p\equiv a(\bmod p)成立\)
  但是注意：有的合数\(p\)也满足费马小定理(卡迈尔数)，但是很少，所以费马小定理可以作为一个检验质数的标准

定义5.1

剩余类：

把\(\mathbb{z}按照\bmod n\)分为\(0(\bmod n),1(\bmod n)....n-1(\bmod n)\)
\(\mathbb{z_n}=\){\(\overline{0}, \overline{1},.... \overline{n-1}\)}
\(\overline{a}+\overline{b}=\overline{a+b}\)
\(\overline{a}-\overline{b}=\overline{a-b}\)
也可以乘，但除可能无解。

完全剩余系（完系）：

\(x=\){\(a_i \in \overline{i}|0<=i<=n-1\)}
那么显然\(y=\){\(b_i|b_i=a_i+k,k \in \mathbb{N}\)}也是一个完全剩余系
\(z=\){\(b_i|b_i=a_i\times k,k \in \mathbb{N},且gcd(k,n)\)}也是一个完全剩余系

既约剩余系：

也称简化剩余系或缩系，是m的完全剩余系中与m互素的数构成的子集，如果模m的一个剩余类里所有数都与m互素，就把它叫做与模m互素的剩余类。在与模m互素的全体剩余类中，从每一个类中各任取一个数作为代表组成的集合，叫做模m的一个简化剩余系。

欧拉函数：

\(\varphi(n)=0到n-1中与n互质的数的个数\)
积性：\(m,n互质\Rightarrow \varphi(n)\times \varphi(m)=\varphi(nm)\)
计算欧拉函数可以积性证明，也可以考虑容斥：
$令数列 p 为唯一分解后 n 的质因子数列， k 为质因子数， A_{i} 为 p_{i} 倍数个数 则 \varphi(n)=n-\left|\bigcup_{i=1}^{n} A_{i}\right|=n \prod_{i=1}^{k}\left(1-p_{i}\right) $

逆元：

若\(a\times b \equiv 1(\bmod n)\),则称\(b为a在\bmod n意义下的逆元(a^{-1}=b)\)，且\(b在\bmod n意义下唯一\)

证明：

1.裴蜀定理可以证明存在性：
\(\forall x,y\)使\(ax+yn=1\)
\(\therefore ax \equiv 1(mod n)\)
2.存在和唯一可以一起证明：
{\(0,1,...,n\)}是完系，\(\times a\)还是一个完系而且完系中\(b \in \overline{1}\)是唯一的

性质：

• 1.\(a {\div} b=a^b{-1}\)

---

而且对于任意质数\(p\)其完系\(Z_p\)是四则运算封闭的。

例题：

eg1:

证明：\(p\)为奇质数，若\(1+\frac{1}{2}+....+\frac{1}{p-1},(m,n)\)，则\(p|m\)
原式\(=(1+\frac{1}{p-1})+(\frac{1}{2}+\frac{1}{p-2})+...\),此时每个括号内通分分子为\(p\)，得证

eg2:

求\(C_{100}^{73} (\bmod 101)\)
\(C_{100}^{73}=\frac{100!}{73!27!}\equiv 100!(73!27!)\equiv 100!(73!(-1)^{27}74\times 75.....\times 100)^{-1}\equiv 100!(-(100!))^{-1}\equiv -1\)
同理可得\(C_{p-1}^{m} \equiv (-1)^m (\bmod p)\)
还有一个性质：$C_{n}^{p}=\left \lfloor \frac{n}{p} \right \rfloor $，但作者太拉不会证

定理5.2中国剩余定理：

已知\(n_1,n_2,...,n_k\)两两互质，同余方程组：

\[\begin{Bmatrix} x\equiv a_1(\bmod n_1) \\ x\equiv a_2(\bmod n_2) \\ ... \\ x\equiv a_n(\bmod n_k) \end{Bmatrix}\]

在模\(n=n_1n_2....n_k\)的意义下有唯一解。
举个例子：

\[\begin{Bmatrix} x\equiv a_1(\bmod 3) \\ x\equiv a_2(\bmod 5) \\ x\equiv a_3(\bmod 7) \end{Bmatrix}\]

对于这个问题有一个奇妙的解法。考虑如果条件是被3,5,7整除，问题就很好做。求出最小公倍数即可。显然这个数可以是105的任意倍。

如果条件是除以3余1，被5和7整除，问题也很好做，在被5,7整除的数中找一个除以3余1的，易知最小满足要求的数是70。同理除以5余1，被3和7整除的最小数是21，理除以7余1，被3和5整除的最小数是15.

除以3的余数	除以5的余数	除以7的余数	最小满足要求的数
0	0	0	105
1	0	0	70
0	1	0	21
0	0	1	15

考虑第二行，70除以3余1，被5,7整除，那么显然140也被整除，而除以3的余数变成了2，正好是70的两倍。

如果再把140加上21呢（也就是161），因为21被3和7整除，所以161除以3和7的余数和140的一样，除以5的余数则是变成了21的1。

有一个显然的结论，一个大于105的数，减去105后，除以3,5,7的余数不会发生改变。所以35和140除以3,5,7的余数一样，56和161除以3,5,7的余数也一样。

除以3的余数	除以5的余数	除以7的余数	满足要求的数
2	0	0	140
2	1	0	161

除以3的余数	除以5的余数	除以7的余数	最小满足要求的数
2	0	0	35
2	1	0	56

可以归纳出通解：
\(设 M_{i}=\frac{n_{1} n_{2} n_{3} \cdot n_{k}}{n_{i}}\)
\(解为 x \equiv \sum_{i=1}^{k} a_{i} M_{i} M_{i}^{-1} ，其中的逆元是 \bmod 对应的 n_{i} 的逆\)

定义5.3素数域

记得开头的话吗，数论只关心整数，所以怎么在整数里定义类似除法的运算?
首先\(a{\div} b\),可以理解为\(a\times b^{-1}\),关键就在找到\(b的逆元\),而这在完全剩余系里非常好理解，下面是一个\(\bmod 7\)的完全剩余系：

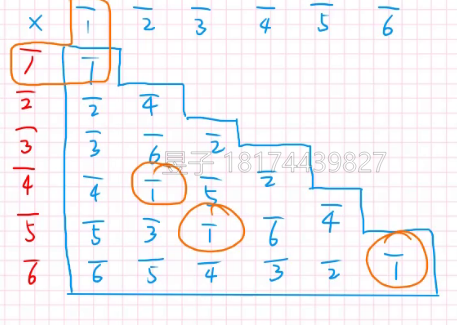
现在有逆元了，比如\(\overline{4}^{-1} = \overline{2}\)
计算一个式子帮助理解：
\(\overline{5} {\div}\overline{4}=\overline{5} \times \overline{2}=\overline{3}\)
为什么叫素数域，因为你考虑每个元素都要有逆元，只能是素数了。

定义6.1数论函数

定义域是整数的函数

定义6.2积性函数和完全积性函数

充要判定条件：
积性函数：

\[\begin{Bmatrix} f(n)=f(p_1^{e_1})....f(p_m^{e_m}) \\ f(1)=1 \end{Bmatrix}\]

完全积性函数：

\[\begin{Bmatrix} f(n)=f(p_1)^{e_1}....f(p_m)^{e_m} \\ f(1)=1 \end{Bmatrix}\]

易知：3.4的因数个数公式，因数个数公式；5.1的欧拉函数都是积性函数

群论：

对于一个非空集合 \(G\) 和某操作 \(* ，(G, *)\) 称为一个群，其中 \(*\) 是任意一个二元运算， \(G\) 有限称为有限群
性质:

• \(存在单位元 e 使得 \forall g \in G 使得 g * e=e * g=g\)
• \(\forall g \in G, \exists g^{\prime} \in G 使得 g * g^{\prime}=g^{\prime} * g=e ， g 和 g^{\prime} 互为逆元记作 g^{-1}\)
• \(\forall g_{1}, g_{2}, g_{3} ，满足 g_{1} *\left(g_{2} * g_{3}\right)=\left(g_{1} * g_{2}\right) * g_{3}\) ，也就是说群有结合律，但注意 不一定有交换律
• 群内元素运算后仍在群内
  单位元是唯一的，因为设存在两个，则这俩运算分别等于其中一个故两个相等
  如果 \(a * b=b * a\) 则称为一个交换群或阿贝尔群
  一个群的阶就是其集合的元素个数
  如果 \(\exists H \subseteq G\) 并且 \((H, *)\) 也是群则称 \(H\) 是 \(G\) 的子群
  任意群都有 \((e, *)\) 和 \((G, *)\) ，这两个称为平凡子群
  定义一个置换是一个从排列 \(1 \rightarrow n\) 向排列 \(p\) 的映射

\[\left\{\begin{array}{c} a_{1} a_{2} \ldots a_{n} \\ a_{p 1} a_{p 2} \ldots a_{p n} \end{array}\right\}\]

意思是 把 \(a_{i}\) 映射到 \(a_{p i}\)
置换支持乘法，两个置换 \(f, g\) 相乘就是先进行 \(f\) 映射再进行 \(g\) 映射
在置换群的作用下，元素存在等价关系。等价关系即满足自反性、对称性、传递性。满足等价关系的元素处于同一个等价类中
置换群的子群同样是一个置换群
循环群:指一个群 \((G, *)\) ，其中 \(G=\left\{a^{m} \mid m \in \mathbb{Z}\right\}\) 称为一个由 \(a\) 生成的循环群
若运算是乘法，循环群显然是交换群
假设群 \((G, \circ)\) 和群 \((H, \cdot)\) 之间存在双射 \(f: G \rightarrow H\) ，使得 \(f(a)=A 和 f(b)=B\) ，如果这两个群是同构的，那么 \(a \circ b 应对应 A \cdot B\) ，即 \(f(a \circ b)=A \cdot B=f(a) \cdot f(b)\) . 该条件必须对 \(\mathrm{G}\) 中所有的元素 \(\mathrm{a} 和 \mathrm{b}\) 都成立，以上是同构的含义
一个元素在群中的阶就是说最小的 \(k\) 使得 \(g^{k}=e\) ， \(k 就是元素 g 的阶记作 o(g)\)