数论

在开头表明一点，数论只关心整数

定义1.1整除

\(a\)整除\(b\)记为\(a|b\)

\(a|b\)指\(\exists n\in \mathbb{Z},使得b=an\)

定义1.2

• 1.整除的传递性：\(a|b,b|c\Rightarrow a|c\)

• 2.整除的可加性：\(n|a,n|b\Rightarrow n|a\pm b\)

• 3.整除的可乘性：\(a|b,c|d\Rightarrow ac|bd(a|b\Rightarrow a|bd)\)

eg1:

证明：如果\(3|x,7|x\Rightarrow 21|x\)

解：

\(21|x,21|3x\)

\(\therefore 21|7x-3x-3x\)

即\(21|x\)

eg2:

证明\(8|3^{2n+1}+5\)

解：

\(3^{2k+1}+5=3^{2k-1}-3+8=3 \times (3^{2k}-1)+8=3(9^k-1)+8=3 \times 8 \times (9^{k-1}+....+9+1)+8\)

定义2.1最大公因数

\(gcd(a,b):max\){\(m|m|a且m|b\)}

\(lcm(a,b):min\){\(n|a|n且b|n,n>0\)}

引理2.2带余除法

ps:2.2~2.7中(a,b)默认为gcd(a,b)
\(\forall a,b>0,\exists 唯一q,r使得 \begin{Bmatrix} a=bq+r \\ 0<=r<=b-1 \end{Bmatrix}\)

设\(r>=b\)

\(\therefore a-(k+1)b>=0\)

令\(r_1=a-(k+1)b\)

\(\therefore r_1<r,矛盾\)

\(\therefore\)存在一组\(q,r\)

下面证明\(q,r\)唯一

若\(a=bq_1+r=bq_2+r_2\)

\(\therefore \left | b(q1-q2) \right | =\left | r2-r1 \right |<=max(r2,r1)<=b-1\)

\(\because \left | b(q1-q2) \right | \mid b\)

\(\therefore q1-q2=0,q1=q2\)

\(\therefore q1=q2,r1=r2\)，矛盾。

\(q,r\)唯一。

定理2.3公倍数能被最小公倍数整除：

即证明：\(a|n,b|n\Rightarrow lcm(a,b)|n\)

解：

设\(n{\div} lcm(a,b)=q...r\)

\(\therefore n=qlcm(a,b)+r\)

\(a|n-qlcm(a,b)=r\)

同理，\(b|r\)

\(\therefore r\)也是\(a,b\)的公倍数

而\(0<=r<lcm(a,b)\),矛盾

引理2.4辗转相除法

若\(a{\div}b=q...r,则(a,b)=(b,r)\)

首先考虑如果\((a,b)=(a-b,b)\)，就可以通过多次相减把\((a,b)\)变成\((r,b)\)，下文证明：\((a,b)=(a-b,b)\)

\(\forall x \in a,b的公因数，有x|a,x|b\)

\(\therefore x|a-b\)

\(\therefore x \in a-b与b的公因数\)

\(a与b的公因数\subseteq a-b与b的公因数\)

同理可得：\(a-b与b的公因数\subseteq a与b的公因数\)

\(\therefore a与b的公因数= a-b与b的公因数\)

\(\therefore (a,b)=(a-b,b)\),得证

裴蜀定理

内容：

\(\forall a,b,\exists x,y使得ax+by=(a,b)\)

证明：

不妨令\(a>b\)

\(a_1=a,b_1=b,a1{\div} b_1=q_1....r_1\)

\(令a_2=b_1,b_2=a_1,a_2{\div } b_2=q_2....r_2\)

......

\(直到r_n=0时，(a_n,b_n)=b_n\)

\(\therefore (a,b)=a_nq_n\)

感性理解一下可以倒退回第一个式子。

其实只是作者太拉，不知道怎么形容

推论2.5

• 1.公因数整除最大公因数

• 2.整除的互质可消性

证明一下第2点，即证明：若\((a,b)=1,a|bc\)则\(a|c\)

由裴蜀定理得:\(\exists x,y使得ax+by=(a,b)\)

\(\therefore acx+bcy=c\)

\(\because a|bc\)

\(\therefore a|bcy\)

又\(\because a|acx\)

\(a|acx+bcy=c\)

性质2.6

• \(1.(a,b,c)=((a,b),c)\)

• \(2.(a,b)=(a,b,ax)\)

• \(3.(a,b,c)=((a,b),(a,c))\)

例子2.7

eg1:

求证，已知a,b为正整数，\((2^{a-1},2^{b-1})=2^{(a,b)}-1\)

证明：

若\(a>b,(2^{a}-1-2^{a-b}(2^b-1),2^b-1))=(2^{a-b}-1,2^b-1)=2^{(a,b)}-1\)

eg2:

求证，已知\(a,b\)为正整数，\((2^{2^a}+1,2^{2^b}+1)=1\)

原式\(=(2^{2^a}-1+2,2^{2^b}+1)=((2^{2^{a-1} }+1 )(2^{2^{a-1} }-1)......(2^{2^{b} }+1)(2^{2^{b} }-1)+2,2^{2^{b} }+1)=(2,2^{2^{b} }+1)=1\)

定义3.1质数：

\(p>2,n|p\Rightarrow n=1或n=p\)

eg1:

证明存在无穷个质数

根据2.7eg2,\((2^{2^a}+1,2^{2^b}+1)=1\)

\(\therefore 2^{2^a}+1与2^{2^b}+1的质因子互不相同\)，得证

eg2:

证明若\(2^n-1\)为质数，\(n\)必为质数

设\(n=ab\)

根据2.7eg1,\((2^a-1,2^n-1)=2^{(a,n)}-1=2^a-1\)

\(\therefore 2^a-1|2^n-1\),矛盾，得证

定理3.2唯一分解定理

可行性：

当\(n=2\)时，可分解。

若\(n=2,3,....,k\)时均可分解，当\(n=k+1时\)

• 1.\(k+1\)时质数——自身就是分解

• 2.一定有\(k+1=ab\)，从\(a,b\)的分解推过来

唯一性：

设\(n=p_1p_2....p_s=q_1q_2....q_t(s>=t)\)

\(\because p_1|q_1q_2....\)

\(\therefore p_1|q_i,等价于p_1|q_1\)

由此可得\(p_{t+1}p_{t+2}....p_{s}=1\),矛盾，得证。

定义3.3

定义\(v_p(n):n\)的标准分解式中所含质因子\(p\)的指数

\(v_p(n1n2)=vp(n1)+vp(n2)\)

\(v_p(gcd(n1,n2))=min(v_p(n1),v_p(n2))\)

\(v_p(lcm(n1,n2))=max(v_p(n1),v_p(n2))\)

\[v_p(n1+n2)= \begin{Bmatrix} min(v_p(n1),v_p(n2))(v_p(n1)\ne v_p(n2)) \\ >=v_p(n1)=v_p(n2) \end{Bmatrix}\]

\(v_p(n!)=\sum_{i=1}^{\infty } \left \lfloor \frac{n}{p^i} \right \rfloor\)

\(v_p(C_{n}^{m})=\sum_{i=1}^{\infty } \left \lfloor \frac{n}{p^i} \right \rfloor-\left \lfloor \frac{m}{p^i} \right \rfloor-\left \lfloor \frac{n-m}{p^i} \right \rfloor\)

最下面式子的含义正好是\(n+(n-m)\)在\(p\)进制下的进位个数

推论3.4

设正整数n的标准分解式为\(:n=p1^{e_1}p2^{e_2}...pk^{e_k}\)

设\(m=p1^{f_1}p2^{f_2}...pk^{f_k}\),则\(m|n\Rightarrow f_i<=e_i(1<=i<=k)\)

因数个数公式：

\[\tau (n)=(e_1+1)(e_2+1)....(e_k+1) \]

因数和公式：

\[\sigma(n)=\frac{p_1^{e_1+1}-1}{p_1-1} \frac{p_2^{e_2+1}-1}{p_2-1}.... \frac{p_k^{e_k+1}-1}{p_k-1} \]

因数积公式：

\[n^{\frac{\tau (n)}{2} } \]

eg1:

证明\(6|n^3+5n\)
\(n^3+5n=n^3-n+6n=(n-1)n(n+1)+6n\)

eg2:

设\(a,b,c,d\)是正整数，满足\(a^5=b^4,c^3=d^2,c-a=19\)，求\(d-b\)
设\(a^5=b^4=m^20,c^3=d^2=n^6\)
\(\therefore a=m^4,b=m^5,c=n^2,d=n^3\)
\(\because c-a=19\)
\(\therefore n^2-m^4=19\)
\(\therefore (n+m^2)(n-m^2)=19\)
\(\therefore n=10,m=3\)
\(\therefore d-b=757\)

eg3:

已知\(p\)为质数，\(x,y\)为正整数，求解方程\(p^x=y^3+1\)
\(y^{3}+1=(y+1)\left(y^{2}-y+1\right)\)
\(特判其中一个是一解得 y=1, p=2, x=1\)
\(\operatorname{gcd}\left(y+1, y^{2}-y+1\right)=\operatorname{gcd}(y+1,3) (辗转相除法)\)
\(故 p=3 ，解得 x=3, y=3\)

定理3.7

设正整数\(m,n\)的标准分解式为：\(m=p_1^{f_1}p_2^{f_2}....p_k^{f_k},n=p_1^{g_1}p_2^{g_2}....p_k^{g_k}\)

• 1.最大公因数：\((m,n)=p_1^{min(f_1,g_1)}p_2^{min(f_2,g_2)}....p_k^{min(f_k,g_k)}\)
• 2.最小公倍数：\([m,n]=p_1^{max(f_1,g_1)}p_2^{max(f_2,g_2)}....p_k^{max(f_k,g_k)}\)

推论3.8

• 1.\((ma,mb)=m(a,b)\)
  显然，就不证明了
• 2.\((a,uv)=(a,(a,u)v)\)
  \(右式=(a,(av,uv))\)
  \(根据性质2.6，(a,(av,uv))=((a,av),uv)=(a,uv)=左式\)，得证
• 3.\((u,v)=1 \Rightarrow (a,uv)=(a,u)(a,v)\)
  \(u,v\)无公因数，分开结果一样
• 4.\((a,b)=1,(c,d)=1\Rightarrow (ab,cd)=(a,c)(a,d)(b,c)(b,d)\)
• 5.\((a,b)=1\Rightarrow (a^k,b^k)=1\)
  可以参考质因数分解理解

定义4.1同余

\(n|a-b\Rightarrow a\equiv b(\bmod n)\)

性质4.2同余的性质

• 1.若\(a\equiv b(\bmod n)\),则\(a\)与\(b\)对\(n\)作带余除法所得的余数相同
• 2.自反性：\(a\equiv b(\bmod n)\Rightarrow b\equiv a(\bmod n)\)
• 3.传递性：\(a\equiv b(\bmod n),b\equiv c(\bmod n)\Rightarrow a\equiv c(\bmod n)\)
• 4.可加减性：\(a_1\equiv a_2(\bmod n)，b_1\equiv b_2(\bmod n)\Rightarrow a_1\pm b_1\equiv a_2\pm b_2\)
• 5.可乘性：\(a_1\equiv a_2(\bmod n)，b_1\equiv b_2(\bmod n)\Rightarrow a_1\pm b_1\equiv a_2\pm b_2\)
• 6.可除性：\(ka\equiv kb(\bmod kn)\Rightarrow a\equiv b(\bmod n)\)，不能直接除
• 7.互质可除性：\(ka\equiv kb(\bmod n),(k,n)=1\Rightarrow a\equiv b(\bmod n)\)

例子4.3：

eg1:

已知\(n=12345678910...20212022\),求\(n除以11的余数\)
\(n \equiv 123456789+1011....99+100....999+1000....2022\equiv 5+(10+....+99)+(999-998+....+101-100)+(1001+....+2022\equiv 5+10+10 \equiv 3)\)

eg2:

求证:\(1984|993^{993}+991^{991}\)
\(993^{993}+991^{991}\equiv 993^{993}+(-993)^{991}\equiv 993^{991}(993^2-1)\equiv 993^{991}(993+1)(993-1)\equiv 993^{991} \times 497 \times 2 \times 992 \equiv 0\),得证。

定理4.4费马小定理

内容：\(若p是质数，a是任意一个数，则有a^p\equiv a(\bmod p)\)

• 1.\(a是p的倍数\)，显然
• 2.\(a不是p的倍数\)
  原命题等价于\(a^p-a是p的倍数\)
  令\(b=a-1\)
  \(\therefore a^p-a=(b+1)^p-(b+1)=b^p+C_{p}^1b^{p-1}+....+C_{p}^{p-1}b+1-b-1(二项式定理)\)
  \(\equiv b^p-b(\bmod p)\)
  \(\therefore 若b^p\equiv b(\bmod p)成立，b+1^p\equiv b+1(\bmod p)成立\)
  相信看到这里的读者都想到了数学归纳法。
  \(\because 1^p\equiv 1(\bmod p)\)
  \(\therefore a^p\equiv a(\bmod p)成立\)
  但是注意：有的合数\(p\)也满足费马小定理(卡迈尔数)，但是很少，所以费马小定理可以作为一个检验质数的标准

定义5.1

剩余类：

把\(\mathbb{z}按照\bmod n\)分为\(0(\bmod n),1(\bmod n)....n-1(\bmod n)\)
\(\mathbb{z_n}=\){\(\overline{0}, \overline{1},.... \overline{n-1}\)}
\(\overline{a}+\overline{b}=\overline{a+b}\)
\(\overline{a}-\overline{b}=\overline{a-b}\)
也可以乘，但除可能无解。

完全剩余系（完系）：

\(x=\){\(a_i \in \overline{i}|0<=i<=n-1\)}
那么显然\(y=\){\(b_i|b_i=a_i+k,k \in \mathbb{N}\)}也是一个完全剩余系
\(z=\){\(b_i|b_i=a_i\times k,k \in \mathbb{N},且gcd(k,n)\)}也是一个完全剩余系

既约剩余系：

也称简化剩余系或缩系，是m的完全剩余系中与m互素的数构成的子集，如果模m的一个剩余类里所有数都与m互素，就把它叫做与模m互素的剩余类。在与模m互素的全体剩余类中，从每一个类中各任取一个数作为代表组成的集合，叫做模m的一个简化剩余系。

欧拉函数：

\(\varphi(n)=0到n-1中与n互质的数的个数\)
积性：\(m,n互质\Rightarrow \varphi(n)\times \varphi(m)=\varphi(nm)\)
计算欧拉函数可以积性证明，也可以考虑容斥：
$令数列 p 为唯一分解后 n 的质因子数列， k 为质因子数， A_{i} 为 p_{i} 倍数个数 则 \varphi(n)=n-\left|\bigcup_{i=1}^{n} A_{i}\right|=n \prod_{i=1}^{k}\left(1-p_{i}\right) $

逆元：

若\(a\times b \equiv 1(\bmod n)\),则称\(b为a在\bmod n意义下的逆元(a^{-1}=b)\)，且\(b在\bmod n意义下唯一\)

证明：

1.裴蜀定理可以证明存在性：
\(\forall x,y\)使\(ax+yn=1\)
\(\therefore ax \equiv 1(mod n)\)
2.存在和唯一可以一起证明：
{\(0,1,...,n\)}是完系，\(\times a\)还是一个完系而且完系中\(b \in \overline{1}\)是唯一的

性质：

• 1.\(a {\div} b=a^b{-1}\)

---

而且对于任意质数\(p\)其完系\(Z_p\)是四则运算封闭的。

例题：

eg1:

证明：\(p\)为奇质数，若\(1+\frac{1}{2}+....+\frac{1}{p-1},(m,n)\)，则\(p|m\)
原式\(=(1+\frac{1}{p-1})+(\frac{1}{2}+\frac{1}{p-2})+...\),此时每个括号内通分分子为\(p\)，得证

eg2:

求\(C_{100}^{73} (\bmod 101)\)
\(C_{100}^{73}=\frac{100!}{73!27!}\equiv 100!(73!27!)\equiv 100!(73!(-1)^{27}74\times 75.....\times 100)^{-1}\equiv 100!(-(100!))^{-1}\equiv -1\)
同理可得\(C_{p-1}^{m} \equiv (-1)^m (\bmod p)\)
还有一个性质：$C_{n}^{p}=\left \lfloor \frac{n}{p} \right \rfloor $，但作者太拉不会证

定理5.2中国剩余定理：

已知\(n_1,n_2,...,n_k\)两两互质，同余方程组：

\[\begin{Bmatrix} x\equiv a_1(\bmod n_1) \\ x\equiv a_2(\bmod n_2) \\ ... \\ x\equiv a_n(\bmod n_k) \end{Bmatrix}\]

在模\(n=n_1n_2....n_k\)的意义下有唯一解。
举个例子：

\[\begin{Bmatrix} x\equiv a_1(\bmod 3) \\ x\equiv a_2(\bmod 5) \\ x\equiv a_3(\bmod 7) \end{Bmatrix}\]

对于这个问题有一个奇妙的解法。考虑如果条件是被3,5,7整除，问题就很好做。求出最小公倍数即可。显然这个数可以是105的任意倍。

如果条件是除以3余1，被5和7整除，问题也很好做，在被5,7整除的数中找一个除以3余1的，易知最小满足要求的数是70。同理除以5余1，被3和7整除的最小数是21，理除以7余1，被3和5整除的最小数是15.

除以3的余数	除以5的余数	除以7的余数	最小满足要求的数
0	0	0	105
1	0	0	70
0	1	0	21
0	0	1	15

考虑第二行，70除以3余1，被5,7整除，那么显然140也被整除，而除以3的余数变成了2，正好是70的两倍。

如果再把140加上21呢（也就是161），因为21被3和7整除，所以161除以3和7的余数和140的一样，除以5的余数则是变成了21的1。

有一个显然的结论，一个大于105的数，减去105后，除以3,5,7的余数不会发生改变。所以35和140除以3,5,7的余数一样，56和161除以3,5,7的余数也一样。

除以3的余数	除以5的余数	除以7的余数	满足要求的数
2	0	0	140
2	1	0	161

除以3的余数	除以5的余数	除以7的余数	最小满足要求的数
2	0	0	35
2	1	0	56

可以归纳出通解：
\(设 M_{i}=\frac{n_{1} n_{2} n_{3} \cdot n_{k}}{n_{i}}\)
\(解为 x \equiv \sum_{i=1}^{k} a_{i} M_{i} M_{i}^{-1} ，其中的逆元是 \bmod 对应的 n_{i} 的逆\)

定义5.3素数域

记得开头的话吗，数论只关心整数，所以怎么在整数里定义类似除法的运算?
首先\(a{\div} b\),可以理解为\(a\times b^{-1}\),关键就在找到\(b的逆元\),而这在完全剩余系里非常好理解，下面是一个\(\bmod 7\)的完全剩余系：

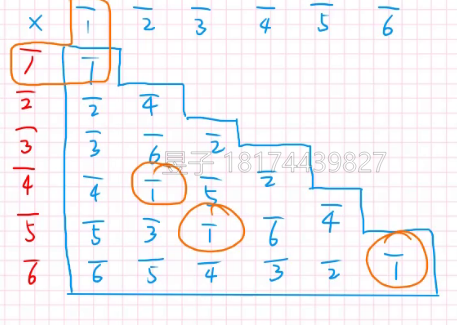
现在有逆元了，比如\(\overline{4}^{-1} = \overline{2}\)
计算一个式子帮助理解：
\(\overline{5} {\div}\overline{4}=\overline{5} \times \overline{2}=\overline{3}\)
为什么叫素数域，因为你考虑每个元素都要有逆元，只能是素数了。

定义6.1数论函数

定义域是整数的函数

定义6.2积性函数和完全积性函数

充要判定条件：
积性函数：

\[\begin{Bmatrix} f(n)=f(p_1^{e_1})....f(p_m^{e_m}) \\ f(1)=1 \end{Bmatrix}\]

完全积性函数：

\[\begin{Bmatrix} f(n)=f(p_1)^{e_1}....f(p_m)^{e_m} \\ f(1)=1 \end{Bmatrix}\]

易知：3.4的因数个数公式，因数个数公式；5.1的欧拉函数都是积性函数