逻辑，集合，映射与计数

1.逻辑

命题：能够判断正确或错误的叙述。

复合命题：若\(p\),则\(q\)

设原命题为若\(p\),则\(q\)，则：

• 1.逆命题：若\(q\),则\(p\)
• 2.否命题：若\(\neg p\),则\(\neg q\)
• 3.逆否命题：若\(\neg q\),则\(\neg p\)

其中原命题与逆否命题等价，逆命题与否命题等价。

条件：

若 \(p \Rightarrow q\) ,则 \(p\) 是 \(q\) 的充分条件，\(q\) 是 \(p\) 的必要条件。

p是q的充分不必要条件	\(p \Rightarrow q\)且\(q \nRightarrow p\)
p是q的必要不充分条件	\(p \nRightarrow q\)且\(q \Rightarrow p\)
p是q的充要条件	\(p \Rightarrow q\)且\(q \Rightarrow p\)
p是q的既不充分也不必要条件	\(p \nRightarrow q\)且\(q \nRightarrow p\)

量词：

• 1.全称量词：任意，符号为$\forall $
• 2.存在量词：存在，符号为$\exists $

eg1.\(\forall x \in R,有 f(x) > k\)

很典型的题目，可以转化为\(max(f(x))>k\)

eg2.\(\exists x \in R,有 f(x) > k\)

存在一个\(x\)满足条件即可，转化为\(min(f(x))>k\)

2.集合，元素

• 1.集合元素的三个特征：无序性，互异性，确定性
• 2.元素与集合之间的关系是属于或不属于，用\(\in\)或$\notin $表示
• 3.常见的集合记法：

集合	自然数集	正整数集	整数集	有理数	实数集
符号	\(N\)	\(N^{* }\)或\(N_{+}\)	\(Z\)	\(Q\)	\(R\)

ps:在符号上加$ * ,+$的上下标通常表示正的部分

集合与元素间的基本关系

若\(a\)属于集合\(A\)，记作\(a \in A\),若\(a\)不属于集合\(A\)，记作\(a \notin A\)

集合与集合间的基本关系

子集：

集合\(A\)包含于集合\(B\)(集合\(A\)是集合\(B\)的子集)，记作\(A\subseteq B\),也可以记作\(B \supseteq A\)
下面我们用数学语言解释\(A\subseteq B\)：
\(\forall x \in A\),均有\(x \in B\)。
从这条解释可以看出\(A\subseteq B\)可以得出\(x \in A\)是\(x \in B\)的充分条件，\(x \in B\)是\(x \in A\)的必要条件
\(Venn\)图:

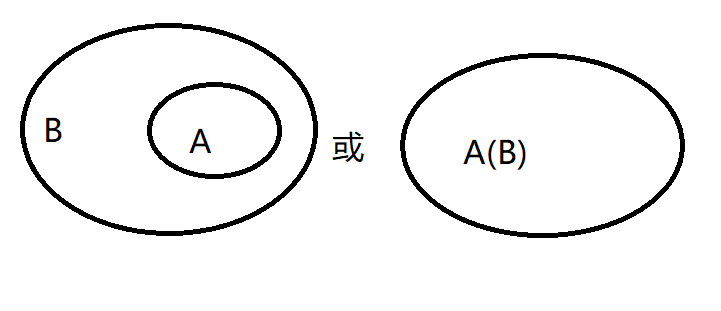
真子集：

集合\(A\)是集合\(B\)的子集，且集合\(B\)中至少有一个元素不在集合\(A\)中
\(Venn\)图:

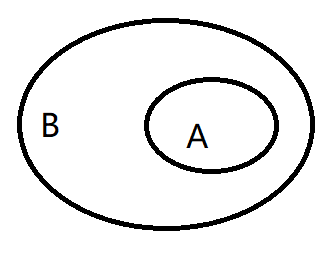
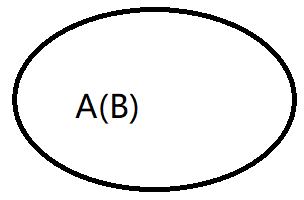
集合相等：

如果有\(A\subseteq B\)，\(B\subseteq A\)，称\(A=B\)
\(Venn\)图:

集合与集合间的基本运算

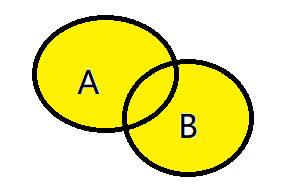
集合的并集：

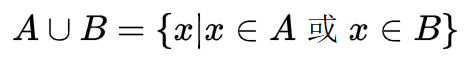
图像（黄色部分）：

n个集合\(A_1,A_2....A_n\)的并集可以记作\(\bigcup_{i=1}^{n} A_i\)

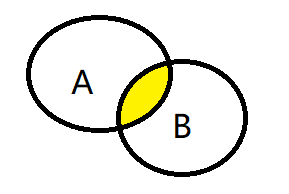
集合的交集：

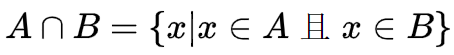
图像：

n个集合\(A_1,A_2....A_n\)的交集可以记作\(\bigcap_{i=1}^{n} A_i\)

集合的补集：

要谈补集，我们首先要钦定一个全集\(U\),\(U\)里包含了所有讨论的元素。

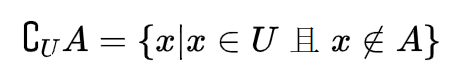
图像：

集合相乘：

就是笛卡尔积,没什么好说的。

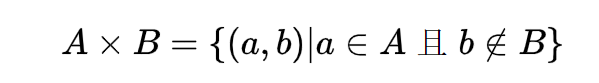
幂函数：

\(2^{A}\)={\(A\)的所有子集}

集合的运算律：

• 1.\(A \cup (B \cap C)=(A\cup B)\cap (A \cup C)\)

证明：

\(\forall x \in A \cup (B \cap C)\)

<1>若\(x \in A\),则\(x \in (A\cup B),x \in (A \cup C)\)

\(\therefore x \in (A\cup B)\cap (A \cup C)\)

<2>若\(x \in (B \cap C)\),则\(x \in B,x \in C\)

\(\therefore x \in (A \cup B),x \in (A \cup C)\)

\(\therefore x \in (A\cup B)\cap (A \cup C)\)

综上，\(A \cup (B \cap C)\subseteq (A\cup B)\cap (A \cup C)\)

\(\forall x \in (A\cup B)\cap (A \cup C)\)

\(\therefore x \in A\)

\(\therefore x \in A \cup (B \cap C)\)

\(\therefore (A\cup B)\cap (A \cup C) \subseteq A \cup (B \cap C)\)

\(\therefore (A\cup B)\cap (A \cup C) = A \cup (B \cap C)\)

---

• 2.\(A \cap (B \cup C)=(A \cap B) \cup (A \cap C)\)

证明：

\(\forall x \in A \cap (B \cup C)\)

\(\therefore x \in A,x \in (B \cup C)\)

\(\therefore x \in A,x \in B,x \in C\)

\(\therefore x \in (A \cap B) \cup (A \cap C)\)

\(\therefore A \cap (B \cup C)\subseteq (A \cap B) \cup (A \cap C)\)

\(\forall x \in (A \cap B) \cup (A \cap C)\)

<1>\(x \in (A \cap B)\)

\(\therefore x \in A,x \in B\)

\(\therefore x \in (B \cup C)\)

\(\therefore x \in A \cap (B \cup C)\)

<2>\(x \in (A \cap C)\)

\(\therefore x \in A,x \in C\)

\(\therefore x \in (B \cup C)\)

\(\therefore x \in A \cap (B \cup C)\)

综上，$ (A \cap B) \cup (A \cap C)\subseteq A \cap (B \cup C)$

\(\therefore (A \cap B) \cup (A \cap C)= A \cap (B \cup C)\)

映射

有\(A,B\)两个非空集合，若果按照某种确定的对应关系\(f\),使得对于集合\(A\)中任意的一个元素\(x\),在集合\(B\)中都有唯一确定的元素\(f(x)\)与之对应，称为\(f:A\to B\)

在\(f:A \to B\)中，\(x\)的取值范围\(A\)为映射的定义域，\(f(x)\)为\(x\)在映射\(f\)下的象集合\(f(x)=\){\(f(x)|x \in A\)}

单射：

若对于\(\forall x_1 \in A,x_2 \in A\),均满足\(f(x_1)\ne f(x_2)\),称映射\(f\)为单射。

满射：

若\(f(A)=B\),则称映射\(f\)为满射。

一一对应：

若映射\(f\)，既是单射也是满射，称映射\(f\)为一一映射，存在\(f^{-1}:B \to A\)(反函数)，使得:

• 1.\(\forall x \in A\),均有\(f^{-1}(f(x))=x\)
• 2.\(\forall y \in B\),均有\(f(f^{-1}(y))=y\)

构造映射：

\(eg1.\)构造一个一一映射\(f:\)整数集\(\to\)偶数集

\(\forall x \in Z,f(x)=2 \times x\)

\(eg2.\)构造一个一一映射\(f:\)正整数集\(\to\)整数集

\(f(1)=0,f(2)=1,f(3)=-1......\)

\(eg3.\)构造一个一一映射\(f:\)正整数集\(\to\)有理数集

这个对应有点难度，先自己想一想。
先把\(0\)单独考虑，现在每一个有理数可以对应一个最简分数$\frac{p}{q} \(,我们把每个有理数对应一个二元组\)(p,q)$,放到直角坐标系中，形成下图（先只考虑大于\(0\)的有理数）：

我们从\((1,1)\)开始，蛇行向上对应，如果不是最简分数就跳过：

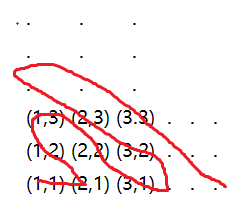
怎么对应负有理数呢，一正一负就行了。

\(eg4.\)是否能构造一个一一映射\(f:\)正整数集\(\to\)实数集

先自己试着构造试试。
不难发现根本不可行，下面是证明：
反证法：
若{\(a_1,a_2,......,a_n,......\)}\(=R\)
取一个实数\(x\)使得:

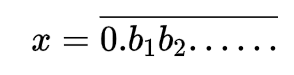
其中\(b_i \ne a_i\)的第\(i\)位小数。显然\(x\ne a_1,x\ne a_2,.....\)但\(x \in R\),与条件矛盾。

应用：

• 1.\(C_n^{k}=\frac{n!}{k!(n-k)!}\)
  首先有\(A_n^{k}=\frac{n!}{(n-k)!}\)
  试图构造一个从\(A_n^k\)到\(C_n^k\)的映射，发现有很多个排列对应一个组合。
  排列的长度是\(k\),那么自然有\(k!\)个排列对应一个组合，所以组合数的公式是\(\frac{A_n^k}{A_k^k} =\frac{n!}{k!(n-k)!}\)
• 2.\(C_n^{k}=C_n^{n-k}\)
  很好理解。当然你可以列出这两个的公式也可以构造一一对应（对应补集）
• 3.\(C_n^0+C_n^1+....+C_n^n=2^n\)
  你考虑这其实就是子集个数。

实际应用：

\(eg1.1000\)瓶药水中有一瓶有毒，每次可以取出若干瓶药水混合在一起检验是否有毒。问找到有毒的药水至少需要多少次操作。

这个问题的答案其实不难，10次，但是包含了一些思想。

---

二分法：最简单的方案，有一个问题，每次操作依赖于前一次操作的结果，若果等待前一次结果的时间很长，这就不是理想的方案。

---

二进制法：给每一瓶药水二进制编号，不会超过\(10\)位，第\(i\)次操作取二进制从前往后第\(i\)位为\(1\)的药水一起检验，\(10\)次的结果有毒记为\(1\),无毒记为\(0\)，把这十个数字放在一起形成一个二进制数，对应会编号即可。正确性是显然的

---

更深入一点思考为什么至少要进行\(10\)次操作，我们其实是在建立每一组操作结果与有毒药水编号之间的一一对应，假设进行\(9\)次操作，只有\(512\)个操作结果，无法一一对应\(1000\)个药水编号

计数

容斥原理

忘记介绍一种符号了，\(\left | A \right |\) 代表\(A\)集合中的元素个数。
容斥原理的内容：$\left | \bigcup_{i=1}^{n}A_i \right | =\sum_{i=1}^{n}\left | A_i \right | -\sum_{1<=i<j<=n}\left | A_i\cap A_j \right |+......+(-1)^{n-1}\left | A_1\cap A_2\cap ......\cap A_n \right | $

证明：
\(\forall x \in \bigcup_{i=1}^{n}A_i\)在等式左边计算一次
设\(x \in A_{i1},x \in A_{i2},......,x \in A_{ik}\),令\(S\)为\(x\)在右式的计算次数，则：
\(S=C_{k}^{1}-C_{k}^{2}+......+(-1)^{k}C_{k}^{k}\)
根据二项式定理:\((1+y)^{k}=C_{k}^{0}+C_{k}^{1} \times y+......+C_{k}^{k} \times y^{k}\)
令\(y=-1\),得：\(0=1-S,S=1\)
\(\therefore x\)在等式右边被计算一次，等式成立。

错排

通项：

根据容斥，错排的个数是全排列减去一个位置对的加上两个位置对的......
即：\(n!-C_{n}^{1} \times (n-1)!+C_{n}^{2} \times (n-2)!+......+(-1)^{n-1}C_{n}^{n}\)
\(=\sum_{i=0}^{n}(-1)! \times C_{n}^{i} \times (n-i)!\)
\(=\sum_{i=0}^{n}(-1)! \times \frac{n!}{i!(n-i)!} \times (n-i)!\)
\(=\sum_{i=0}^{n}(-1)! \times \frac{n!}{i!}\)
\(=n! \times \sum_{i=0}^{n}(-1)! \times \frac{1}{i!}\)
由\(e^{x}=1+\frac{x}{2!}+\frac{x^{2}}{3!}......\),此时令\(x=-1\)
\(\therefore e^{x}=1-\frac{1}{2!}+\frac{1}{3!}......\)，和错排的公式谜之相似，只不过是无限项，误差小于\(\frac{1}{n+1}\)
记录\(n\)个数的错排数为\(D_n,D_n\approx \frac{n!}{e}\)

递推：

\(D_n=(n-1)(D_{n-2}+D_{n-1})\)
我们假设\(1\)对应\(2\)(其他也是一样的，\(\times n-1\)就好了)，那么面临两种情况：

• 1.2对应1
  此时后面的数形成一个\(n-2\)的错排
• 2.2不对应1
  这时后面总有一个数\(k\)对应\(1\),令\(k\)对应\(2\)，对结果没有影响，这时形成一个\(n-1\)的错排

数字和固定的五位数

原问题：

数字和为6的五位数共有多少个？

很经典的插板法，记这个五位数为\(abcde\)
由题：\(a+b+c+d+e=6\),此时\(b,c,d,e\)可以为\(0\)，每一个加上\(1\),新的数是\(a(b+1)(c+1)(d+1)(e+1)\)。
\(a+(b+1)+(c+1)+(d+1)+(e+1)=10\)，插板法就可以（不可能分出来一个10以上的数），答案是\(C_9^4\)
趁机推销自己的插板法博客:组合数学初步

change 1:

数字和为40的五位数共有多少个？
\(把\overline{abcde}对应成\overline{(10-a)(10-b)(10-c)(10-d)(10-e)}\)，然后老操作，还是\(C_9^4\)

差分：

定义\(\bigtriangleup h_n=h_{n+1}-h_n\)
不难看出若\(\forall x \in n ,\bigtriangleup ^2h_x=0\)（先差分一次，再在差分数组上差分一次），{\(h_n\)}为等差数列。
同样的，若\(\forall x \in n ,\bigtriangleup ^3h_x=0\)，{\(h_n\)}为平方数数列。
更进一步的，我们发现每进行一次差分，原式的次数减一。
差分的优美性质还在于是线性算子：
\(\bigtriangleup (a_n+b_n)=\bigtriangleup a_n+\bigtriangleup b_n\)