20230801

前文：离散概率论2

概率密度函数

我们已经了解了基本离散概率论，可对于一个连续型随机变量。比如在R上取值，这个时候我们就需要概率密度函数。
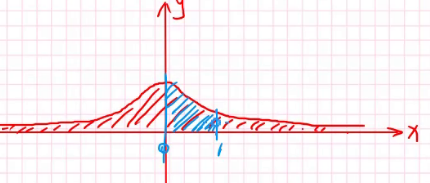
我们先拿一个经典的正态分布图像：

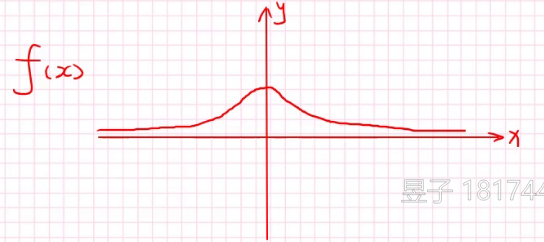
显然任意类似于P(x=1)的值都是0，但我们可以研究X在某一个区间上的概率了，比如：

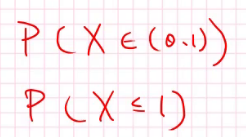
可概率密度函数怎样体现概率，通俗的来说就是与x轴围成的图形面积为1，也就是：

等价于离散概率论中的：

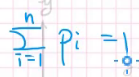
所以它的计算也不难，比如X属于(0,1)的概率就是：

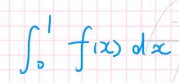
在图上就是蓝色部分的面积：

分布函数：

分布函数：\(F(x)=P(X<=x)\)
有没有发现和前缀和迷之相似。
分段函数不论变量是离散还是连续都是可以刻画的，先自己画一个离散的试试？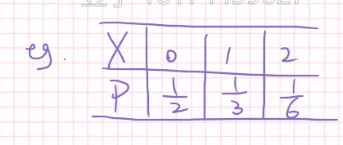
分布函数长这样：

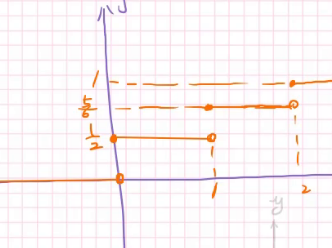
而连续的随机变量分布函数的算式也不难得出：

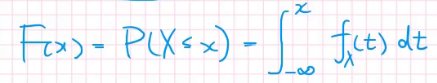
大数定律：

频率收敛到概率。这是显然的。
现在介绍的是一种弱大数律：khinchine大数律。
设\(X_n\)为独立同分布的随机变量序列，若\(E(X_n)\)为小于正无限的定值则有：

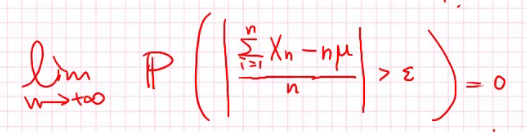
解释一下：

• 1.独立同分布：在概率统计理论中，指随机过程中，任何时刻的取值都为随机变量，如果这些随机变量服从同一分布，并且互相独立，那么这些随机变量是独立同分布。
• 2.$\varepsilon $是一个接近\(0\)的正数

均匀分布：

字面的意思，记作\(X~u(a,b)\),满足：

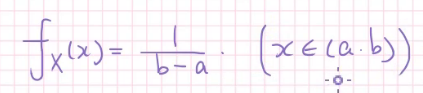
什么，你说为什么记作u?
\(uniformly\) 均匀的，另一个角度上，它的概率密度函数就是平的：

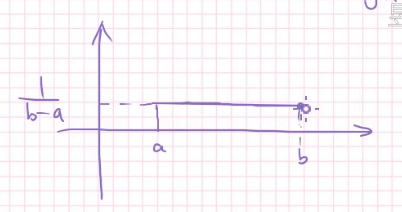
正态分布：

记作:

我们看一下它的概率密度函数：

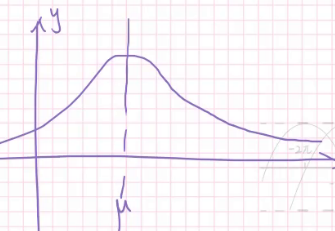
发现了吗？概率密度在$\mu $两侧对称并逐渐递减。当然你也可以算出它的具体值（只要你想）：

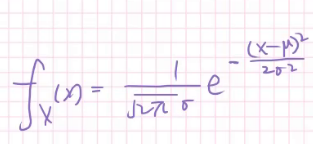
随机数：

首先，我们要承认一件事：

• 1.真随机数只能物理发生；任何程序实现的伪随机数
• 2.真随机数是均匀，无周期的；伪随机数是有周期的
  为什么物理能发生真随机数？或许你听过测不准原理或杨氏双缝干涉实验（不知道可以查一查，主要是因为物质具有波的性质）

而电脑生成随机数有两个要点：

• 1.seed好，保密（知道seed就知道结果）
• 2.周期长（局部看起来随机）

但如果我现在不想让随机数均匀分布，而是形成分布函数。

显然对于一个(0,1)的均匀分布，有\(P(R<=x)=x\)（R是(0,1)上的一个均匀分布）。

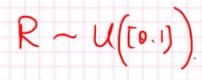
我们考虑计算F的反函数<=x的概率：

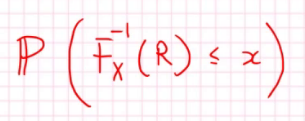
两边同乘F：

我们知道\(P(R<=x)=x\)，所以这个式子就是:

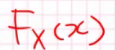
这个想法不仅对均匀分布可以做，两点分布也可以（有时候要求广义逆）

随机算法：

Sherwood算法

这个算法使用于一些不稳定的算法（最坏时间复杂度和均摊时间复杂度相差很大）。
比如快速排序，每一次随机基准，乱排分成的左右两边，这有效避免了极端情况。

LasVegas算法

通过多次随机找到最佳解。

Monte Carlo算法

通过多次随机减小误差。比如下面的例子：

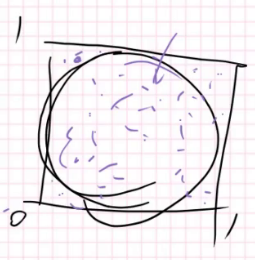
边长为1的正方形中有一个圆，求圆的面积。对于这个问题我们可以随机向正方形里扔点，圆的面积和正方形面积的比值就是园内的点/所有点