并查集
简述
并查集其实是一个很有用的算法(至少我是这么认为的),很简单,代码也很好写,今天突然想写一下并查集。
直接讲并查集不太好说,我们先看下面这一道题:
洛谷 P3367 【模板】并查集
【模板】并查集
题目描述
如题,现在有一个并查集,你需要完成合并和查询操作。
输入格式
第一行包含两个整数 \(N,M\) ,表示共有 \(N\) 个元素和 \(M\) 个操作。
接下来 \(M\) 行,每行包含三个整数 \(Z_i,X_i,Y_i\) 。
当 \(Z_i=1\) 时,将 \(X_i\) 与 \(Y_i\) 所在的集合合并。
当 \(Z_i=2\) 时,输出 \(X_i\) 与 \(Y_i\) 是否在同一集合内,是的输出
Y ;否则输出 N 。
输出格式
对于每一个 \(Z_i=2\) 的操作,都有一行输出,每行包含一个大写字母,为 Y 或者 N 。
样例 #1
样例输入 #1
4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4
样例输出 #1
N
Y
N
Y
提示
对于 \(30\%\) 的数据,\(N \le 10\),\(M \le 20\)。
对于 \(70\%\) 的数据,\(N \le 100\),\(M \le 10^3\)。
对于 \(100\%\) 的数据,\(1\le N \le 10^4\),\(1\le M \le 2\times 10^5\),\(1 \le X_i, Y_i \le N\),\(Z_i \in \{ 1, 2 \}\)。
转化
合并两个集合有什么性质呢?我们可以把每一个集合看成一棵树中的节点,把两个集合合并其实就是把两棵树合成一棵。而两个集合在同一棵树中就代表了在一个大集合中。
find函数
可我怎么知道两个集合在不在同一棵树中呢?仔细思考一下,我们需要找到一棵树中所有点的共同特征,同时这个特征要便于维护。建议新手先看着下面的树自己思考。
(这个树上节点的信息是集合,没有采用树上左右儿子的编号方法)
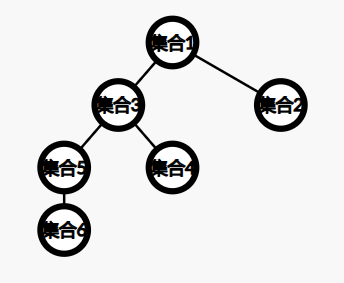
根节点一样!是不是恍然大悟?求一个节点所在的树的根节点很简单,一直跳它的父亲就行了(所有节点一开始的父亲是自己,所以跳到节点为自身的节点就找到根节点了)。
对于求一个节点所在树的根节点,我们使用以下代码:
不要贺代码哟
int find(int xx){//没有优化的find函数
if(xx==fa[xx]) return xx;//fa[xx]为xx的父亲
else return find(fa[xx]);
}
状态压缩:
为什么代码里写的是“没有优化的find函数”,因为你考虑树其实还好,但如果退化成了一条链,每一次询问都要从最底下找到最上面,时间就爆炸了。
怎么优化呢?你考虑这样一件事,就是你只关心根节点,并不关心中途的祖先,那对于一次find的调用,我们可以把中途的所有点都直接连向根节点,这样下次就可以直接一次到根节点了。
状态压缩后的上图:
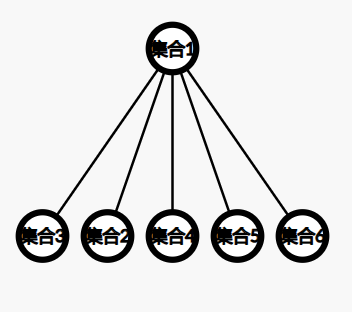
ps:状态压缩不能维持所有父子关系,对于要求记录父子关系的题目不适用
优化后的find函数
点击查看代码
int find(int xx){
if(fa[xx]==xx) return xx;
else return fa[xx]=find(fa[xx]);
}
\(z_i=2\)的代码
对于这道题,\(z_i=2\)就可以愉快地解决了:
点击查看代码
if(z==2){
int x,y;
cin>>x>>y;
if(find(x)==find(y)) cout<<"Y"<<endl;
else cout<<"N"<<endl;
}
合并(\(z_i=1\))
考虑两棵树的合并,不难理解,我们肯定是把一棵树的根节点\((find(x))\)接到另一棵树的根节点上\((find(y))\)。
点击查看代码
void unionn(int x,int y){
x=find(x);//x所在树的根节点
y=find(y);//y所在树的根节点
fa[x]=y;
}
全代码:
不要抄袭
#include<bits/stdc++.h>
using namespace std;
int n,m;
int z,x,y;
int fa[10001];
int find(int x){
if(fa[x]==x) return x;
else return fa[x]=find(fa[x]);
}
void unionn(int x,int y){
x=find(x);
y=find(y);
fa[x]=y;
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
fa[i]=i;
}
for(int i=1;i<=m;i++){
cin>>z>>x>>y;
if(z==1){
unionn(x,y);
}
else{
if(find(x)==find(y)){
cout<<"Y"<<endl;
}
else{
cout<<"N"<<endl;
}
}
}
return 0;
}
扩展域并查集简介:
一般的并查集大小只有n,可是对于一些更加复杂的关系,一般的并查集就有些乏力。这时候我们以常数倍的空间付出代价。
例题:【ACWing】240. 食物链
背景:
动物王国中有三类动物\(A , B , C\),这三类动物的食物链构成了有趣的环形。
\(A\)吃\(B\),\(B\)吃\(C\),\(C\)吃\(A\)。现有\(N\)个动物,以\(1 ∼ N\)编号。
每个动物都是\(A , B , C\)中的一种,但是我们并不知道它到底是哪一种。有人用两种说法对这\(N\)个动物所构成的食物链关系进行描述:
第一种说法是”\(1 X Y\)”,表示\(X\)和\(Y\)是同类。
第二种说法是”\(2 X Y\)”,表示\(X\)吃\(Y\)。
此人对\(N\)个动物,用上述两种说法,一句接一句地说出\(K\)句话,这\(K\)句话有的是真的,有的是假的。
当一句话满足下列三条之一时,这句话就是假话,否则就是真话:
(1) 当前的话与前面的某些真的话冲突,就是假话;
(2) 当前的话中\(X\)或\(Y\)比\(N\)大,就是假话;
(3) 当前的话表示\(X\)吃\(X\),就是假话。
你的任务是根据给定的\(N\)和\(K\)句话,输出假话的总数。
输入格式:
第一行是两个整数\(N\)和\(K\),以一个空格分隔。以下\(k\)行每行是三个正整数\(D\),\(X\),\(Y\),两数之间用一个空格隔开,其中\(D\)表示说法的种类。若\(D = 1\),则表示\(X\)和\(Y\)是同类。若\(D = 2\),则表示\(X\)吃\(Y\)。
输出格式:
只有一个整数,表示假话的数目。
数据范围:
\(1 ≤ N ≤ 50000\)
\(0 ≤ K ≤ 100000\)
对该题的认知:
- 1.天敌的天敌是猎物
- 2.猎物的猎物是天敌
- 3.如果我们把同类看成是一个集合,那么它的天敌和猎物各是一个集合
扩展域并查集的思想:
我们不妨定义把元素个数提升至\(3*n\)个,对于原序列中的一个元素\(x\),定义\(x+n\)属于它的天敌,\(x+2*n\)属于它的猎物。
解法:
首先我们先把\(x>n,y>n\)判掉
说法1:
对于说法1。什么时候这句话是错的呢?因为\(y\)已经与\(x\)同类,所以就不能属于\(x\)的天敌或者猎物集合。
if(find(x+n)==y || find(x+2*n)==y){
ans++;//谎话数量
continue;
}
判断这句话正确后。\(x\)和\(y\)是同类,那么显然要把集合\(x\)和\(y\)合并,但容易忽略的是,因为\(x,y\)是同类,所以天敌,猎物也是一样的,也需要合并,所以操作是:
unionn(x,y);
unionn(x+n,y+n);
unionn(x+2*n,y+2*n);
说法2:
过于说法2.既然\(x\)是\(y\)的天敌,\(x\)自然不能是\(y\)的同类或猎物,也就是\(y\)不能是\(x\)的天敌或同类。
if(find(x)==find(y) || find(x+n)==find(y)){
ans++;
continue;
}
如果这句话正确,就将\(x\)与\(y\)的天敌合并,将\(x\)的天敌与\(y\)的猎物合并,将\(x\)的猎物与\(y\)合并。
unionn(x,y+n);
unionn(x+2*n,y+n);
unionn(x+n,y);
完整代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int fa[300001];
int n,k;
int ans;
int find(int xx){
if(fa[xx]==xx) return xx;
else return fa[xx]=find(fa[xx]);
}
void unionn(int xx,int yy){
xx=find(xx);
yy=find(yy);
fa[xx]=yy;
}
int main(){
cin>>n>>k;
for(int i=1;i<=3*n;i++) fa[i]=i;
while(k--){
int op,x,y;
cin>>op>>x>>y;
if(x>n || y>n){
ans++;
continue;
}
if(op==1){
if(find(x+n)==find(y) || find(x+2*n)==find(y)){
ans++;
continue;
}
unionn(x,y);
unionn(x+n,y+n);
unionn(x+2*n,y+2*n);
}
else if(op==2){
if(find(x)==find(y) || find(x+n)==find(y)){
ans++;
continue;
}
unionn(x,y+n);
unionn(x+n,y+2*n);
unionn(x+2*n,y);
}
}
cout<<ans;
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号