DP综合

DP是OI竞赛中应用特别广泛的一类算法 （通常我用来骗分打表）

下面进入正题

Part 1.01背包

01背包的题目要求通常是给你一些物品，每个物品有它的重量和价值，你有一定的空间来装这些东西，一种只有一个，问能拿走最多多少价值的物品。

01背包的解决方法很简单，对于每一个当前物品，我们都给它需要的空间，也获得它的价值，最后把所有情况比较求最大值。

对于代码来说，就是定义 \(f[i]\) 代表如果有 \(i\) 的空间最多能拿走的价值，用 \(w[i],v[i]\) 分别代表第 \(i\) 个物品的所占空间和价值,那么要放进当前物品，前面的物品最多也只能占 \(f[i-w[i]]\) 的空间，放进去的价值自然最多是 \(f[i-w[i]]+v[i]\) 把它和原来的 \(f[i]\) 比较去最大值就行了！也不用担心 \(i\) 之前的影响（正序枚举），因为之前讨论过了，下面是代码- - -

// C++ Version
for (int i = 1; i <= n; i++)
  for (int l = W; l >= w[i]; l--) f[l] = max(f[l], f[l - w[i]] + v[i]);

# Python Version
for i in range(1, n + 1):
    l = W
    while l >= w[i]:
        f[l] = max(f[l], f[l - w[i]] + v[i])
        l -= 1

Part 2.完全背包

完全背包和01背包非常像，唯一不同的区别是完全背包一件物品可以选很多次，所以它的转移方程很像，需要多一层循环 \(K\) 枚举第 \(i\) 件物品拿几个,下面是代码- - -

// C++ Version
#include <iostream>
using namespace std;
const int maxn = 1e4 + 5;
const int maxW = 1e7 + 5;
int n, W, w[maxn], v[maxn];
long long f[maxW];

int main() {
  cin >> W >> n;
  for (int i = 1; i <= n; i++) cin >> w[i] >> v[i];
  for (int i = 1; i <= n; i++)
    for (int l = w[i]; l <= W; l++)
      if (f[l - w[i]] + v[i] > f[l]) f[l] = f[l - w[i]] + v[i];  // 核心状态方程
  cout << f[W];
  return 0;
}

Part 3.区间DP

区间DP顾名思义就是枚举一段区间，大的区间由两个或多个区间合并（也就是转移过来，注意：把几段小区间合并成大区间大多数情况下是有代价的）通常对于一个 \(i\) 到 \(j\) 的区间，我们在 \(i\) 到 \(j\) 的范围内枚举一个 \(k\) 让 \(f[i][k]\) 和 \(f[k+1][j]\) 合并为 \(f[i][j]\) ，与原先的 \(f[i][j]\) 求最值。
(一维为左端点，第二维为右端点),下面是代码- - -

// C++ Version
#include<bits/stdc++.h>
using namespace std;
#define int long long
int a[305];
int sum[305];
int f[305][305];
signed main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        sum[i]=sum[i-1]+a[i];
        f[i][i]=0;
        for(int j=i+1;j<=n;j++) f[i][j]=1e9+7;
    }
    for(int len=1;len<=n;len++)
    {
        for(int i=1;i+len<=n;i++)
        {
            int j=i+len;
            int cost = 花费;
            for(int k=i;k<j;k++)
            {
                f[i][j] = min/max[j],f[i][k]+f[k+1][j]+cost);
            }
        }
    }
    printf("%lld\n",f[1][n]);
}

ps:小技巧，如果题目是一个环，可倍长求每个长度为N的最值合并。

Part 4.状压DP

状压DP顾名思义就是把一些不要用的状态去掉或将状态处理，使得降低时间或空间复杂度。
例如下面这道题：

Round Subset

题目描述

我们把一个数的 roundness 值定义为它末尾 \(0\) 的个数。

给你一个长度为 \(n\) 的数列，要求你从中选出 \(k\) 个数，使得这些选出的数的积的 roundness 值最大。

输入格式

第一行包括两个正整数 \(n\) 和 \(k\)（\(1 \leq n \leq 200\)，\(1 \leq k \leq n\)）。

第二行包括 \(n\) 个空白分隔的数 \(a_1,a_2,\ldots,a_n\)（\(1 \leq a_i \leq 10^{18}\)）。

输出格式

输出一个整数，是选择 \(k\) 个数并作积的最大 roundness 值。

样例解释

在第一个例子中，有三种选法。\([50,4]\) 的积是 \(200\)，roundness 值是 \(2\)；\([4,20]\) 的积是 \(80\)，roundness 值是 \(1\)；\([50,20]\) 的积是 \(1000\)，roundness 值是 \(3\)。

第二个例子中选法 \([15,16,25]\) 的积是 \(6000\)，roundness 值是 \(3\)。

第三个例子中所有的选法的积的 roundness 值都是 \(0\)。

translated by @poorpool

样例 #1

样例输入 #1

3 2
50 4 20

样例输出 #1

3

样例 #2

样例输入 #2

5 3
15 16 3 25 9

样例输出 #2

3

样例 #3

样例输入 #3

3 3
9 77 13

样例输出 #3

0

(不用教 \(0\) 是 \(2,5\) 相乘的结果吧？)

很快的，我们能想出 \(dp[i][j][k]\) 代表在前 \(i\) 位有 \(j\) 个 \(5\) ，\(k\) 个 \(2\) 可是空间代价太高，我们发现这是一个 \(bool\) 类型的数组，为什么不转化为 \(int\) ，那它的值不就代表了一维吗？首先第一维是没法省的，因为 \(5\) 的个数少，我们先把 \(5\) 给留下，它的值代表有多少个 \(2\) 不就行了？( \(2\)肯定是越多越好，代表的是当前情况下 \(2\) 的最多个数),代码如下---

#include<bits/stdc++.h>
using namespace std;

int n, k, ans;
int dp[205][6205];

long long num[205];
int two[205], five[205];

int main(){
	cin>>n>>k;
	for(register int i = 1; i <= n; ++i){
	    cin>>num[i];
		while(num[i] % 2 == 0){	
			++two[i];
			num[i] /= 2;
		}
		while(num[i] % 5 == 0){	
			++five[i];
			num[i] /= 5;
		}
	}
	memset(dp, -0x3f, sizeof(dp));
	dp[0][0] = 0; 
	for(int i = 1; i <= n; ++i)
		for(int j = i; j >= 1; --j)
			for(int p = 6200; p >= five[i]; --p)
				dp[j][p] = max(dp[j][p], dp[j-1][p-five[i]]+two[i]);
	for(register int i = 6200; i >= 1; --i){
		ans = max(ans, min(i, dp[k][i]));
	}
	cout<<ans;	
	return 0;
}

练习可以做「SCOI2005」互不侵犯

Part 5.树形DP

典型例题P1352 没有上司的舞会

题意：

某大学有 \(n\) 个职员，编号为 \(1 \sim N\)。他们之间有从属关系，也就是说他们的关系就像一棵以校长为根的树，父结点就是子结点的直接上司。现在有个周年庆宴会，宴会每邀请来一个职员都会增加一定的快乐指数 \(a_i\)，但是呢，如果某个职员的直接上司来参加舞会了，那么这个职员就无论如何也不肯来参加舞会了。所以，请你编程计算，邀请哪些职员可以使快乐指数最大，求最大的快乐指数。

解法：

我们设\(dp[i][0]\)为在\(i\)的子树内，不选\(i\)获得的最大快乐值。\(dp[i][1]\)为在\(i\)的子树内，选\(i\)获得的最大快乐值。

首先，这种讨论方法是不重不漏的，最后的答案是所有\(DP\)状态的最大值。

现在考虑如何转移。随便拿一个子树：

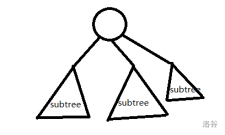
如果该子树的根节点i不选，它的所有子树的根节点自然随便选不选，对于每个它的子树根节点\(j\),\(dp[i][0]+=max(dp[j][0],dp[j][1])\)。

如果该节点选呢。那显然它所有子树的根节点只能不选，\(dp[i][1]+=dp[j][0]\)

这就是最朴素的树形\(DP\)

#include<bits/stdc++.h>
using namespace std;
int n,a,b,ans,dp[9000][2];
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    scanf("%d",&dp[i][1]);
    ans=dp[1][1];
    for(int i=1;i<n;i++){
        scanf("%d%d",&a,&b);
        dp[b][1]+=dp[a][0]; 
        dp[b][0]+=max(dp[a][0],dp[a][1]);
        ans=max(ans,dp[b][1]);
        ans=max(ans,dp[b][0]);
    }
    printf("%d",ans);
}