洛谷-P9455 题解

写在前面：本题蒟蒻给出两种做法，一种乱搞贪心（只是目前能过，若能被 Hack 请和我说），一种正解二分。

---

正文 1

最坏时间复杂度：\(\mathcal{O}(n+\log V)(V=10^9)\)

这个做法是很简单的，在此不多讲。只需要二分超频电压 mid 即可，若当前 mid 可行，则令右边界缩小至 mid，否则令左边界扩大至 mid。

接下来是重要的 check() 函数的编写，请注意塔台之间传输的路线不限，比如塔台 1 可以直接和塔台 \(n\) 通讯。也就是说对于每个塔台 \(i\)，我们首先要确认它向右的通讯范围是目前最大的。

代码：

#include<iostream>
using namespace std;
const int N=5e5+7;
int n,a[N],b[N];
bool check(int x){//判定当前超频电压x的值是否可行
  int t=a[1]+b[1]+x;//起始位
  for(int i=2;i<=n;i++)
    if(t>=a[i])//若该塔台可以覆盖下一个塔台
      t=max(t,a[i]+b[i]+x);//求出更远的可以覆盖到的距离
    else return 0;//否则不可行
  return 1;
}
int main(){
  ios::sync_with_stdio(false),cin.tie(0);
  cin>>n;
  for(int i=1;i<=n;i++) cin>>a[i]>>b[i];
  long long l=0,r=1e9+1,mid;
  while(l<r){//二分
    mid=(l+r)>>1;
    if(check(mid)) r=mid;
    else l=mid+1;
  }
  cout<<l;
}

二分 AC 记录。

正文 2

最坏时间复杂度：\(\mathcal{O}(n)\)

设答案为 \(x\)。

我们简化一下正文 1 的思路，当塔台 \(i\) 的范围被前一个炮台 \(i-1\) 的范围覆盖，即 \(a_{i-1}+b_{1-1}+x\geq a_i+b_i+x\)，我们可以忽略塔台 \(i\) 的范围，直接用塔台 \(i-1\) 的参数贪心即可。

if(a[i]+b[i]+ans>=a[i+1]+b[i+1]+ans)
  {a[i+1]=a[i],b[i+1]=b[i]; continue;}

接下来是贪心，对于每个塔台 \(i\)，只需考虑它能否覆盖到 \(i+1\) 即可，若 \(i\) 无法覆盖 \(i+1\)，则增加超频至可以覆盖到。即：若 \(a_i+b_i+x<a_{i+1}\)，\(x=a_{i+1}-a_i-b_i\)。

if(a[i]+b[i]+ans>=a[i+1]) continue;
ans=max(ans,a[i+1]-a[i]-b[i]);

当然，贪心要有正确性证明。本贪心的思路就是若塔台 \(i-1\) 能到达的最右范围比 \(i\) 远，则忽略 \(i\)，且对于每个 \(i\)，若 \(i\) 无法通讯 \(i+1\)，则增加超频（本段纯属废话）。

证明：

设超频 \(ans\)。

若 \(i-1\) 范围大于 \(i\)，则 \(i-1\) 到 \(i+1\) 所需要增加的 \(ans\) 一定不多于 \(i\) 到 \(i+1\)，因此对于所有 \(i\)，若其范围被 \(i-1\) 覆盖，则将其扔掉（忽略）。

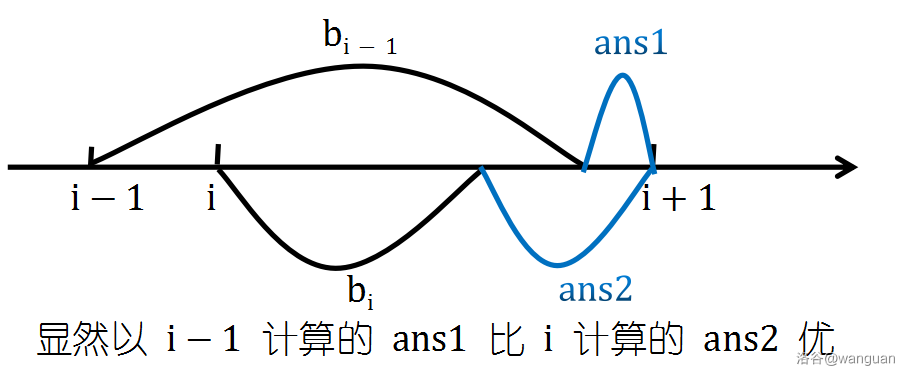
对于每个 \(i\)， \(i+2\) 到 \(i\) 的距离比 \(i+1\) 到 \(i\) 更远，因此 \(i\) 到 \(i+1\) 所需 \(ans\) 比到 \(i+2\) 少。\(i\) 到 \(i+2\) 有两种方式，即传输路线是否有 \(i+1\)。

因为存在前提：\(i+1\) 所能到达的最右距离比 \(i\) 远（不然 \(i+1\) 会被扔掉），所以在相同的 \(ans\) 情况下，经过 \(i+1\) 能到更远，距离 \(i+2\) 更近，所需增加的 \(ans\) 更少。于是对于所有 \(i\)，只需计算 \(i\) 到 \(i+1\) 所需的 \(ans\) 即可，因为这样最优。

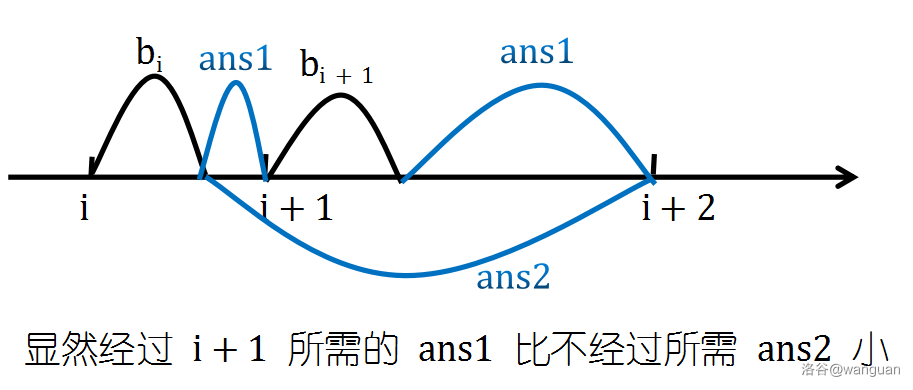
综合一下一个乱搞的贪心就出来了。

代码：

#include<iostream>
using namespace std;
const int N=5e5+7;
int n,ans,a[N],b[N];
int main(){
  ios::sync_with_stdio(false),cin.tie(0);
  cin>>n;
  for(int i=1;i<=n;i++) cin>>a[i]>>b[i];
  for(int i=1;i<n;i++){
    if(a[i]+b[i]+ans>=a[i+1]+b[i+1]+ans)
      {a[i+1]=a[i],b[i+1]=b[i]; continue;}
    if(a[i]+b[i]+ans>=a[i+1]) continue;
    ans=max(ans,a[i+1]-a[i]-b[i]);
  }
  cout<<ans;
}

贪心 AC 记录，可以看到贪心快了 0.17 秒。

后附

日志

v1.1 on 2023.07.17: 改进详细