模拟退火算法

模拟退火算法是求解最优化问题的一种手段。

一种随机算法，相当于爬山，我们总是往高处爬，即使下一步的位置低于现在的位置，考虑到局部最优解的存在，我们也以一定概率接受它。

step1：先设定好初始温度t0=最高温度tMax, 随机选定一个初始状态i，计算f(i)；
step2：若在当前温度下达到内层循环的退出条件，则转step3执行；否则，从邻域N(i)中随机选择一个状态j, 并计算出exp((f(i) - f(j))/temperature)，
若exp((f(i) - f(j))/temperature)>random(0, 1), 则重复执行step2;
step3: 若温度t满足退出条件，则转step2执行；

/*
* J(y)：在状态y时的评价函数值
* Y(i)：表示当前状态
* Y(i+1)：表示新的状态
* r： 用于控制降温的快慢
* T： 系统的温度，系统初始应该要处于一个高温的状态
* T_min ：温度的下限，若温度T达到T_min，则停止搜索
*/
while( T > T_min )
{
　　dE = J( Y(i+1) ) - J( Y(i) ) ; 

　　if ( dE >=0 ) //表达移动后得到更优解，则总是接受移动
       Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
　　else
　　{
       // 函数exp( dE/T )的取值范围是(0,1) ，dE/T越大，则exp( dE/T )也
       if ( exp( dE/T ) > random( 0 , 1 ) )
           Y(i+1) = Y(i) ; //接受从Y(i)到Y(i+1)的移动
　　}
　　    T = r * T ; //降温退火 ，0<r<1 。r越大，降温越慢；r越小，降温越快
　　/*
　　* 若r过大，则搜索到全局最优解的可能会较高，但搜索的过程也就较长。若r过小，则搜索的过程会很快，但最终可能会达到一个局部最优值
　　*/
　　i ++ ;
}

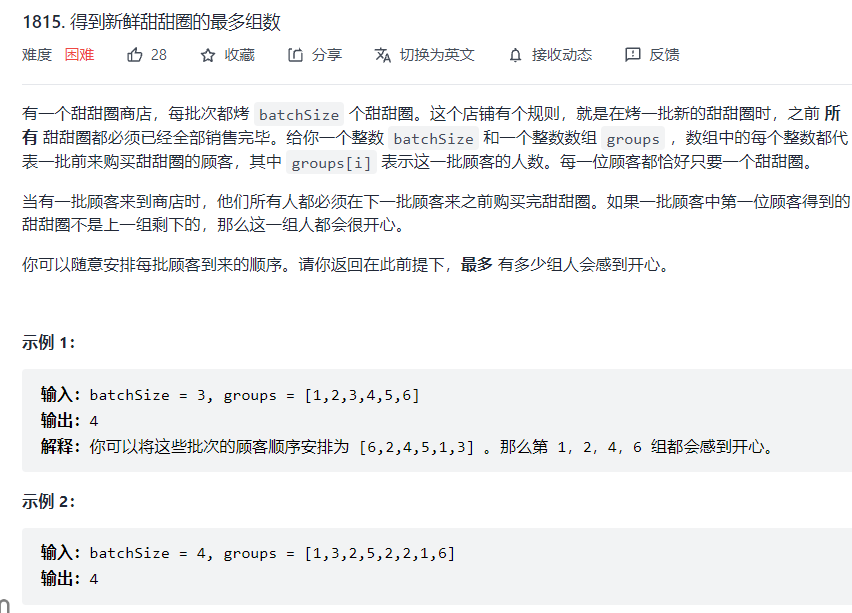
看一道例题：

class Solution {
    int m;
    Random random;
    int max=0;
    public int maxHappyGroups(int batchSize, int[] groups) {
        if(batchSize==1){
            return groups.length;
        }
         m=batchSize;
         random=new Random();
         for(int i=0;i<50;i++){
             backfire(groups);
         }

         return max;
    }
    //计算当前排列的高兴的组数
    public int value(int[] w){
                int n = w.length;
        int res = 0;
        for (int i = 0, s = 0; i < n; i++) {
            if (s == 0) res++;
            if (w[i]>s){
                s= (w[i]-s)%m ==0? 0:m-(w[i]-s)%m; 
            }else{
                s=s-w[i];
            }
        }

        max=Math.max(res,max);
        return res;

    }

    public void backfire(int[] groups){
        double r=0.97;
        int n=groups.length;

        for(double t=1e6;t>1e-6;t=t*r){
            int value1=value(groups);
            //随机交换位置
            int a = random.nextInt(n);
            int b = random.nextInt(n);
            if (a == b) b = (b + 1) % n;
            swap(groups,a,b);
            int value2=value(groups);

            int d=value2-value1;
            if(d>0){
                continue;
            }
            if(Math.exp(d/t)>Math.random()) continue;
            swap(groups,a,b);
            
        }
        

    }
    
    //交换数组中的两个元素的位置
    public void swap(int[] groups,int i,int j){
        int temp=groups[i];
        groups[i]=groups[j];
        groups[j]=temp;
    }
}