三数之和

三数之和

题目

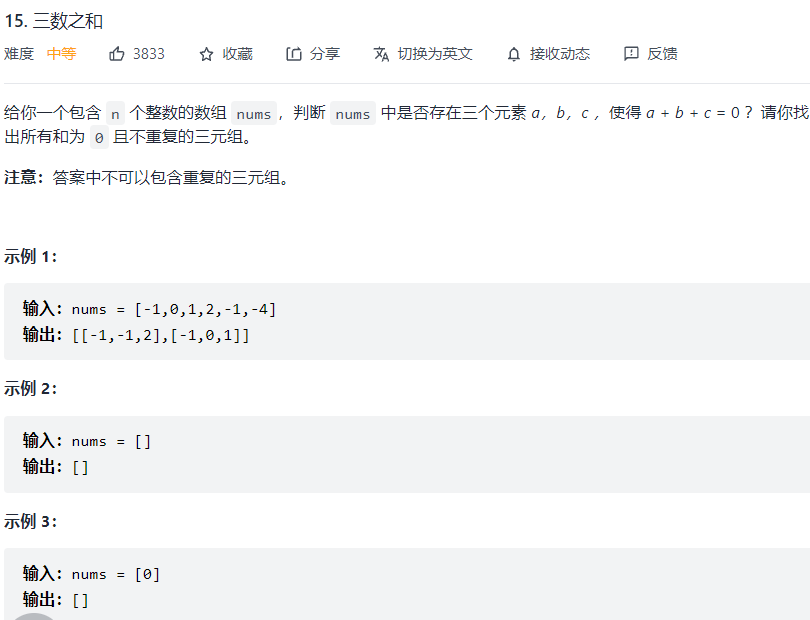
分析

第一种

三数之和我们的思路是先排序，然后枚举第一个数，然后用双指针去找另外两个数

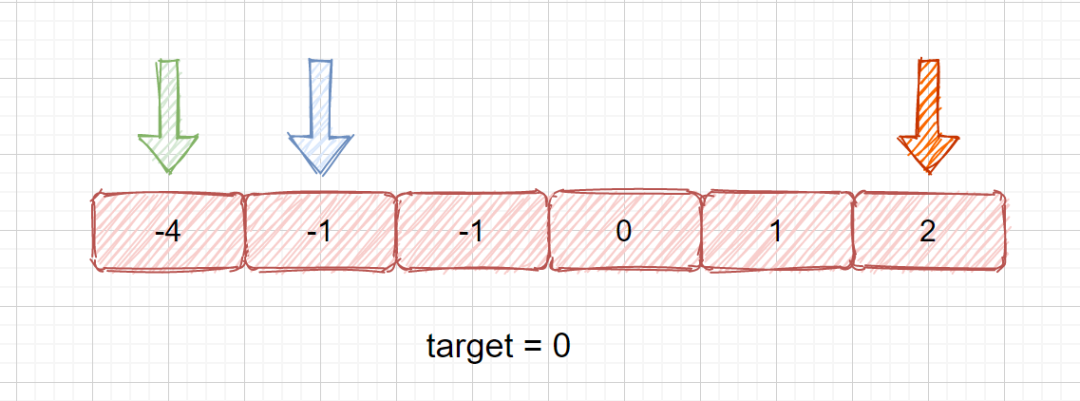
考虑此时和为-3<0，在我们固定住第一个数(绿色指针)的情况下，可以增大第二个数（蓝色指针），如果三数之和大于0，那么我们就缩小第三个数（橙色）。

需要注意的是我们如何排除重复的组合，当我们发现当前指针指向的和刚才指向的数相等时，就跳过

class Solution {
    public List<List<Integer>> threeSum(int[] nums) {
        int n = nums.length;
        Arrays.sort(nums);
        List<List<Integer>> ans = new ArrayList<List<Integer>>();
        // 枚举 第一个数
        for (int first = 0; first < n; first++) {
            // 需要和上一次枚举的数不相同
            if (first > 0 && nums[first] == nums[first - 1]) {
                continue;
            }
            int second=first+1;
            int third=nums.length-1;
            //枚举第二个 第三个数
            while(second<third){
                int sum=nums[first]+nums[second]+nums[third];
                if(sum==0){
                    ans.add(new ArrayList<>(Arrays.asList(nums[first],nums[second],nums[third])));
                    //判断下一个数是否和当前这个数相等，相等则跳过
                    while(second<third &&nums[second]==nums[second+1]){
                        second++;
                    }
                    while(second<third && nums[third]==nums[third-1]){
                         third--;
                    }
                    second++;
                    third--;
                }else if(sum>0){
                    third--;
                }else{
                    second++;
                }
             }
          }
        return ans;
    }   
}

复杂度为O（N^2）

第二种

第二种思路是枚举前两个数，最后一个数用Hash表找，整体复杂度还是O（N^2）,只不过消耗了O（N）的空间

四数之和

题目

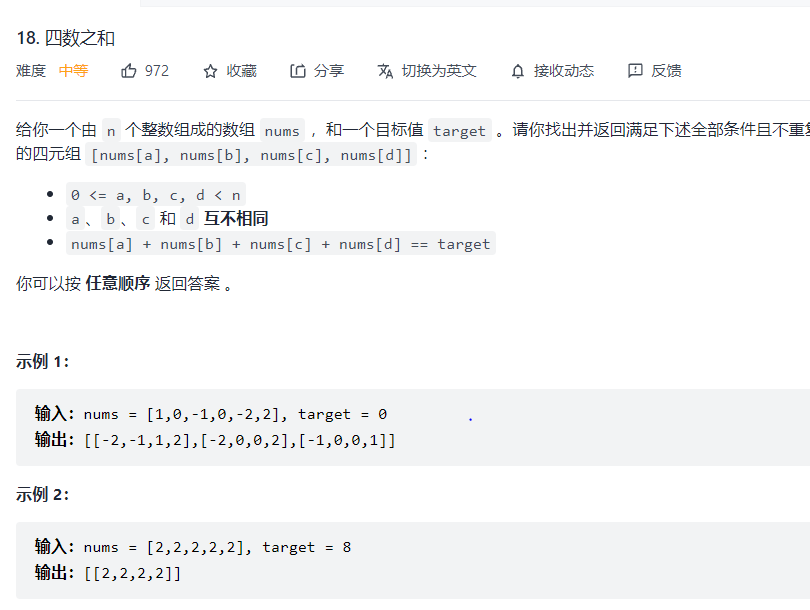
分析

跟三数之和思路相同，这次我们枚举前两个数，用双指针枚举后两个数

class Solution {
    public List<List<Integer>> fourSum(int[] nums, int target) {
        int n=nums.length;
        Arrays.sort(nums);
        List<List<Integer>> res=new ArrayList<>();
        for(int i=0;i<n;i++){
            //遇到重复就跳过
            if(i>0 && nums[i]==nums[i-1]){
                continue;
            }
            for(int j=i+1;j<n;j++){
                 if(j>i+1 && nums[j]==nums[j-1]){
                     continue;
                 }
                 int tar=target-nums[i]-nums[j];
                 int l=j+1;
                 int r=n-1;
                 while(l<r){
                     int sum=nums[l]+nums[r];
                     if(sum==tar){
                         res.add(new ArrayList(Arrays.asList(nums[i],nums[j],nums[l],nums[r])));
                          while(l<r && nums[l] ==nums[l+1])  l++;
                          while(l<r && nums[r] == nums[r-1]) r--;
                          l++;
                           r--;
                     }else if(sum>tar){
                         r--;
                     }else{
                         l++;
                     }
                    
                 }
            }
        }
        return res;

    }
}