dp背包问题

背包问题本质

背包问题是「动态规划」中十分经典的一类问题，背包问题本质上属于组合优化的「 完全问题」。

如果你不了解什么是「 完全问题」，没有关系，丝毫不影响你求解背包问题。

你可以将「 完全问题」简单理解为「无法直接求解」的问题。

例如「分解质因数」问题，我们无法像四则运算（加减乘除）那样，按照特定的逻辑进行求解。

只能通过「穷举」+「验证」的方式进行求解。

既然本质上是一个无法避免「穷举」的问题，自然会联想到「动态规划」，事实上背包问题也同时满足「无后效性」的要求。

这就是为什么「背包问题」会使用「动态规划」来求解的根本原因。

如果按照常见的「背包问题」的题型来抽象模型的话，「背包问题」大概是对应这样的一类问题：

泛指一类「给定价值与成本」，同时「限定决策规则」，在这样的条件下，如何实现价值最大化的问题。

01背包问题

「01背包」是指给定物品价值与体积（对应了「给定价值与成本」），在规定容量下（对应了「限定决策规则」）如何使得所选物品的总价值最大。

题目描述

有 N 件物品和一个容量是 V 的背包。每件物品有且只有一件。

第 i 件物品的体积是 v[i] ，价值是 w[i] 。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

示例 1：

输入: N = 3, V = 4, v = [4,2,3], w = [4,2,3]
输出: 4
解释: 只选第一件物品，可使价值最大。
示例 2：

输入: N = 3, V = 5, v = [4,2,3], w = [4,2,3]
输出: 5
解释: 不选第一件物品，选择第二件和第三件物品，可使价值最大。

dp[N][C+1] 解法

「状态转移方程」为

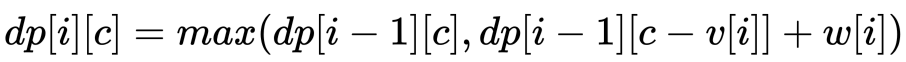
一个二维数组，其中一维代表当前「当前枚举到哪件物品」，另外一维「现在的剩余容量」，数组装的是「最大价值」。

根据 dp 数组不难得出状态定义：

考虑前 i 件物品，使用容量不超过 c 的条件下的背包最大价值。

当有了状态定义之后，我们再根据「最后一步」选择来推导「状态转移方程」。

不失一般性的，我们只需要考虑第 i 件物品如何选择即可，对于第 i 件物品，我们有「选」和「不选」两种决策。

结合我们的「状态定义」，「不选」方案的「最大价值」很好确定：

「不选」其实就是 ，等效于我们只考虑前 i-1 件物品，当前容量为 c 的情况下的最大价值。

同理，如果我们选第 i 件物品的话，代表消耗了 v[i] 的背包容量，获取了 w[i] 的价值，那么留给前 i-1 件物品的背包容量就只剩 c-v[i] 。即最大价值为dp[i-1][c-v[i]]+w[i] 。

当然，选第 件有一个前提：「当前剩余的背包容量」>=「物品的体积」。

在「选」和「不选」之间取最大值，就是我们「考虑前 i 件物品，使用容量不超过 C 」的条件下的「背包最大价值」。

class Solution {
    public int maxValue(int N, int C, int[] v, int[] w) {
        int[][] dp = new int[N][C+1];
        // 先处理「考虑第一件物品」的情况
        for (int i = 0; i <= C; i++) {
            dp[0][i] = i >= v[0] ? w[0] : 0;
        }
        // 再处理「考虑其余物品」的情况
        for (int i = 1; i < N; i++) {
            for (int j = 0; j < C + 1; j++) {
                // 不选该物品
                int n = dp[i-1][j]; 
                // 选择该物品，前提「剩余容量」大于等于「物品体积」
                int y = j >= v[i] ? dp[i-1][j-v[i]] + w[i] : 0; 
                dp[i][j] = Math.max(n, y);
            }
        }
        return dp[N-1][C];
    }
}

dp[2][C+1] 解法

根据「转移方程」，我们知道计算第 行格子只需要第 行中的某些值。

也就是计算「某一行」的时候只需要依赖「前一行」。

因此可以用一个只有两行的数组来存储中间结果，根据当前计算的行号是偶数还是奇数来交替使用第 0 行和第 1 行。

这样的空间优化方法称为「滚动数组」

这种空间优化方法十分推荐，因为改动起来没有任何思维难度。

只需要将代表行的维度修改成 2，并将所有使用行维度的地方从 i 改成 i%2 或者 i&1 即可（更建议使用 i&1 ，& 运算在不同 CPU 架构的机器上要比 % 运算稳定）。

class Solution {
    public int maxValue(int N, int C, int[] v, int[] w) {
        int[][] dp = new int[2][C+1];
        // 先处理「考虑第一件物品」的情况
        for (int i = 0; i < C + 1; i++) {
            dp[0][i] = i >= v[0] ? w[0] : 0;
        }
        // 再处理「考虑其余物品」的情况
        for (int i = 1; i < N; i++) {
            for (int j = 0; j < C + 1; j++) {
                // 不选该物品
                int n = dp[(i-1)&1][j]; 
                // 选择该物品
                int y = j >= v[i] ? dp[(i-1)&1][j-v[i]] + w[i] : 0;
                dp[i&1][j] = Math.max(n, y);
            }
        }
        return dp[(N-1)&1][C];
    }
}

dp[C+1] 解法

事实上，我们还能继续进行空间优化，只保留代表「剩余容量」的维度。

再次观察我们的「转移方程」：

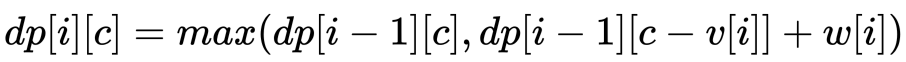
不难发现当求解第 i 行格子的值时，不仅是只依赖第 i-1 行，还明确只依赖第 i-1 行的第 c 个格子和第 c-v[i] 个格子（也就是对应着第 i 个物品不选和选的两种情况）。

换句话说，只依赖于「上一个格子的位置」以及「上一个格子的左边位置」。

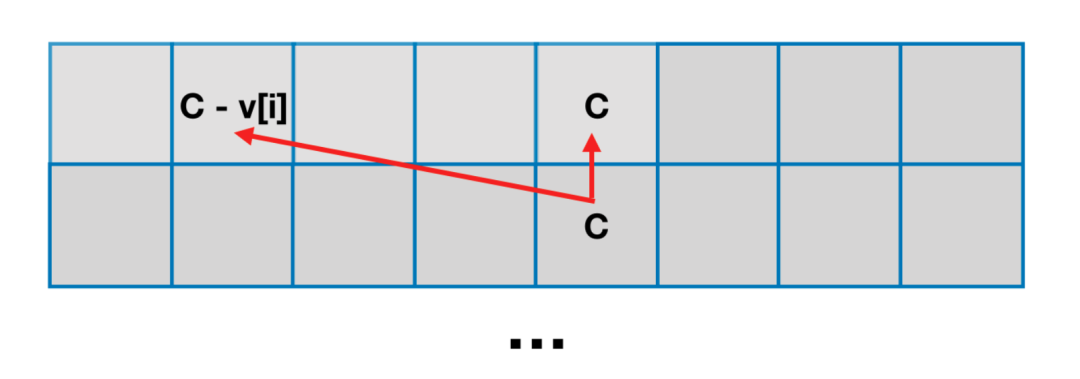
因此，只要我们将求解第 i 行格子的顺序「从 0 到 C 」改为「从 C 到 0 」，就可以将原本 2 行的二维数组压缩到一行（转换为一维数组）。

这样做的空间复杂度和「滚动数组」优化的空间复杂度是一样的。但仍然具有意义，而且这样的「一维空间」优化，是求解其他背包问题的基础，需要重点掌握。

实质就是不断更新掉上一行第c个格子 和 第c-v[i] 个 格子

class Solution {
    public int maxValue(int N, int C, int[] v, int[] w) {
        int[] dp = new int[C + 1];
        for (int i = 0; i < N; i++) {
            for (int j = C; j >= v[i]; j--) {
                // 不选该物品
                int n = dp[j]; 
                // 选择该物品
                int y = dp[j-v[i]] + w[i]; 
                dp[j] = Math.max(n, y);
            }
        }
        return dp[C];
    }
}

题目

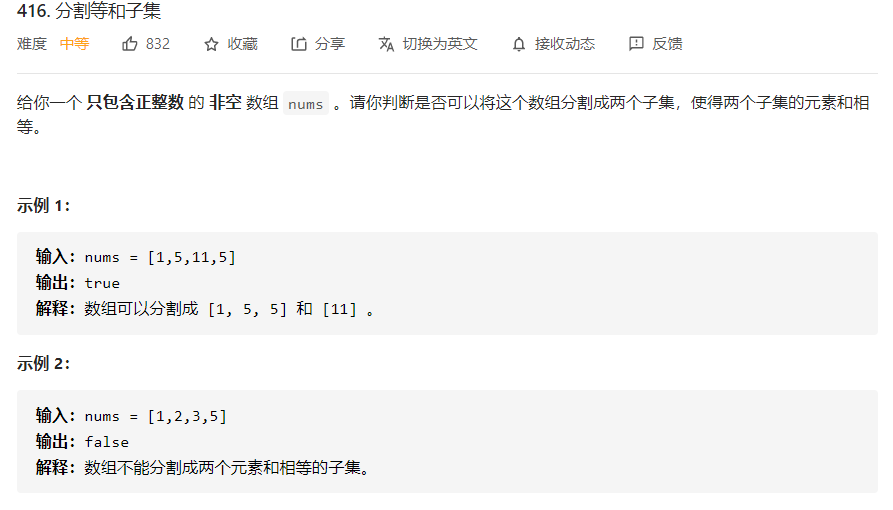
通常「背包问题」相关的题，都是在考察我们的「建模」能力，也就是将问题转换为「背包问题」的能力。

由于本题是问我们能否将一个数组分成两个「等和」子集。

问题等效于「能否从数组中挑选若干个元素，使得元素总和等于所有元素总和的一半」。

这道题如果抽象成「背包问题」的话，应该是：

我们背包容量为sum/2 ，每个数组元素的「价值」与「成本」都是其数值大小，求我们能否装满背包。

因此不难得出状态转移方程：

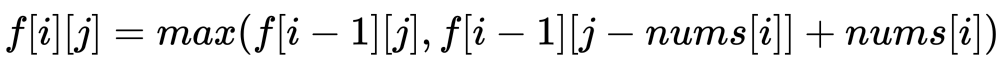
class Solution {
    public boolean canPartition(int[] nums) {
        int n = nums.length;

        //「等和子集」的和必然是总和的一半
        int sum = 0;
        for (int i : nums) sum += i;
        int target = sum / 2;
        
        // 对应了总和为奇数的情况，注定不能被分为两个「等和子集」
        if (target * 2 != sum) return false;

        int[][] f = new int[n][target + 1];
        // 先处理考虑第 1 件物品的情况
        for (int j = 0; j <= target; j++) {
            f[0][j] = j >= nums[0] ? nums[0] : 0;
        }

        // 再处理考虑其余物品的情况
        for (int i = 1; i < n; i++) {
            int t = nums[i];
            for (int j = 0; j <= target; j++) {
                // 不选第 i 件物品
                int no = f[i-1][j];
                // 选第 i 件物品
                int yes = j >= t ? f[i-1][j-t] + t : 0;
                f[i][j] = Math.max(no, yes);
            }
        }
        // 如果最大价值等于 target，说明可以拆分成两个「等和子集」
        return f[n-1][target] == target;
    }
}

这里再给出一维空间解法：

class Solution {
    public boolean canPartition(int[] nums) {
        int n = nums.length;

        //「等和子集」的和必然是总和的一半
        int sum = 0;
        for (int i : nums) sum += i;
        int target = sum / 2;

        // 对应了总和为奇数的情况，注定不能被分为两个「等和子集」
        if (target * 2 != sum) return false;

        // 将「物品维度」取消
        int[] f = new int[target + 1];
        for (int i = 0; i < n; i++) {
            int t = nums[i];
            // 将「容量维度」改成从大到小遍历
            for (int j = target; j >= 0; j--) {
                // 不选第 i 件物品
                int no = f[j];
                // 选第 i 件物品
                int yes = j >= t ? f[j-t] + t : 0;
                f[j] = Math.max(no, yes);
            }
        }
        // 如果最大价值等于 target，说明可以拆分成两个「等和子集」
        return f[target] == target;
    }
}

完全背包问题

有 N 种物品和一个容量为 C 的背包，每种物品都有无限件。

第 i 件物品的体积是 v[i] ，价值是 w[i] 。

求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

其实就是在 0-1 背包问题的基础上，增加了每件物品可以选择多次的特点（在容量允许的情况下）。

示例 1：

输入: N = 2, C = 5, v = [1,2], w = [1,2]
输出: 5
解释: 选一件物品 1，再选两件物品 2，可使价值最大。

我们可以直接将 01 背包的「状态定义」拿过来用：

dp[i][j] 代表考虑前 i 件物品，放入一个容量为 j 的背包可以获得的最大价值。

由于每件物品可以被选择多次，因此对于某个 dp[i][j] 而言，其值应该为以下所有可能方案中的最大值：

选择 0 件物品 i 的最大价值，即 dp[i-1][j]

选择 1 件物品 i 的最大价值，即 dp[i-1][j-v[i]]+w[i]

选择 2 件物品 i 的最大价值，即 dp[i-1][j-2v[i]]+2w[i]

...

选择 k 件物品 i 的最大价值，dp[i-1][j-kv[i]]+kw[i]

由此我们可以得出「状态转移方程」为：

class Solution {
    public int maxValue(int N, int C, int[] v, int[] w) {
        int[][] dp = new int[N][C + 1];
        
        // 先预处理第一件物品
        for (int j = 0; j <= C; j++) {
            // 显然当只有一件物品的时候，在容量允许的情况下，能选多少件就选多少件
            int maxK = j / v[0];
            dp[0][j] = maxK * w[0];
        }
        
        // 处理剩余物品
        for (int i = 1; i < N; i++) {
            for (int j = 0; j <= C; j++) {
                // 不考虑第 i 件物品的情况（选择 0 件物品 i）
                int n = dp[i - 1][j];
                // 考虑第 i 件物品的情况
                int y = 0;
                for (int k = 1 ;; k++) {
                    if (j < v[i] * k) {
                        break;
                    }
                    y = Math.max(y, dp[i - 1][j - k * v[i]] + k * w[i]);
                }
                dp[i][j] = Math.max(n, y);
            }
        }
        return dp[N - 1][C];
    }
}

滚动数组解法

class Solution {
    public int maxValue(int N, int C, int[] v, int[] w) {
        int[][] dp = new int[2][C + 1];
        
        // 先预处理第一件物品
        for (int j = 0; j <= C; j++) {
            // 显然当我们只有一件物品的时候，在容量允许的情况下，能选多少件就选多少件
            int maxK = j / v[0];
            dp[0][j] = maxK * w[0];
        }
        
        // 处理剩余物品
        for (int i = 1; i < N; i++) {
            for (int j = 0; j <= C; j++) {
                // 不考虑第 i 件物品的情况（选择 0 件物品 i）
                int n = dp[(i - 1)&1][j];
                // 考虑第 i 件物品的情况
                int y = 0;
                for (int k = 1 ;; k++) {
                    if (j < v[i] * k) {
                        break;
                    }
                    y = Math.max(y, dp[(i - 1)&1][j - k * v[i]] + k * w[i]);
                }
                dp[i&1][j] = Math.max(n, y);
            }
        }
        return dp[(N - 1)&1][C];
    }
}

一维空间解法

我们知道在 01 背包中，最重要的是「一维空间优化」解法。

之所以 01 背包能够使用「一维空间优化」解法，是因为当我们开始处理第 i 件物品的时候，数组中存储的是已经处理完的第 i-1 件物品的状态值。

然后配合着我们容量维度「从大到小」的遍历顺序，可以确保我们在更新某个状态时，所需要用到的状态值不会被覆盖。

因此 01 背包问题的状态转移方程为：

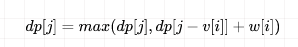
同时容量维度的遍历顺序为从大到小。

而「完全背包」区别于「01 背包」，在于每件物品可以被选择多次。

我们来看下dp[i][j]与dp[i][j-v[i]]的关系

因此完全背包问题状态转移方程也可以表示为

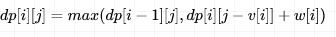
由于计算 dp[i][j] 的时候，依赖于dp[i][j-v[i]] 。

因此我们在改为「一维空间优化」时，需要确保 dp[j-v[i]] 存储的是当前行的值，即确保 dp[j-v[i]] 已经被更新，所以遍历方向是从小到大。

class Solution {
    public int maxValue(int N, int C, int[] v, int[] w) {
        int[] dp = new int[C + 1];
        for (int i = 0; i < N; i++) {
            for (int j = 0; j <= C; j++) {
                // 不考虑第 i 件物品的情况（选择 0 件物品 i）
                int n = dp[j];
                // 考虑第 i 件物品的情况
                int y = j - v[i] >= 0 ? dp[j - v[i]] + w[i] : 0; 
                dp[j] = Math.max(n, y);
            }
        }
        return dp[C];
    }
}

题目

完全平方数

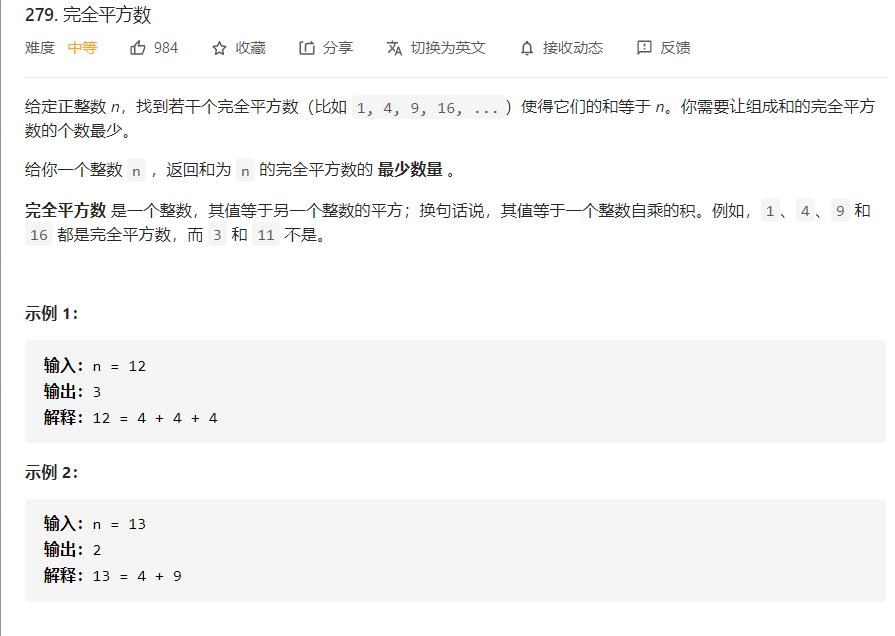
可以看到从有限个数中选出若干个，使得和为给定的值，这是一个完全背包问题。

一维空间解法

class Solution {
    public int numSquares(int n) {
        int[] f = new int[n + 1];
        //初始化 填充最大值
        Arrays.fill(f, 0x3f3f3f3f);
        f[0] = 0;
        for (int t = 1; t * t <= n; t++) {
            int x = t * t;
            for (int j = x; j <= n; j++) {
                f[j] = Math.min(f[j], f[j - x] + 1);
            }
        }
        return f[n];
    }
}

零钱兑换

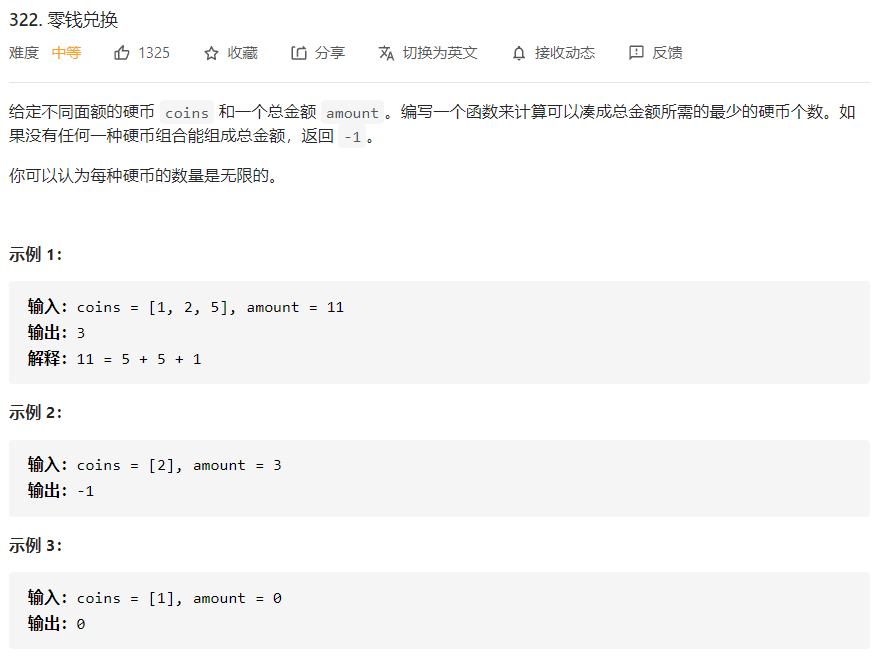
一维空间解法

class Solution {
    public int coinChange(int[] coins, int amount) {
        int[] dp=new int[amount+1];
        Arrays.fill(dp,Integer.MAX_VALUE);
        dp[0]=0;
        for(int i=0;i<coins.length;i++){
            for(int j=0;j<=amount;j++){
                if(j-coins[i]<0){
                    continue;
                }
                //这里要防止Integer.MAX_VALUE+1后溢出
                dp[j]=Math.min(dp[j],dp[j-coins[i]]==Integer.MAX_VALUE ? Integer.MAX_VALUE : dp[j-coins[i]]+1);
            }
        }
        return dp[amount]==Integer.MAX_VALUE ? -1:dp[amount];

    
    }
}

零钱兑换II

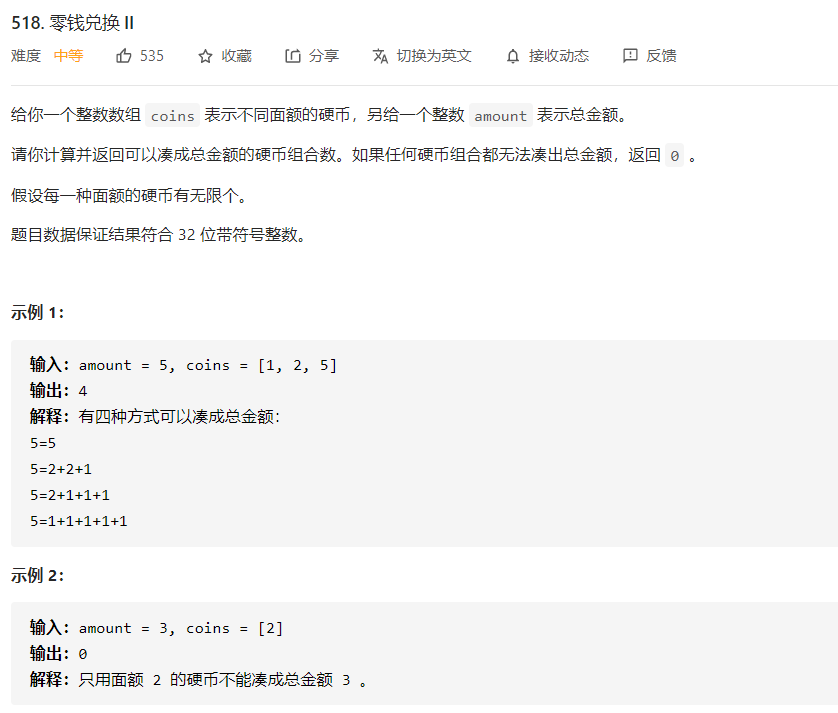
一维空间解法

class Solution {
    public int change(int cnt, int[] cs) {
        int n = cs.length;
        int[] f = new int[cnt + 1];
        f[0] = 1;
        for (int i = 1; i <= n; i++) {
            int val = cs[i - 1];
            for (int j = val; j <= cnt; j++) {
                f[j] =f[j]+ f[j - val];
            }
        }
        return f[cnt];
    }
}