二分查找 模板+经典例题

模板

左加右不加

long l = 0, r = 1000009;
//注意是<不带等于号
while (l < r) {
    long mid = l + r + 1 >> 1; //如果是l=mid的话，需要加1，加1是防止死循环
    if (check(mid)) {
        l = mid; //这里l可以使mid
    } else {
        r = mid - 1;
    }
}
return l;


long l = 0, r = 1000009;
while (l < r) {
    long mid = l + r >> 1;//r=mid不加1
    if (check(mid)) {
        r = mid;//这里r可以使mid
    } else {
        l = mid + 1;
    }
}
return r;

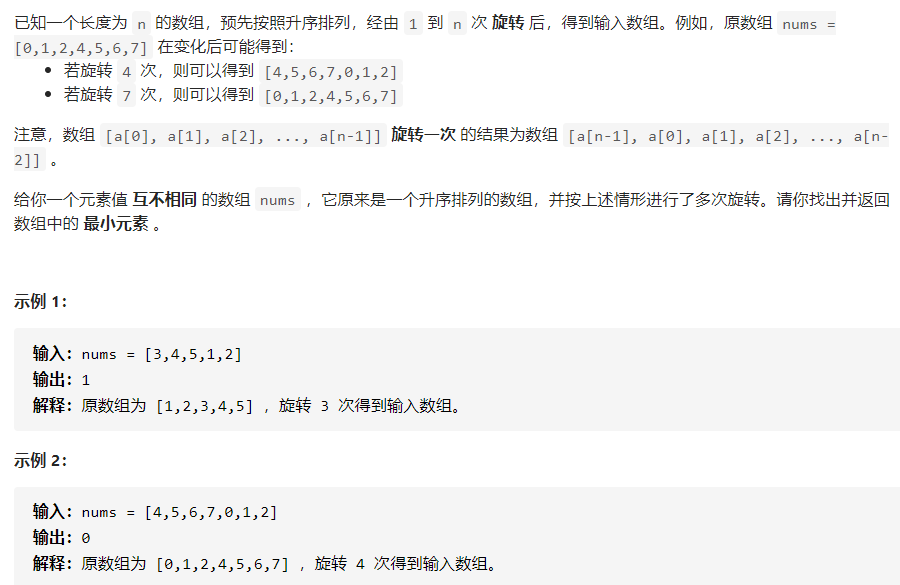
题目：寻找旋转排序数组的最小值

解法

二分查找的本质是具有两段性

做了旋转后

  *
*
        *
      *
    *

我们以nums[0]为界，可以分为>=nums[0]的一段和小于nums[0]的一段，现在我们要找最小值，最小值应该在两段的边界

    public int findMin(int[] nums) {
         int left=0;
         int right=nums.length-1;
         int mid=0;

         while(left<right){
        
           mid=left+(right-left)/2;
           //此时mid在左段，因此我们可以收缩左边界
           if(nums[0]<=nums[mid]){
               //这里mid不可能是最小值
               left=mid+1;
           }else{
               //这里right可能是最小值
               right=mid;
           }
         }
        //考虑到可能[1,2,3]这种没有旋转的这时两段的边界值是3但是最小值不是3
         return nums[right]<nums[0]?nums[right]:nums[0];
    }

变种：

如果不能保证数组中的数不重复的话，就不能保证两段性，因此我们要制造两段性

  while(left<right && nums[right]==nums[0]){
             right--;
         }

题目：搜索旋转排序数组

解法：

根据上题的分析，我们可以看出以nums[0]为界具有两段性，我们先找到分割点，再判断target在哪一段

 public int search(int[] nums, int target) {
        int n = nums.length;
        if (n == 0) return -1;
        if (n == 1) return nums[0] == target ? 0 : -1;

        // 第一次「二分」：从中间开始找，找到满足 >=nums[0] 的分割点（旋转点）
        int l = 0, r = n - 1;
        while (l < r) {
            int mid = l + r  >> 1;
            if (nums[mid] >= nums[0]) {
                l = mid+1;
            } else {
                r = mid ;
            }
        }

        // 第二次「二分」：通过和 nums[0] 进行比较，得知 target 是在旋转点的左边还是右边
        if (target >= nums[0]) {
            l = 0;
        } else {
            l = l + 1;
            r = n - 1;
        }
        while (l < r) {
            int mid = l + r >> 1;
            if (nums[mid] >= target) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }

        return nums[r] == target ? r : -1;
    }

题目：在排序数组中查找元素的第一个位置和最后一个位置

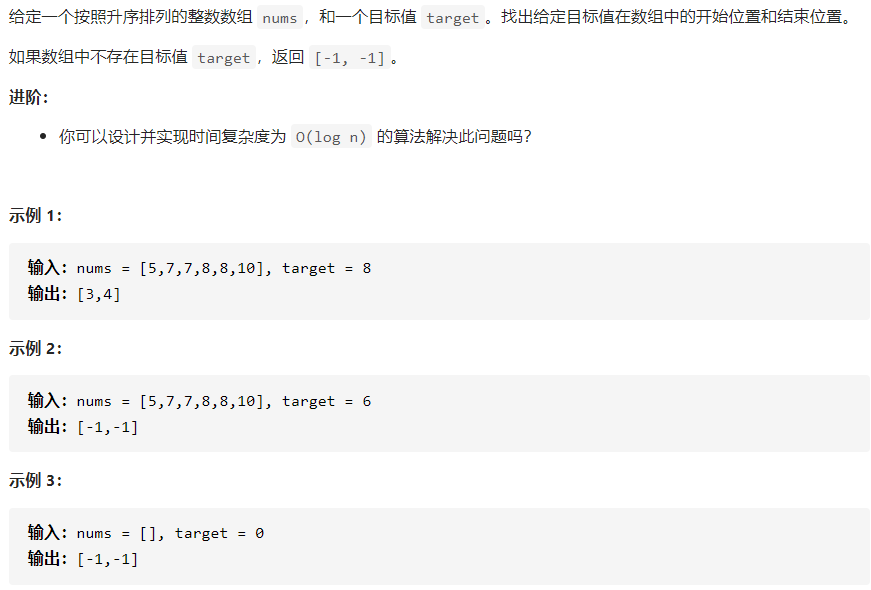
解法：

//两次二分，第一次找出最左边等于target的下标（nums[mid]=target时 让right=mid即可），第二次找出最右边的下边
class Solution {
    public int[] searchRange(int[] nums, int target) {
        int[] ans = new int[]{-1, -1};
        int n = nums.length;
        if (n == 0) return ans;

        int l = 0, r = n - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (nums[mid] >= target) {
                r = mid;
            } else {
                l = mid + 1;
            }
        }
        if (nums[l] != target) {
            return ans;
        } else {
            ans[0] = l;
            l = 0; r = n - 1;
            while (l < r) {
                int mid = l + r + 1 >> 1;
                if (nums[mid] <= target) {
                    l = mid;
                } else {
                    r = mid - 1;
                }
            } 
            ans[1] = l;
            return ans;
        }
    }
}

题目：在 D 天内送达包裹的能力

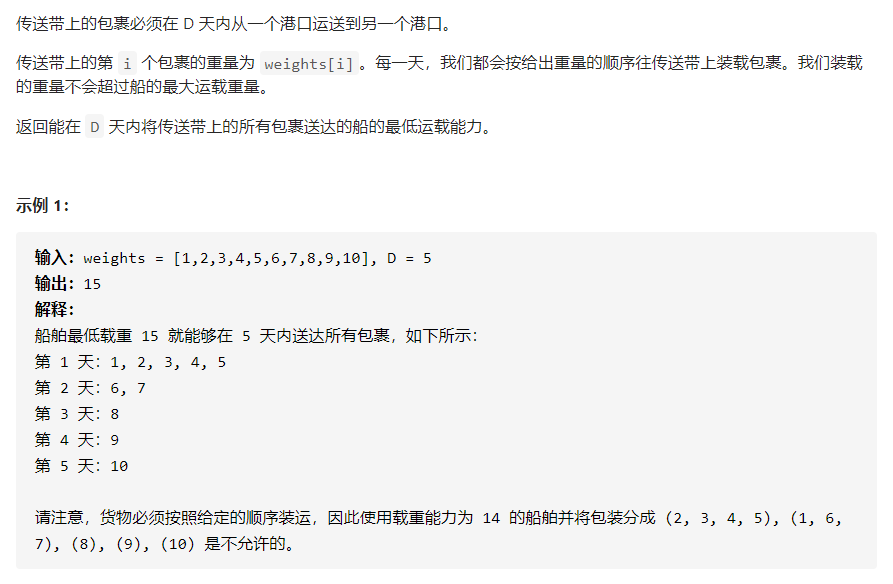
解法：

很明显存在一个边界，载重大于边界能在D天内送完，小于边界不能在D天内送完，于是具有“二分特性”，我们找到边界即可

class Solution {
    public int shipWithinDays(int[] weights, int D) {
        int l=0;
        int r=0;
        for(int weight:weights){
           r+=weight;
        }
        int mid=0;
        while(l<r){
           mid=(r+l)>>1;
           if(check(weights,D,mid)){
               //r=mid能一直找到最小的符合条件的边界
               r=mid;
           }else{
               l=mid+1;
           }
        }
        return r;

    }
    public boolean check(int[] weights,int D,int mid){
        int sum=0;
        int day=1;
        for(int i=0;i<weights.length;i++){   
           //某个物品的大小超过了运输能力
            if(weights[i]>mid){
                return  false;
            }
         //当天运不下就放下一天运
             if(sum+weights[i]>mid){
                 sum=0;
                 day++;
             }
             sum+=weights[i];
        }
         //有可能最后一天超过了运输能力
          if(sum>mid){
                return  false;
            }
        if(day<=D){
            return true;
        }else{
            return false;
        }
    }
}