【排序】

选择排序：
选择排序的基本思想是：如果有N个元素需要排序，那么首先从N个元素中找到最小的那个元素与第0位置上的元素交换（说明一点，如果没有比原本在第0位置上的元素小的就不用交换了，后面的同样是），然后再从剩下的N-1个元素中找到最小的元素与第1位置上的元素交换，之后再从剩下的N-2个元素中找到最小的元素与第2位置上的元素交换，直到所有元素都排序好（也就是直到从剩下的2个元素中找到最小的元素与第N-2位置上的元素交换）。
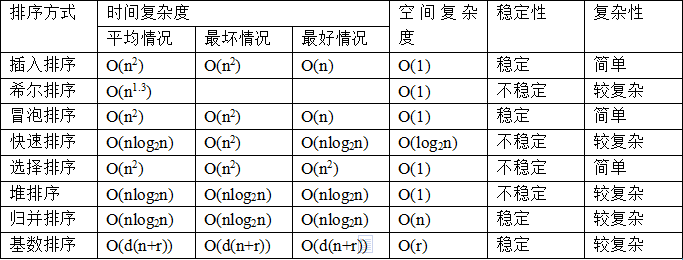
时间复杂度：最好、最坏、平均 都是 O(N^2)

def select_sort(nums):
    for i in range(len(nums)):
        for j in range(i, len(nums)):
            if nums[j] < nums[i]:
                nums[j], nums[i] = nums[i], nums[j]
    return nums

冒泡排序：
冒泡排序需要两两元素进行比较，如果是升序排序，每一轮总会把最大的元素放在数组末尾。第一层for循环，leng-1表示需要进行交换的轮数，第二次for循环，j记录了交换两个元素的下标。下边范围每一轮都会减少。因为每次都把这一轮的最大元素放在后面。
平均情况和最坏情况O(N^2)，最好情况，有序的时候不用交换O(N)。

def bubble_sort(nums):
    for i in range(len(nums) - 1, -1, -1):
        for j in range(i):
            if nums[j + 1] < nums[j]:
                nums[j + 1], nums[j] = nums[j], nums[j + 1]
    return nums

快速排序：
空间复杂度：O(n) 因为递归实现需要占用内存
平均时间复杂度：O(nlogn) ，最坏时间复杂度：O(N^2)

def quick_sort(nums, left, right):
    if left < right:
        base = partition(nums, left, right)
        quick_sort(nums, left, base - 1)
        quick_sort(nums, base+1, right)
    return nums


def partition(nums, left, right):
    pivot = nums[left]
    while left < right:
        while left < right and nums[right] >= pivot:
            right -= 1
        nums[left] = nums[right]
        while left < right and nums[left] <= pivot:
            left += 1
        nums[right] = nums[left]
    nums[left] = pivot
    return left

堆排序:
时间复杂度：平均和最坏都是O(nlogn)

def heap_sort(nums):
    build_heap(nums)
    for i in range(len(nums)-1,-1,-1):
        nums[0],nums[i] = nums[i],nums[0]
        heapfy(nums,0,i)
    return nums

def build_heap(nums):
    for i in range((len(nums)-1)//2,-1,-1):
        heapfy(nums,i,len(nums))

def heapfy(nums,i,length):
    left = 2*i+1
    right = 2*i+2
    if left<length and nums[left]>nums[i]:
        large = left
    else:
        large = i
    if right<length and nums[right]>nums[large]:
        large = right
    if i!=large:
        nums[i], nums[large] = nums[large], nums[i]
        heapfy(nums,large,length)

不稳定的排序算法：一堆希尔快选