PID控制
序言
对于一个系统(or模型),无论它是数学系统、机械系统、电路系统等等,我们在给定系统一个输入时总是希望系统能够给予预期输出,这就是控制的概念。对于实体系统,由于系统内部非线性、微分/积分等机理,其实际输出与预期(理想)输出相比往往具有延迟性、不准确、不稳定等缺陷,自动控制理论就是研究如何使得系统的实际输出既快又准还稳。
当系统结构参数未知,或者其控制数学模型过于复杂时,PID控制算法是一种有效的控制策略。PID是一种基于误差的模糊控制方法,不需要知道系统的输入输出模型,只需要依据实际输出与期望输出之间的偏差通过不断调整输入就可以近似输出“期望输出”。想起来上小学打扫卫生值日时常常和小伙伴们将扫把倒过来竖在手指上比谁的时间长,我们并不知道该把手指放在哪个位置以及哪个支点上只是看扫把要往那边倒了手指也向相应方向移动,保证扫把不掉下来,这就是模糊控制的一个直接的例子。(未完待续。。。2021年9月17号 10:20:34)
转眼间这个“未完待续。。。”已经拖了快四个月了,时光不知不觉早已步入了2022年。现在是2022年1月6日09:17:33,我在瓜大由于疫情蜗居在宿舍,室友还在呓语而我正和大萌丫一起听着歌码下这段文字。在这四个月里经历了很多也收获了很多,如今回首,不胜今昔之感。不知道多年以后再看现在的文字,回想现在的人和物,又有怎样的感受呢?谨以此文,送给2021吧。
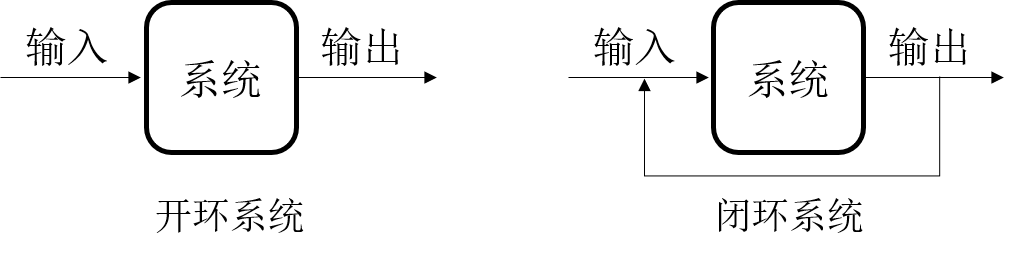
反馈控制系统
反馈控制系统也称为闭环控制系统就是将输出引回输入,当前输出影响(更准确地说是调整)下一时刻的输入,反馈是自动控制的灵魂。
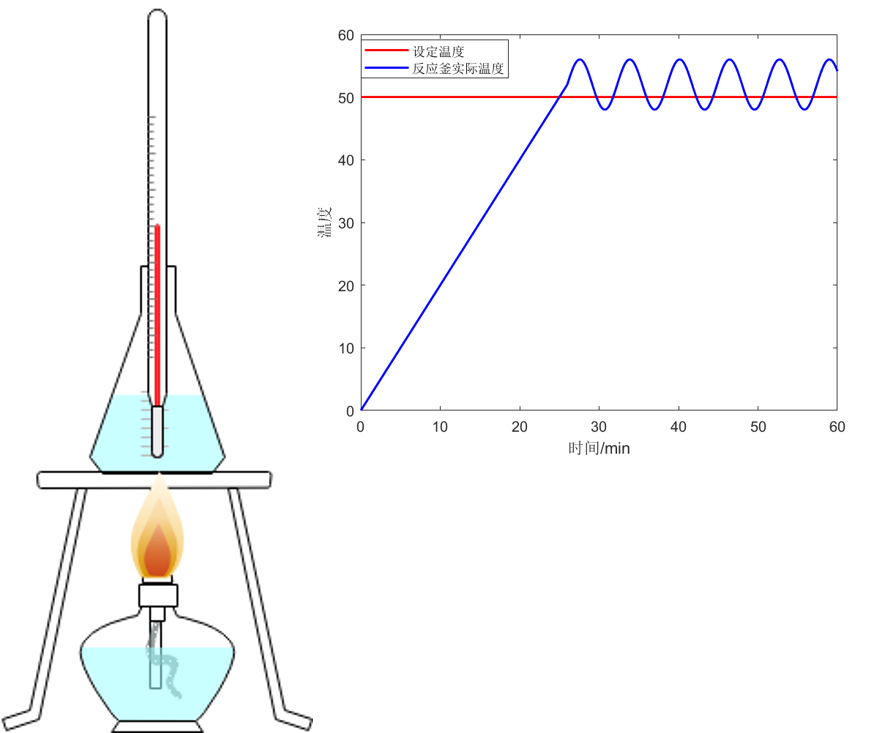
下面以煤气灶烧化学反应釜为例,需要尽可能将釜内温度保持在50度,简单叙述一下对PID在这四个月里的理解。
位式控制

最简单的控制策略就是当釜内水温低于50度时保持煤气灶一直是开着的,一旦水温达到50度就立即关掉煤气灶,当水温低于50度时再次打开煤气灶,如此循环。位式控制有两个缺点:首先只有开关两个动作,只能输出1或0,也就是说它只能控制煤气灶的开或关,却无法调控火的大小,也就是说水温为10和水温为40时火开的大小是一样的,这显然降低了加热效率,我们肯定希望水远低于50度时火开大一点,水温接近50度时火开小一点。其次,水是一个惯性系统(能量不能突变)这会导致,水温50度关闭煤气灶后水温还会继续上升,当水温低于50度打开煤气时水温会下降,也就是说反应釜内的水温实际上是围绕着50度上下波动的。位式控制虽然简单朴素,但理解位式控制及其缺点有助于理解PID控制的来源及本质。
比例控制(P控制)
在位式控制中提到了,位式控制不能调节火的大小,我们想在10度时火开大一点,40度时火开小一点,位式控制都做不到。P控制就是解决这个问题而引入的,其思想就是目标值(50度)减去当前值的误差来控制火开的大小,例如当前温度为10那么与50的误差为40,误差大一点火自然就大一点,当前温度为40那么与50的误差为10,误差小一点火自然就小一点了。具体地,设系统理想输出为\(D\),系统当前输入为\(e=D-d\),将\(D-d\)称为误差,因此\(P\)控制是一种基于误差的控制。
进一步分析P控制,当系统稳定输出时,即:$$d_{t+1}={K_p}*(D-d_t)$$
解得:$$d_{t}= {K_p\over K_p+1}D_p$$
因此P控制是静态有差的,误差 $$\Delta=D-d_t={D\over K_p}$$
由上式可以看出比例控制系数\(K_p\)越大,静态误差\(\Delta\)就越小,最初的温度上升也就越快。那是不是\(K_p\)越大越好呢?当\(K_p\)大了会给系统带来超调和振荡问题。举个简单的例子,设\(K_p\)为100,\(t\)时刻温度为1,则下一时刻\(t+1\)系统的温度为:$$d_{t+1}=K_p*(D-d_t)={100\times(50-1)}=490$$ $$d_{t+2}=K_p (D-d_{t+1})=100\times(50-490)=-4400$$虽然在\(t=\infty\)是系统的静态误差只有\(\Delta=D-d_t={D\over K_p}={50 \div 100}=0.5\),但是在系统稳定之前有超调和振荡问题,因此寄希望于单单通过提高\(K_p\)值来实现快、准、稳是不可行的。
以比例控制算法仿真烧100的化学反应釜,以下各图比例系数\(K_p\)逐渐增大,上升时间缩短但系统超调量增大逐渐失稳。
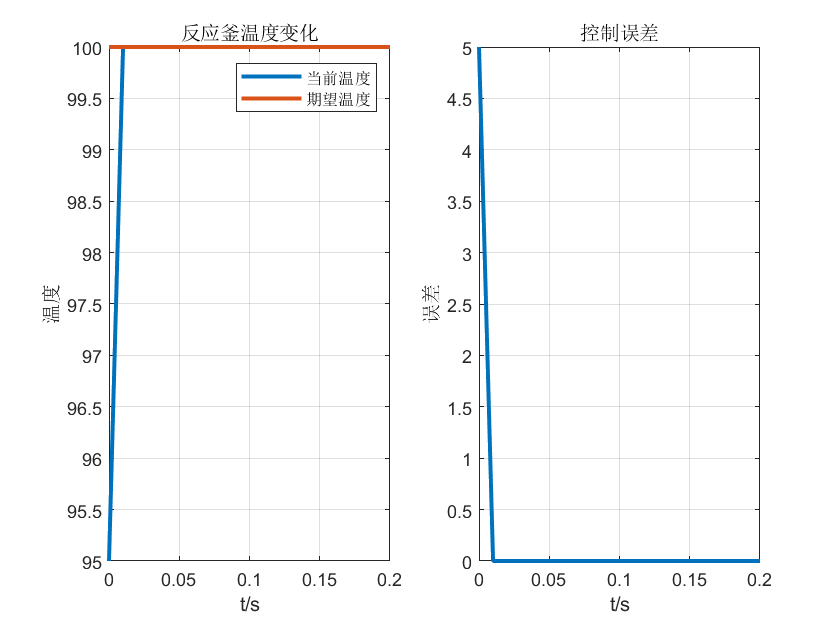
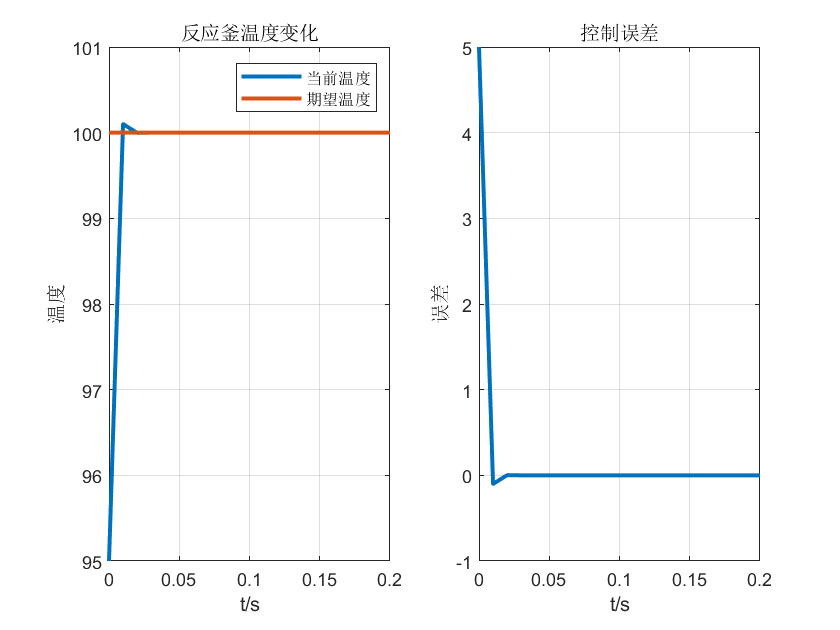
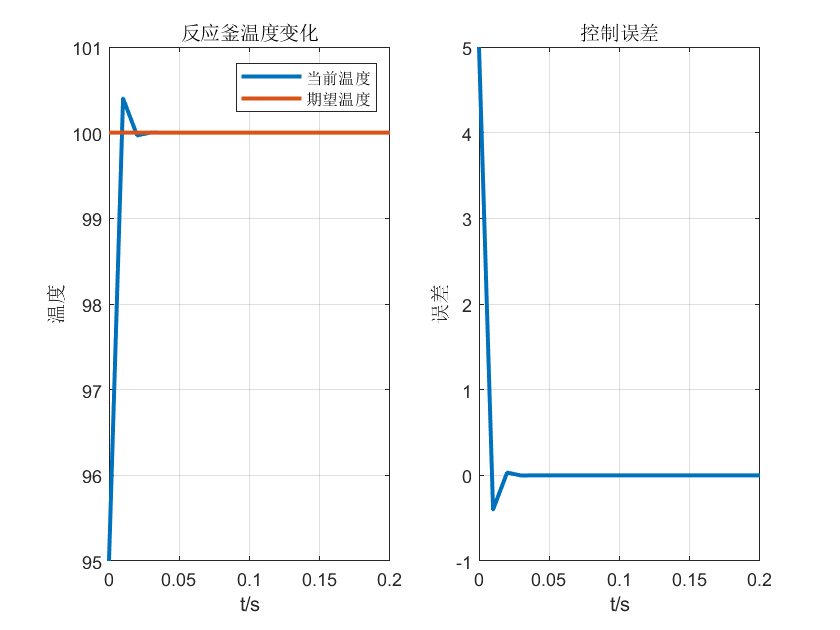
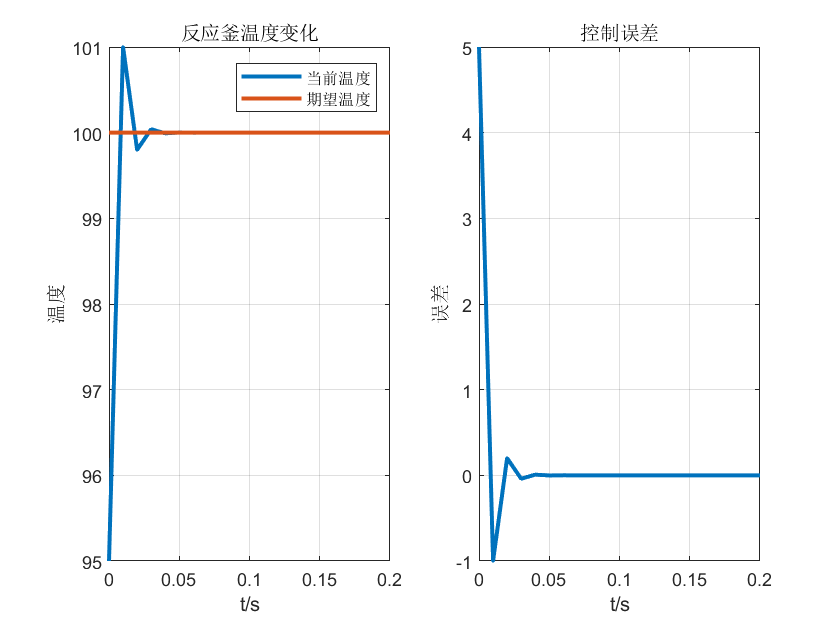
(不知不觉一天有过去了,现在是2022年1月13日23:06:41,现在我又和大萌子听着网易云码下这段文字。语言是思想的边界,一个知识点只有能够讲述给别人听,才算真正掌握。PID回想起来已经学了3年但直到今晚我才算真正部分理解其中的P,这或许就是实践出真知的道理吧。不知道大萌丫此刻又在向着什么又在做些什么,多年以后再看看,回想起疫情的阴霾下两个人分享彼此的歌单,想必会会心一笑吧。既然此篇献给2021,今晚还有时间就简单说说。2021无论从那个方面在我的人生中都留下了浓墨重彩的一笔,本科毕业,步入研究生。今年走过许多地方的桥,看过许多地方的云,也遇见一个最好年华里的她。有别离的惆怅,有相逢的喜悦,有永别的悲伤,有遇见的欣喜,或许这就是人生。不知不觉,我真的感觉到了自己长大了,很多儿时的玩伴回家再遇见时也学会自己曾经讨厌那般虚伪的寒暄。随着年龄的增长,一些人一些事会渐渐逝去,一些人一些事也会渐渐浮起,这就是阅历。一个人儿时可以在母亲的怀抱里恣意撒娇,长大了,就需要独立面对了,还需要用自己的坚强去慰藉、去回馈曾经的所有温暖。不知不觉2022年1月13日23:25:08,I还没说,D还没说,却不得不说未完。。。。)
比例控制公式:$$X_{t+1}=X_{t}+K_{P}*(X_{Desire}-X_{t})$$
点击查看代码
% 比例控制仿真代码
close all;
clear;clc;
kp = 110;
x0 = 95;
xd = 100;
d = 6;
tf = 0.2;
dt = 0.01;
t = 0:dt:tf; %仿真时长段内的关键点
x = zeros(1,length(t)); % 水量数据的存储容器
x(1) = x0;
for i = 2:length(t)
x(i) = x(i-1) + kp*(xd-x(i-1))*dt; %迭代计算
end
figure('Name','水箱容量与误差')
subplot(1,2,1)
plot(t,x,'linewidth',2)
hold on
plot([0,tf],[xd,xd],'linewidth',2)
xlabel('t/s')
ylabel('温度')
grid on
legend('当前温度','期望温度')
title('反应釜温度变化')
subplot(1,2,2)
plot(t,xd-x,'linewidth',2)
xlabel('t/s')
ylabel('误差')
grid on
title('控制误差')
积分控制(I)
(现在是2022年2月1日19:41:24,农历虎年大年初一晚,当旧年的烟火渐渐冷却,当新年的帷幕缓缓拉开,距离上一次码字又过去了将近一个月,想来很是惭愧。因工作产生的劳累短暂休息后就可以缓解,并在休息时感到愉悦,因碌碌无为产生的劳累,在休息时却只有无尽的悔恨与懊恼和空虚。百川东到海,何时复西归,韶光易逝,千金难买寸光阴,回想过去的一年因为经历了很多“大事”,因此这一年很充实、很有意义。一日之计在于晨,一年之计在于春,奋斗吧!)
为了消除比例控制的静态误差,进一步提出积分控制:$$\(E_{t}=\int^{T=t}_{T=0}{X_{Desire}-X(T)dT}\)$
- \(E_{t}>0\)表示过去的多半时间里,输出量未达标
- \(E_{t}=0\)表示过去的时间里,输出量刚好达标
- \(E_{t}<0\)表示过去的多半时间里,输出量已超调
单独的比例控制,当\(t=\infty\)时,输出量始终存在静态误差\(X_{t=\infty}<X_{Desire}\),即\(E_{t}>0\),因此可以把\(E_{t}\)加在\(X_{t=\infty}\)上以消除静态误差。
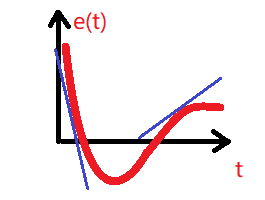
误差曲线图
微分控制
定义:$$\alpha=\frac{\partial D_{t}}{\partial t}$$ 如误差曲线图所示,\(\alpha\)代表误差曲线的切线,反映了误差的变化趋势:
- \(\alpha>0\)表示误差增大
- \(\alpha=0\)表示误差稳定
- \(\alpha<0\)表示误差
离散系统位置式PID公式
PID调参
欲知详情移步自动控制原理
现在是2022年2月1日23:10:57,农历正月初一,这篇拖了几个月的随笔终于告一段落,正如标题所说欲知详情,还需要好好重温自控原理。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号