什么是树（Tree）

只有一个根节点，每个父节点下有一个或多个子节点，每个子节点之间(兄弟节点)不相连

 

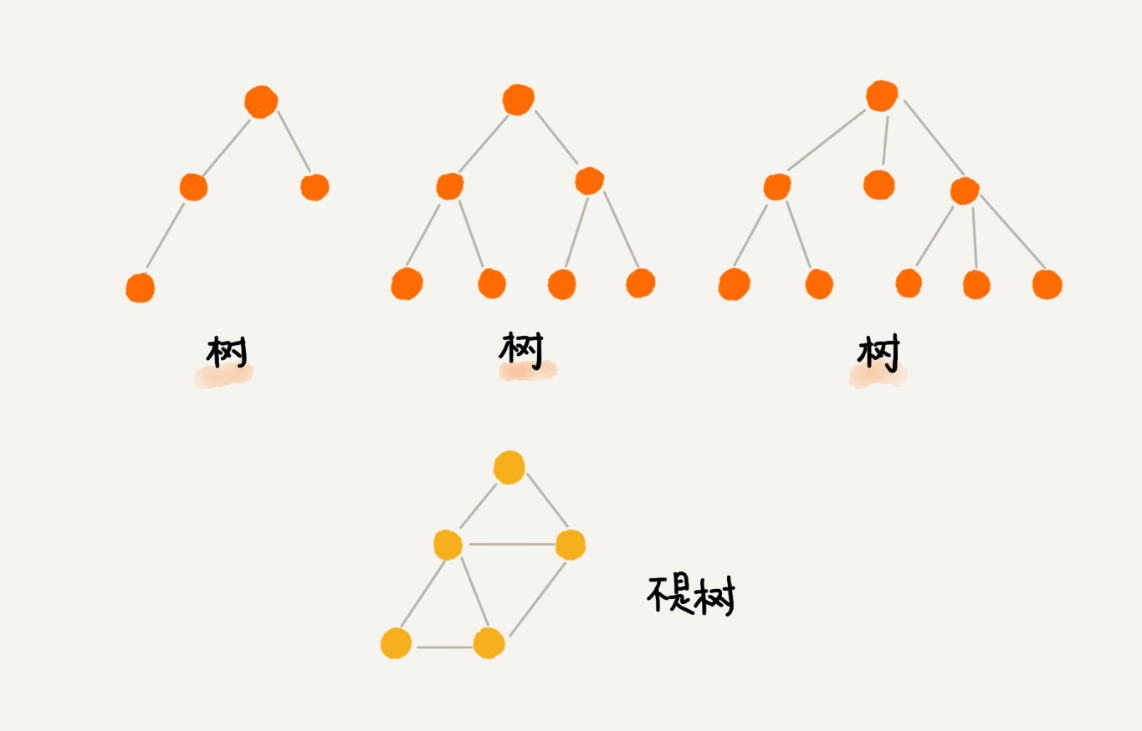
 关于树， 有三个概念：

高度（height）

节点的高度 = 节点到叶子节点的最长路径（边数）

数的高度 = 根节点的高度

深度（depth）

节点的深度 = 根节点到这个节点所经历的边的个数

层（level）

节点的层数 = 节点的深度 + 1

 

 

高度是从下往上度量，计数起点是0

深度是从上往下度量，计数起点是0

层数也是从上往下度量，计数起始点为1，也就是根节点的层数是1

 

二叉树

二叉树的每个节点最多有两个子节点，分别是左子节点和右子节点。

满二叉树 除了叶子节点，每个节点都有两个子节点

完全二叉树 最后一层子节点靠左排列的叫做完全二叉树，（要么左子节点和右子节点都有，要么只有左子节点并且左子节点后没有叶子节点了）

 

 如何存储二叉树

二叉树有两种存方法。

 

 

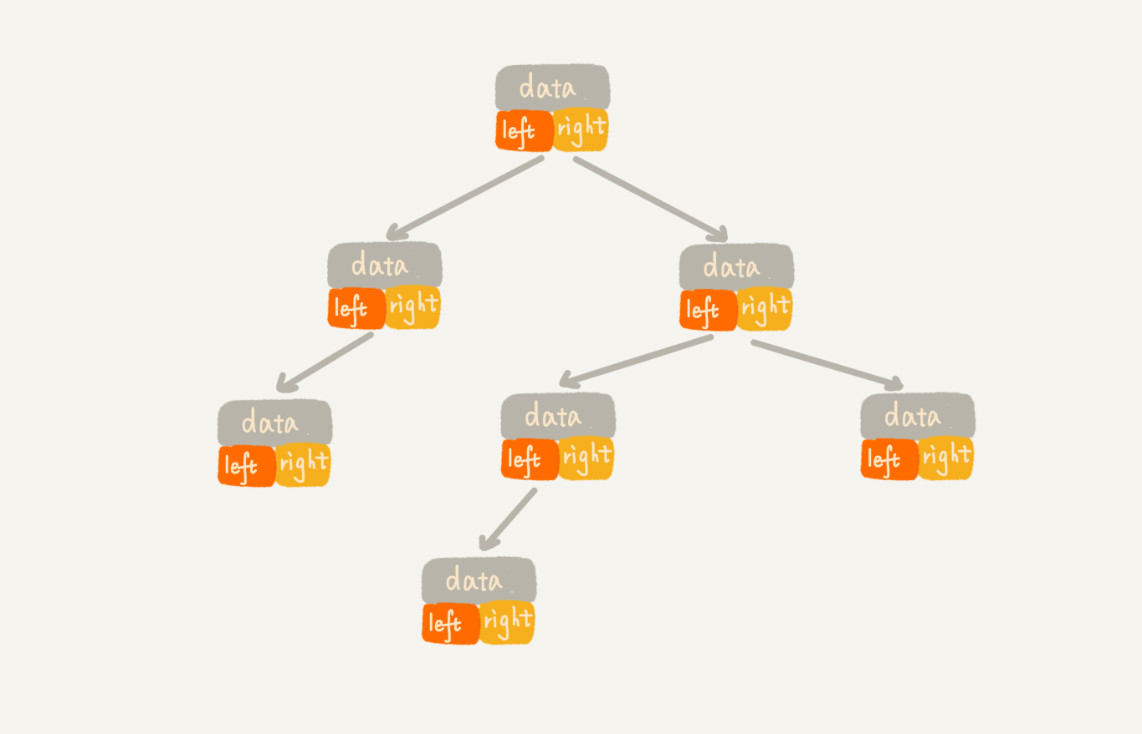
 基于指针或引用的的二叉链式存储⬆️

每个节点有三个字段，分别保存节点数据和左右子节点的地址，只要得到根节点，就可以通过左右子节点的指针把整棵树串联起来

 

 

 

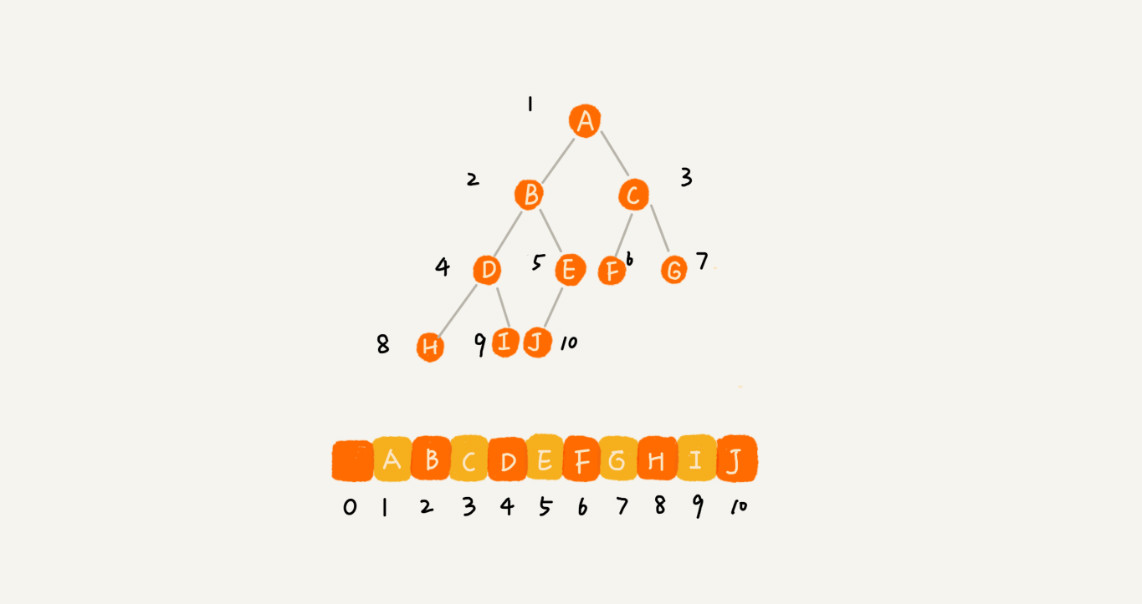
 基于数组的顺序存储⬆️

把根节点存储在下标i=1的位置上，左子节点存储在2*i=2的位置，右子节点在2*i+1的位置。以此类推

也就是父节点 = i 左子节点 = i*2 右子节点 = i *2 +1

完全二叉树是最省空间的一种二叉树，用数组存储只浪费一个头结点0

 

二叉树的遍历

前序遍历： 对于节点A，先打印A->再打印A的左子树->再打印A的右子树

中序遍历：对于节点A，先打印节点A的左子树->再打印A->再打印A的右子树

后续遍历：对于节点A，先打印节点A的左子树->再打印A的右子树->再打印A

也就是说，A节点在什么位置（前中后）它就是什么顺序

实际上，前中后续遍历二叉树就是一个递归的过程

class TraversalBinaryTree:
    """
    前中后续遍历二叉树
    :return:
    """
    def __init__(self, tree):
        """
        tree 是以数组存储的二叉树
        """
        self.tree = tree

    def pre_order(self, n_index):
        """
        n: int 需要遍历的节点位置
        前序遍历
        :return:
        """
        if n_index < 0 or n_index > len(self.tree):
            print "over"
            return
        print self.tree[n_index]
        print self.pre_order(n_index*2)
        print self.pre_order(n_index*2 + 1)

    def in_order(self, n_index):
        """
        中序遍历
        :param n_index:
        :return:
        """
        if n_index < 0 or n_index > len(self.tree):
            print "over"
            return
        print self.in_order(n_index*2)
        print self.tree[n_index]
        print self.in_order(n_index*2 + 1)

    def post_order(self, n_index):
        """
        后序遍历
        :param n_index:
        :return:
        """
        if n_index < 0 or n_index > len(self.tree):
            print "over"
            return
        print self.post_order(n_index*2)
        print self.post_order(n_index*2 + 1)
        print self.post_order(n_index)