线性回归问题的几种解决思路

线性回归问题是用于研究因变量（目标变量）与一个或多个自变量（特征变量）之间的线性关系。一个基础的线性回归问题：在最基础的线性回归问题中，给定一组数据点 (x,y)，目标是求解线性方程$$y=ax+b$$中系数a和b，使得该直线最能反映数据的内在规律。

最小二乘法

几何思路

我们尝试将数据代入方程中，问题转化成求解线性方程组：

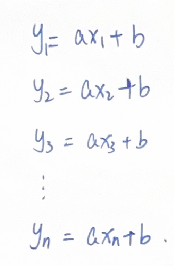
用矩阵表达：

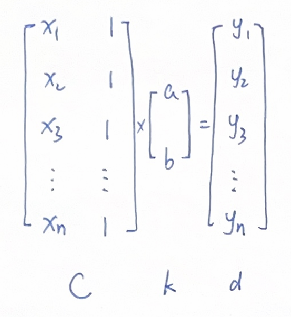
如果方程有解，说明所有数据点都在这条线性关系的直线上，求解这个方程即可。
然而大多数情况下，由于数据点众多，上图中矩阵C的列向量空间（列向量的所有线性组合）是高维空间（n维）中的一个平面，d很难刚好位于这个平面之上，也就是方程组很难有解。
此时，我们需要找到这样的a，b，使得Ck（也就是预测值）距离d的距离尽可能近，从几何关系描述，就是要求解d在C的列向量空间中的投影（因为投影的距离是最近的）。
通过正交性条件可以推导出正规方程：

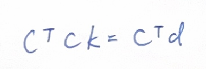
展开得：

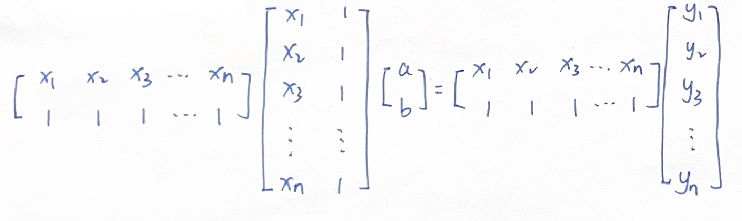
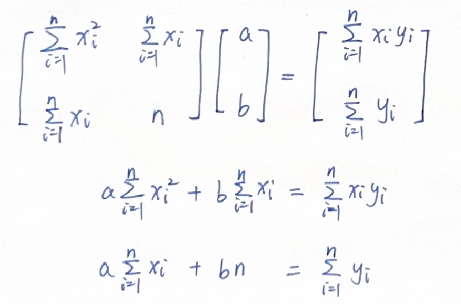
求解可得a，b

微分思路

从微分的角度，我们构建一个预测值和实际值的误差方程E：

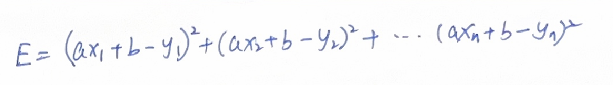
求解a，b使得E最小，也就是令E对a，b的偏导数为0：

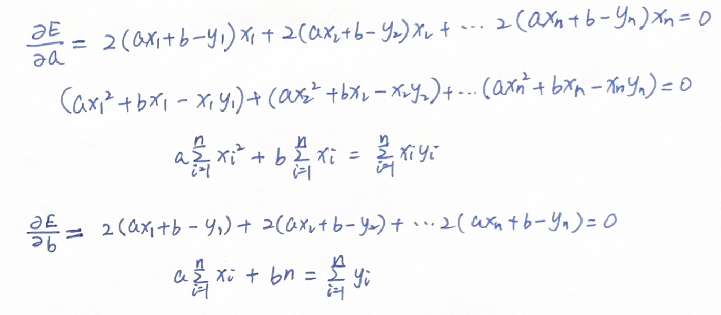
可以看到，这个结果和上面通过几何的方式得到的方程是一样的。

也就是说，向量投影的正交条件与误差平方和的极值条件在数学上是等价的。

梯度下降方法

我们用神经元的图示来表述上述线性关系：

从梯度下降的角度，参数a，b要沿着误差关于他们的梯度方向进行迭代：

这个误差E其实就是梯度下降里的loss function，如果用上文微分方法中的E的计算方式，这相当于用所有数据进行梯度下降，也就是full gradient descent。如果采用单个数据进行每一次迭代，则为随机梯度下降（stochastic gradient descent，SGD） 。

总结

最小二乘法是一种直接求解的思路，适用于数据量较少的场景，能够快速得到解析解。然而，当数据量增加且特征数量增多时，矩阵运算的复杂度会显著上升，导致计算资源消耗过大，求解效率降低。

相比之下，梯度下降方法是一种迭代优化算法，更适合处理大规模数据集和复杂模型（如深度神经网络）。它通过逐步逼近最优解，能够在资源有限的情况下高效地完成优化任务，尤其在面对高维特征和复杂结构时表现出更强的适应性和灵活性。