03 常见激活函数详解
在01 深度学习基础及前向神经网络中,我们在讲解前向传播时,向中间层加入了Relu激活函数。我们提到这是为了向模型中添加非线性特性,从而让模型具有更强的表达能力。本篇将继续研究一些常见的激活函数,以及他们不同的特性。
1. 什么是激活函数
我们看一个基本的神经网络模型:
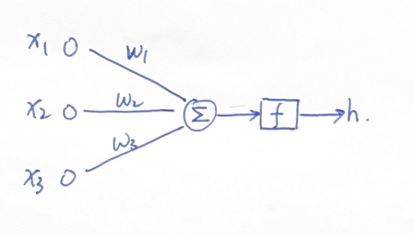
其中输入的x1,x2,x3三个特征通过加权求和,形成一个新的特征,这个新的特征通过一个函数f,将输出h传递到下一层去。这个f就是激活函数。
所以激活函数就是把这个新的特征保留并映射出来,把神经元的输入映射到输出端。
“激活(activation)”这个讲法,可以理解为打开/关闭(比如ReLU函数);也可以理解为映射(如sigmoid、tanh等函数)。
2. 为什么要用激活函数
引入非线性特性
如前文所说,激活函数的主要作用就是为神经网络引入非线性特性,使其能够拟合复杂的函数,捕捉数据中的复杂模式。如果没有激活函数,形如 y=((((xW1)W2)W3)W4) 的纯线性网络模型,无论有多少中间层,都会退化成 y = x(W1W2W3W4) = xW 的单层线性模型,无法逼近复杂函数。
控制梯度传播
由于反向传播遵循链式法则,梯度计算是逐层相乘的关系,当神经网络的层数增加,一些层上的梯度过小或过大,都会让最终计算出的权重更新量不稳定(消失或爆炸)。而一些激活函数的导数特性,能有效地降低这样的影响。
输出范围限定
由于层与层之间是通过加权和进行计算,加权和的结果很可能不可控,我们希望得到可控的、限定在一定范围以内的结果,就需要引入一些能限定输出范围的激活函数。此外,对于输出节点,其取值范围是与任务需求相关联的,也能通过激活函数对其进行限定。
3. 什么样的函数能被用作激活函数
根据上文中激活函数的作用,我们很容易推测出激活函数的以下特性:
- 非线性:这是引入激活函数的主要作用。
- 可微性:以便在反向传播中计算和控制梯度。
- 单调性:在反向传播中,梯度的方向决定了参数更新的方向。如果激活函数是单调的,梯度的符号(正或负)在局部范围内保持一致,这有助于参数朝着正确的方向更新。
- 输出范围:能够将输出限定在一定范围以内的函数。
- 计算效率:由于深度神经网络的存在,激活函数的计算成本应该尽可能低。
4. 常见激活函数
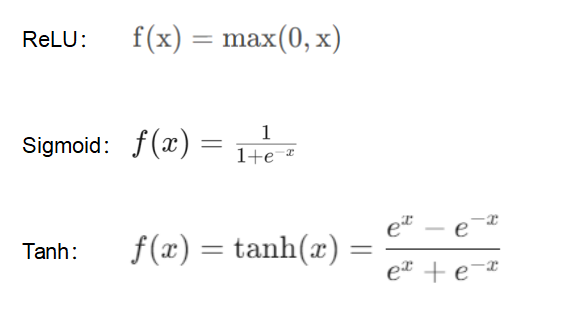
下面,我们从多个角度来横向对比研究这三个激活函数。
4.1 函数输出
三个函数的图像如下图:
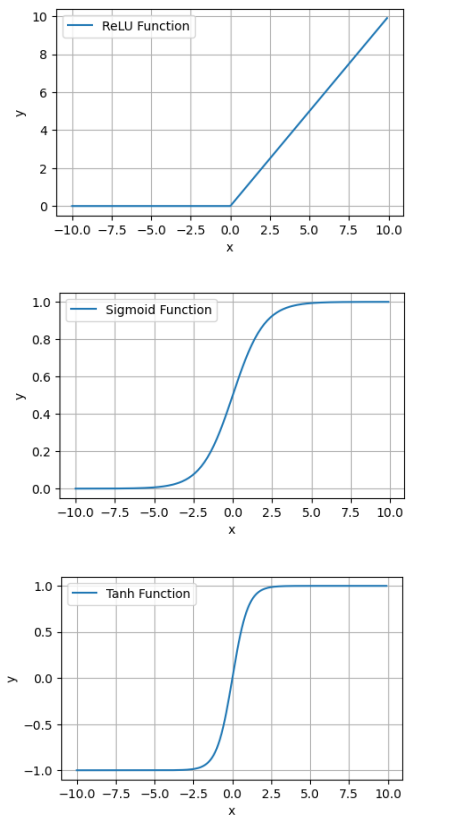
ReLU函数最能体现激活函数中”激活“二字的含义,当进行加权求和后进入神经元节点的数值为正值,则保留其输出,该节点处于”激活状态“;当输入神经元节点的数值为负值,则令其输出为0,该节点处于关闭状态。
这也是复合仿生学原理的:大脑相关研究表明生物神经元讯息编码通常比较分散和稀疏。通常情况下大脑中在同一时间大概只有1%-4%的神经元处于激活状态。
Sigmoid函数的输出范围为(0, 1),在二分类问题中,输出类别只有两种,”是“或”否“,比如图片中有没有猫(有vs没有),这类问题的输出通常我们采用一个0-1的值进行表示,该数值可以体现结果为”是“的概率。因此Sigmoid函数的输出特性适合处理这类概率问题。
Tanh函数的输出范围为(-1, 1),相比Sigmoid的(0, 1),Tanh的输出以零为中心,这有助于加速网络的收敛,缓解梯度下降中的震荡问题,加快收敛速度。
为什么激活函数的输出会影响收敛速度
从上一篇讨论反向传播的文章中可以发现,当计算参数矩阵W的梯度时,最后一个要乘的梯度是前一层神经元的输出,也就是激活函数的输出。
我们聚焦在神经网络中的其中两层,如图:
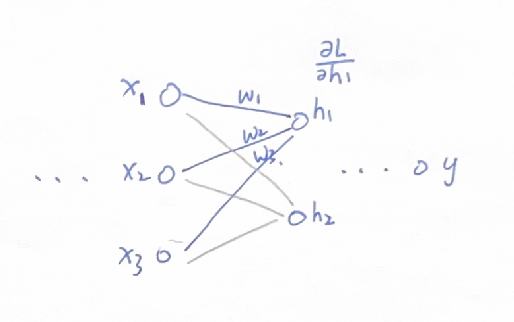
其中,对于神经元h1来说,其对应前一层的权重分别为w1,w2,w3,其梯度可以写成:
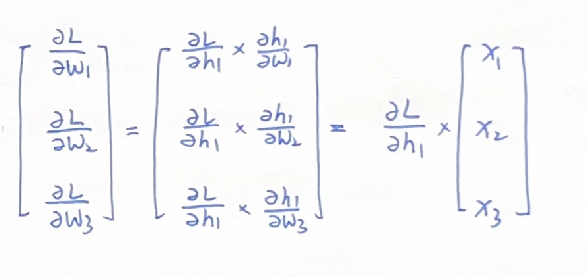
此时,如果前一层的激活函数是Sigmoid,那么前一层的输出x1,x2,x3就恒为正值。
那么w1,w2,w3的更新量就取决于dL/dh1,要么全为正,要么全为负。也就是说这些w要么都往正向移动,要么都往负向移动。
然而最佳的移动路线有可能是有些往正向移动,有些往负向移动。恒正恒负的移动方式就产生了震荡。降低了收敛速度。
权重移动的示意图如下,其中绿色为最佳移动方向,红色则为恒正恒负的移动方式。
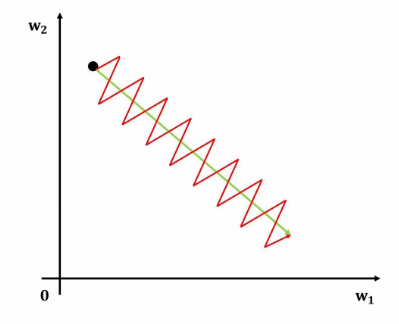
4.2 梯度分析
如果你对这几个函数进行求导,会发现得到的导数的公式十分复杂,这不利于运算效率。幸运的是,这些常见的激活函数可以通过它们的输出来表达导数,其计算将变得非常简洁。工业界目前采用的都是这种做法。其导数计算方法如下:
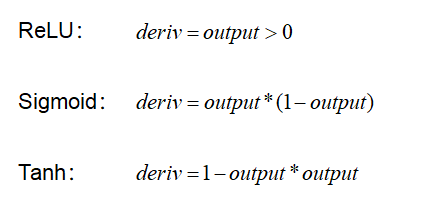
我们以Sigmoid函数为例验证一下上述结论:
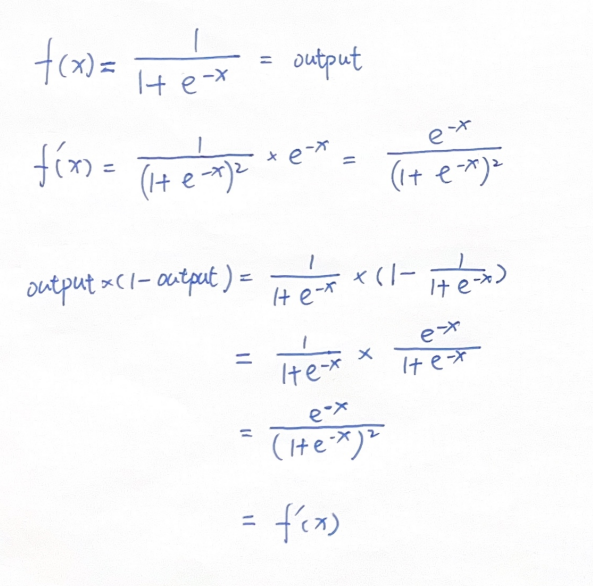
三个激活函数的导数图像如下:
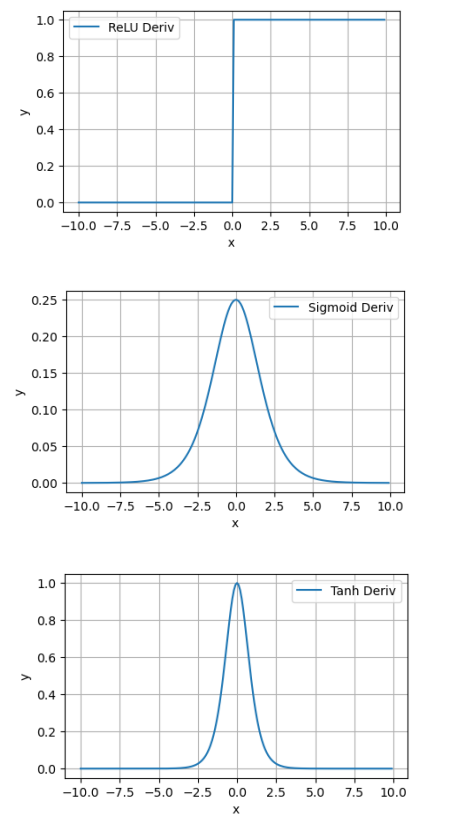
ReLU函数没有饱和区,相比于Sigmoid或Tanh等激活函数,ReLU在正区域不会导致梯度消失,这使得网络在深层次训练中能够更好地传播梯度,避免训练停滞。
但同时ReLU函数 存在“死亡ReLU”问题:当输入为负时,输出为0,导数也为 0,可能导致某些神经元无法更新。
Sigmoid平滑且可导,便于优化。当输入绝对值较大时,梯度趋近于0,导致梯度消失问题,从而影响深层网络的训练。
Tanh的导数在输入接近零时较大,梯度消失问题比Sigmoid更轻。但当输入绝对值较大时,梯度仍然会趋近于0,导致训练缓慢。
4.3 计算复杂度
ReLU函数计算简单,没有复杂的指数运算。ReLU的计算非常简单,只是判断输入是否为正,因此计算效率非常高,尤其适合深度网络中的大规模计算。
Sigmoid和Tanh函数计算复杂度较高(涉及指数运算),尤其是在大规模网络中。
4.4 应用场景
ReLU对梯度的”保持“作用,能有效避免梯度消失和梯度爆炸哦,广泛应用于深度学习的隐藏层。
Sigmoid因其输出范围(0,1),常用于二分类问题的输出层,主要用于逻辑回归和早期的神经网络模型。
Tanh常用于神经网络的隐藏层,因为它能够将输入映射到(-1, 1)的范围内,适合处理数据。
5. Softmax
最后我们来看一个比较特殊的激活函数,他不是作用于单个神经元节点,对单个变量进行映射,而是将一组实数值转换为概率分布,所有输出值加起来等于1。
函数定义:
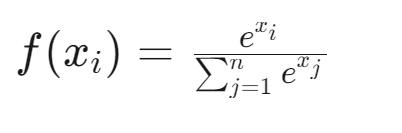
Softmax函数能够提供明确的概率解释,很好地处理多分类任务。《Grokking Deep Learning》by Andrew W.Trask 一书中举的例子可以很好的反映Softmax函数的作用。
在MNIST图像集的分类中,假如我们在最后一层输出如下:

预测结果表明这张图必然是数字”9“。
当我们用Sigmoid函数做输出节点激活时,结果变成了:

当然我们也能判断数字是9,但是其他的数字竟然也获得了0.5的概率?很显然这不太合理。
如果用Softmax,则结果就合理很多:

因此,Softmax函数通常用于结果互斥的多分类问题输出层。常与交叉熵损失函数一起使用。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号