最优化理论-1——阻尼牛顿法

算法思想

由于实际问题的精确极小点一般是不知道的, 因此初始点的选取给算法的实际操作带来了很大的困难. 为了克服这一困难, 可引入线搜索技术以得到大范围收敛的算法, 即所谓的阻尼牛顿法.
算法步骤

基于 Armijo 搜索的阻尼牛顿法如下:

代码：

点击查看代码

function [x,val,k]=dampnm(fun,gfun, Hess,x0)
%功能: 用阻尼牛顿法求解无约束问题:  min f(x)
%输入: x0是初始点, fun, gfun, Hess 分别是求
%         目标函数,梯度,Hesse 阵的函数
%输出:  x, val分别是近似最优点和最优值,  k是迭代次数.
maxk=100;   %给出最大迭代次数
rho=0.55;sigma=0.4;
k=0;  epsilon=1e-5;
while(k<maxk)
    gk=feval(gfun,x0); %计算梯度
    Gk=feval(Hess,x0);  %计算Hesse阵
    dk=-Gk\gk; %解方程组Gk*dk=-gk, 计算搜索方向
    if(norm(gk)<epsilon), break; end  %检验终止准则
    m=0; mk=0;
    while(m<20)   % 用Armijo搜索求步长 
        if(feval(fun,x0+rho^m*dk)<feval(fun,x0)+sigma*rho^m*gk'*dk)
            mk=m; break;
        end
        m=m+1;
    end
    x0=x0+rho^mk*dk;
    k=k+1;
end
x=x0;
val=feval(fun,x); 
%gval=norm(gfun(x));

示例

考虑无约束优化问题

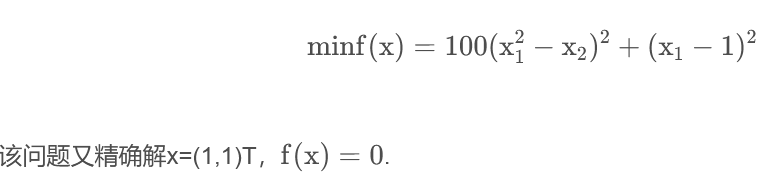
点击查看代码

%目标函数
function f=fun(x)
f=100*(x(1)^2-x(2))^2+(x(1)-1)^2;

%梯度
function gf=gfun(x)
gf=[400*x(1)*(x(1)^2-x(2))+2*(x(1)-1), -200*(x(1)^2-x(2))]’;
%Hesse 阵
function He=Hess(x)
n=length(x);
He=zeros(n,n);
He=[1200*x(1)^2-400*x(2)+2,-400*x(1);-400*x(1),200];

%main
x0=[0 0]';
[x,val,k]=dampnm('fun','gfun','Hess',x0);
fprintf("x = \n");
disp(x);
fprintf("val = \n");
disp(val);
fprintf("k = \n");
disp(k);

求解结果：

————————————————
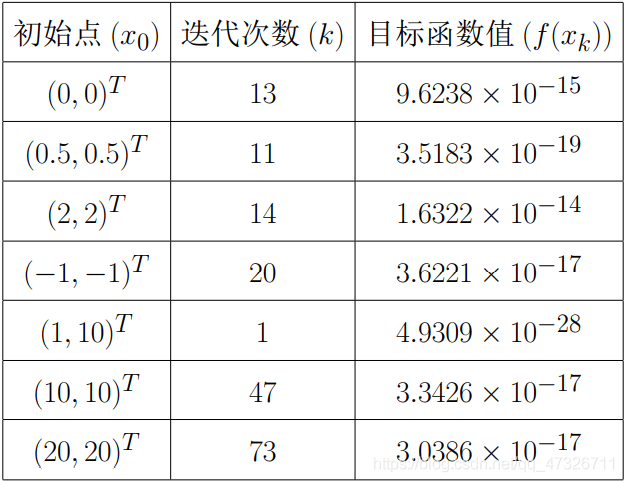
版权声明：本文为CSDN博主「斑马L*」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/qq_47326711/article/details/118075787