线性二次最优控制-状态调节器matlab


LQR状态调节器代码:
点击查看代码
function [u,x,y,Jmin,K,P,E] =LQ_adjustor( A,B,C,D,R,Q,x0,tmax,s1o2)
% A,B,C,D分别为系数矩阵; x0为初始状态向量,u为最优控制
% R为正定加权矩阵,Q为正半定加权矩阵,x为最优轨线,J为目标泛函值
% tmax为曲线图时间上限,s1o2=1为状态调节器;s1o2=2为输出调节器
syms t; % 定义符号变量t
if(s1o2==2)
Q=C'*Q*C;
end
[K,P,E]=lqr(A,B,Q,R); %求黎卡提方程矩阵P,状态反馈阵K及特征值E
AK=A-B*K; %调节器系统矩阵
Phit=expm(AK*t); % 状态转移矩阵
x=simplify(Phit*x0); %最优轨线
u=simplify(-K*x); %最优控制
Jmin=x0'*P*x0/2; %最小目标泛函值
y=simplify(C*x+D*u); %输出响应
q=size(C,1);n=size(x0);
for k=1:n
subplot(2,2,k);ezplot(t,x(k),[0,tmax],1);grid;title(' ')
xlabel('时间 t ')
ylabel('状态 x')
end
for k=1:q
subplot(2,2,k);ezplot(t,y(k),[0,tmax],2); grid;title(' ')
xlabel('时间 t ')
ylabel('输出量 y ')
end
end
主程序代码:
点击查看代码
A = [0 2;1 1];
b = [1;0];
C = [0 1];
D = 0;
x0 = [2;1]; %系统输入状态
Q = [5 0;0 0]; %动态状态误差加权系数矩阵
R = 1; %动态控制加权系数
tmax = 10; %tmax为曲线图时间上限
slo2 = 1; %s1o2=1为状态调节器;s1o2=2为输出调节器
[u,x,y,Jmin,K,P,E] = LQ_adjustor(A,b,C,D,R,Q,x0,tmax,slo2);
fprintf("最优控制律 u =\n"); disp(u) ;
fprintf("输出 x = \n");disp(x) ;
fprintf("输出量 y = \n");disp(y) ;
fprintf("最小目标泛函值 J= \n");disp(Jmin) ;
fprintf("状态反馈矩阵 k = \n");disp(K) ;
fprintf("黎卡提代数方程的解 P = \n");disp(P) ;
fprintf("调节器系统的特征 E = \n");disp(E) ;
结果:
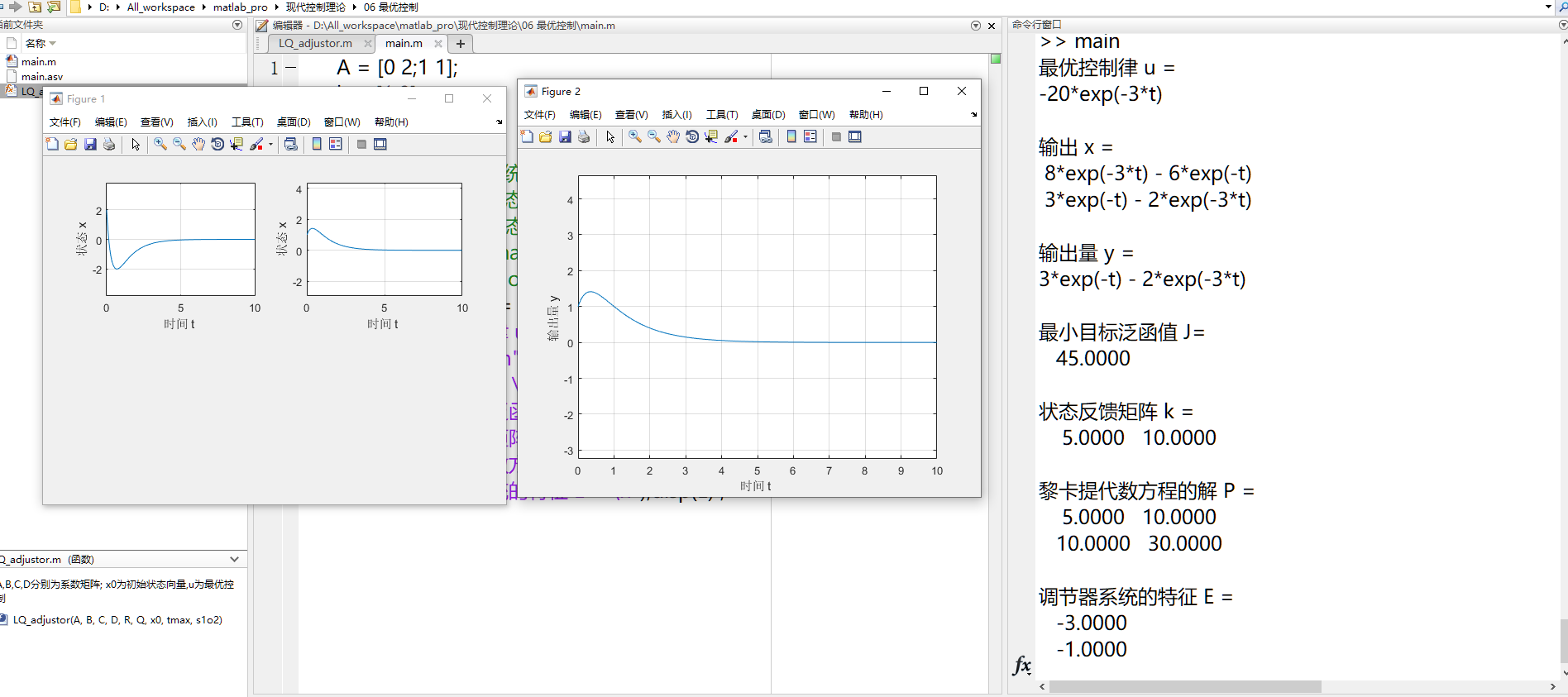
本文来自博客园,作者:相对维度,转载请注明原文链接:https://www.cnblogs.com/wangjirui/p/16577985.html


 浙公网安备 33010602011771号
浙公网安备 33010602011771号