回溯算法
参考:代码随想录,力扣
回溯算法能解决如下问题:
- 组合问题:N个数里面按一定规则找出k个数的集合
- 排列问题:N个数按一定规则全排列,有几种排列方式
- 切割问题:一个字符串按一定规则有几种切割方式
- 子集问题:一个N个数的集合里有多少符合条件的子集
- 棋盘问题:N皇后,解数独等等
回溯算法的模板:
void backtracking(参数) { if (终止条件) { 存放结果; return; } for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) { 处理节点; backtracking(路径,选择列表); // 递归 回溯,撤销处理结果 } }
类型一:组合问题
1. 给定两个整数 n 和 k,返回 1 ... n 中所有可能的 k 个数的组合。
示例:
输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]
本题这是回溯法的经典题目。
直接的解法当然是使用for循环,例如示例中k为2,很容易想到 用两个for循环,这样就可以输出 和示例中一样的结果。
int n = 4; for (int i = 1; i <= n; i++) { for (int j = i + 1; j <= n; j++) { System.out.println( i + " " + j); } }
k=2 需要两层循环,但k=50,那这。。。
使用回溯算法:
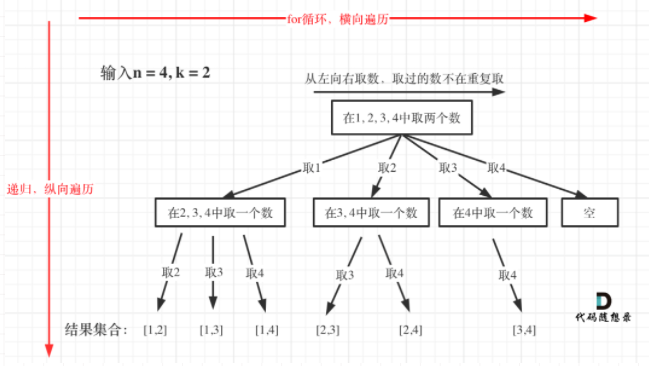
结合上图说下大体思想,回溯与DFS递归算法结合,dfs有参数begin表示开始的位置,也就是选中的值,从1到 n 。每次递归执行dfs就会把新的begin保存到 Deque<Integer> path 也就是双向队列之中。因为数字不能重复,第一个数字选择1,下一次dfs就要从2开始。在本题中取完[1,2],path长度与k相等,我们的得到第一种结果[1,2]。这是我们想得到下一种情况,就需要在递归语句执行后(本次递归中已经把这种情况写入ans中)把2吐出来,方便下次得到[1,3]这就是回溯。
public class Solution { public List<List<Integer>> combine(int n, int k) { List<List<Integer>> res = new ArrayList<>(); if (k <= 0 || n < k) { return res; } // 从 1 开始是题目的设定 Deque<Integer> path = new ArrayDeque<>(); dfs(n, k, 1, path, res); return res; } private void dfs(int n, int k, int begin, Deque<Integer> path, List<List<Integer>> res) { // 递归终止条件是:path 的长度等于 k if (path.size() == k) { res.add(new ArrayList<>(path)); return; } // 遍历可能的搜索起点 for (yinweiwomenint i = begin; i <= n; i++) { // 向路径变量里添加一个数 path.addLast(i); // 下一轮搜索,设置的搜索起点要加 1,因为组合数理不允许出现重复的元素 dfs(n, k, i + 1, path, res); // 重点理解这里:深度优先遍历有回头的过程,因此递归之前做了什么,递归之后需要做相同操作的逆向操作 path.removeLast(); } } }
组合问题类型二:
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
- 所有数字(包括 target)都是正整数。
- 解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
示例 2:
输入:candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
本题没有数量要求,元素可以重复,所以推出条件target<=0即可。同时执行下次递归式,从本次元素开始表示可重复。
public class Solution { public List<List<Integer>> combinationSum(int[] candidates, int target) { int len = candidates.length; List<List<Integer>> res = new ArrayList<>(); if (len == 0) { return res; } Deque<Integer> path = new ArrayDeque<>(); dfs(candidates, 0, len, target, path, res); return res; } /** * @param candidates 候选数组 * @param begin 搜索起点 * @param len 冗余变量,是 candidates 里的属性,可以不传 * @param target 每减去一个元素,目标值变小 * @param path 从根结点到叶子结点的路径,是一个栈 * @param res 结果集列表 */ private void dfs(int[] candidates, int begin, int len, int target, Deque<Integer> path, List<List<Integer>> res) { // target 为负数和 0 的时候不再产生新的孩子结点 if (target < 0) { return; } if (target == 0) { res.add(new ArrayList<>(path)); return; } // 重点理解这里从 begin 开始搜索的语意 for (int i = begin; i < len; i++) { path.addLast(candidates[i]); // 注意:由于每一个元素可以重复使用,下一轮搜索的起点依然是 i,这里非常容易弄错 dfs(candidates, i, len, target - candidates[i], path, res); // 状态重置 path.removeLast(); } } }
组合总和类型三:
给定一个数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用一次。
说明:
所有数字(包括目标数)都是正整数。
解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
示例 2:
输入: candidates = [2,5,2,1,2], target = 5,
所求解集为:
[
[1,2,2],
[5]
]
本题不能有重复的结果,比如示例二有三个二,不能说结果里面有三组[1,2,2],完了你告诉我说这三个二不一样。
我们要往递归树那里考虑,先把元素排序,三个二连着,这三组[1,2,2]对应什么样的树呢,

通过上图分析,同排集合相同,最左侧相同集合([1,2])的子树会完全包含右侧相同集合([1,2])的子树,最左侧[1,2]及右侧子节点形成的子树与中间[1,2]生成子树完全一致。
所以如果递归到元素2这里时,只要判断2是不是所有2中开头的2就可以了,不是的话直接continue;那么怎么体现是所有2的首位呢,使用used数组记录进入path的节点,条件是元素前面的节点不能与自身相等并且没有进入path,也就是used[i-1]是不是false.种情况叫做“树层去重”,会经常遇到。
树层去重==used[]
public class Solution { public List<List<Integer>> combinationSum2(int[] candidates, int target) { List<List<Integer>> res=new ArrayList<>(); if(target<=0||candidates.length<=0)return res; Deque<Integer> path=new ArrayDeque<>(); Arrays.sort(candidates); boolean[] used = new boolean[candidates.length]; dfs(candidates,target,0,path,res,used); return res; } private void dfs(int[] candidates, int target, int begin, Deque<Integer> path, List<List<Integer>> res,boolean[] used) { if(target<=0||begin==candidates.length){ if(target==0){ res.add(new ArrayList(path)); } return; } for(int i=begin;i<candidates.length;i++){ if(i>0&&candidates[i]==candidates[i-1]&&used[i-1]==false) continue; used[i]=true; path.addLast(candidates[i]); dfs(candidates,target-candidates[i],i+1,path,res,used); used[i]=false; path.removeLast(); } } }
切割问题:
给定一个字符串 s,将 s 分割成一些子串,使每个子串都是回文串。
返回 s 所有可能的分割方案。
示例:
输入: "aab"
输出:
[
["aa","b"],
["a","a","b"]
]
切割问题与组合问题十分类似,对比一下:
- 组合问题:选取一个a之后,在bcdef中再去选取第二个,选取b之后在cdef中在选取第三个.....。
- 切割问题:切割一个a之后,在bcdef中再去切割第二段,切割b之后在cdef中在切割第三段.....。
切割线的体现:
在处理组合问题的时候,递归参数需要传入startIndex,表示下一轮递归遍历的起始位置,这个startIndex就是切割线。
我们需要单独写个方法判断现在切出来的是否是回文串,就是把最前和最后比较,然后依次向内来一位。不一致就false。
public class Solution { private boolean checkPalindrome(String s,int left,int right){ while(left<right){ if(s.charAt(left)!=s.charAt(right)){ return false; } left++; right--; } return true; } public List<List<String>> partition(String s) { List<List<String>> ans=new ArrayList<>(); if(s.length()==0)return ans; Deque<String> path=new ArrayDeque<>(); dfs(s,0,path,ans); return ans; } private void dfs(String s, int begin, Deque<String> path, List<List<String>> ans) { if(begin==s.length()){ ans.add(new ArrayList<>(path)); return; } for(int i=begin;i<s.length();i++){ if(!checkPalindrome(s,begin,i)) continue; path.addLast(s.substring(begin,i+1)); dfs(s,i+1,path,ans); path.removeLast(); } } }
子集问题:
子集类型一:
给定一组不含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例: 输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
如果子集问题和切割问题是要递归树的叶节点,那么子集问题就是要所有节点(去重)
普通的去重就是再for循环中从startIndex 开始就可以了。
public class Solution { public List<List<Integer>> subsets(int[] nums) { List<List<Integer>> ans=new ArrayList<>(); if(nums.length==0)return ans; Deque<Integer> path=new ArrayDeque<>(); dfs(nums,0,path,ans); return ans; } private void dfs(int[] nums, int begin, Deque<Integer> path, List<List<Integer>> ans) { ans.add(new ArrayList(path)); for(int i=begin;i<nums.length;i++){ path.addLast(nums[i]); dfs(nums,i+1,path,ans); path.removeLast(); } } }
子集类型二:
给定一个可能包含重复元素的整数数组 nums,返回该数组所有可能的子集(幂集)。
说明:解集不能包含重复的子集。
示例:
输入: [1,2,2]
输出:
[
[2],
[1],
[1,2,2],
[2,2],
[1,2],
[]
]
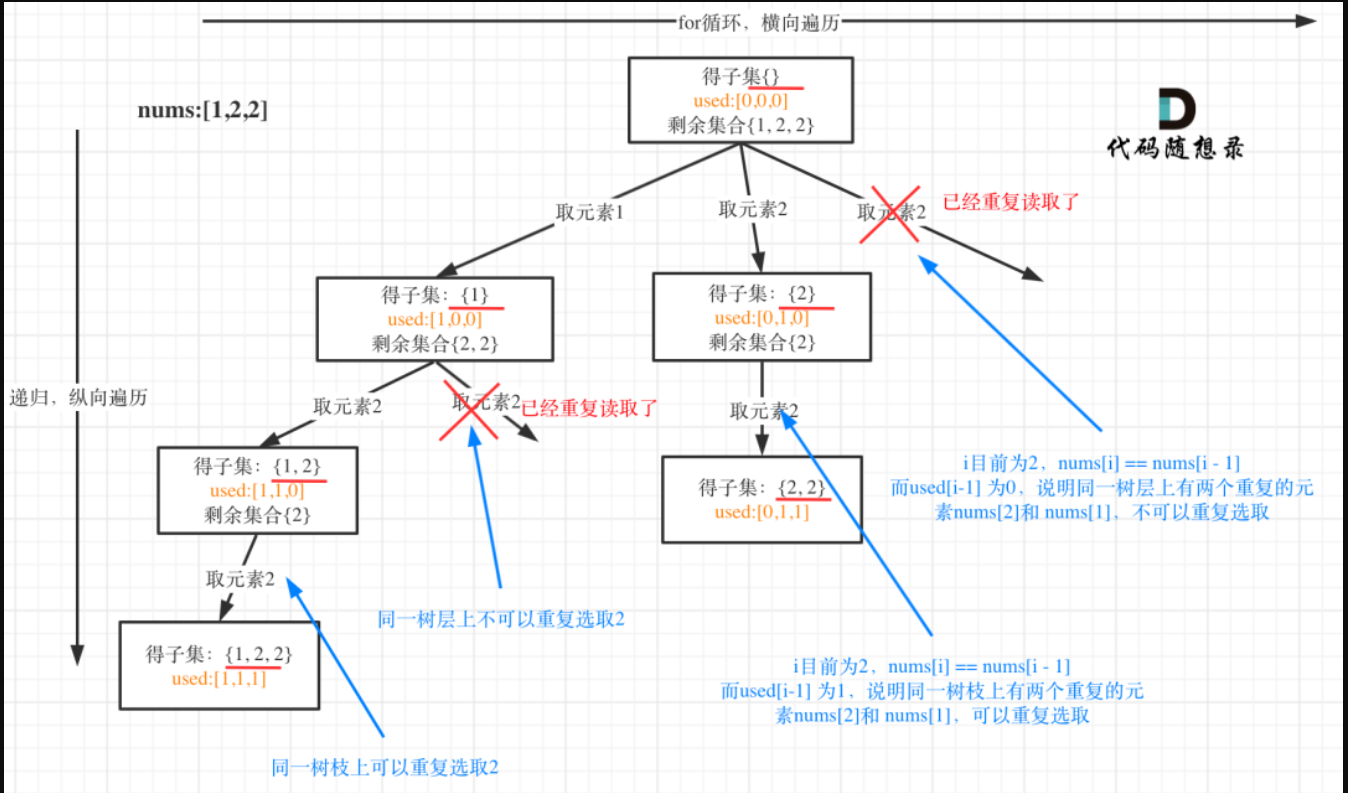
集合本身有重复元素,要求不同有重复子集,就是之前遇到的普通降重+树层去重就可以满足了,不要忘了先把结合排序。
class Solution { public List<List<Integer>> subsetsWithDup(int[] nums) { List<List<Integer>> ans=new ArrayList<>(); if(nums.length==0)return ans; Deque<Integer> path=new ArrayDeque<>(); Arrays.sort(nums); boolean[] used = new boolean[nums.length]; dfs(nums,0,path,ans,used); return ans; } private void dfs(int[] nums, int begin, Deque<Integer> path, List<List<Integer>> ans,boolean[] used) { ans.add(new ArrayList(path)); for(int i=begin;i<nums.length;i++){ if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false) continue; used[i]=true; path.addLast(nums[i]); dfs(nums,i+1,path,ans,used); used[i]=false; path.removeLast(); } } }
递增子序列:
示例:
输入: [4, 6, 7, 7] 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]
说明:
- 给定数组的长度不会超过15。
- 数组中的整数范围是 [-100,100]。
- 给定数组中可能包含重复数字,相等的数字应该被视为递增的一种情况。
本体最大的问题在于给的数组是没有排序的,我们之前的排序后树层去重解决不了相同元素不在一起的情况,比如[1,2,3,1,1,1]
所以在每一层都设置一个set,专门去除重复元素。
class Solution { // 定义全局变量保存结果 List<List<Integer>> res = new ArrayList<>(); public List<List<Integer>> findSubsequences(int[] nums) { // idx 初始化为 -1,开始 dfs 搜索。 dfs(nums, -1, new ArrayList<>()); return res; } private void dfs(int[] nums, int idx, List<Integer> curList) { // 只要当前的递增序列长度大于 1,就加入到结果 res 中,然后继续搜索递增序列的下一个值。 if (curList.size() > 1) { res.add(new ArrayList<>(curList)); } // 在 [idx + 1, nums.length - 1] 范围内遍历搜索递增序列的下一个值。 // 借助 set 对 [idx + 1, nums.length - 1] 范围内的数去重。 Set<Integer> set = new HashSet<>(); for (int i = idx + 1; i < nums.length; i++) { // 1. 如果 set 中已经有与 nums[i] 相同的值了,说明加上 nums[i] 后的所有可能的递增序列之前已经被搜过一遍了,因此停止继续搜索。 if (set.contains(nums[i])) { continue; } set.add(nums[i]); // 2. 如果 nums[i] >= nums[idx] 的话,说明出现了新的递增序列,因此继续 dfs 搜索(因为 curList 在这里是复用的,因此别忘了 remove 哦) if (idx == -1 || nums[i] >= nums[idx]) { curList.add(nums[i]); dfs(nums, i, curList); curList.remove(curList.size() - 1); } } } }
排序问题:
排序而言,[1,2]和[2,1]是两种情况,此时递归树长这样:
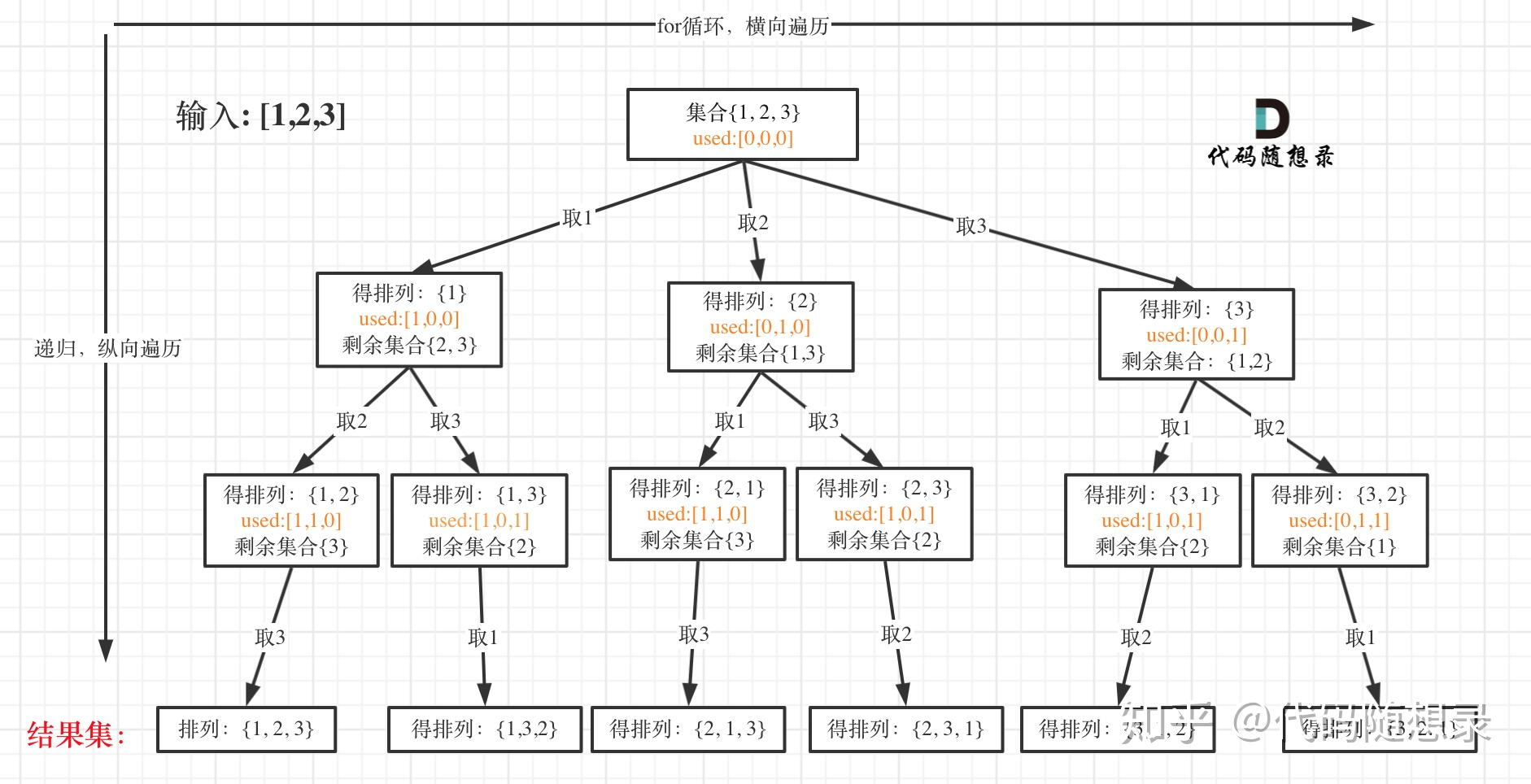
排序问题一:
给定一个 没有重复 数字的序列,返回其所有可能的全排列。
示例:
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
本体同样需要一个额外的used数组记录每个元素此时在不在path队列里里面 ,方法就是当把元素加入path时,把他的下标记录到used数组中,当元素从path中remove时,再更改used数组。
class Solution { public List<List<Integer>> permute(int[] nums) { List<List<Integer>> ans=new ArrayList<>(); if(nums.length==0)return ans; Deque<Integer> path=new ArrayDeque<>(); boolean[] used = new boolean[nums.length]; dfs(nums,0,path,ans,used); return ans; } private void dfs(int[] nums, int begin, Deque<Integer> path, List<List<Integer>> ans,boolean[] used) { if(path.size()==nums.length){ ans.add(new ArrayList(path)); return; } for(int i=0;i<nums.length;i++){ if (!used[i]) { path.addLast(nums[i]); used[i] = true; dfs(nums, i + 1, path, ans,used); // 注意:下面这两行代码发生 「回溯」,回溯发生在从 深层结点 回到 浅层结点 的过程,代码在形式上和递归之前是对称的 used[i] = false; path.removeLast(); } } } }
排序问题二:
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
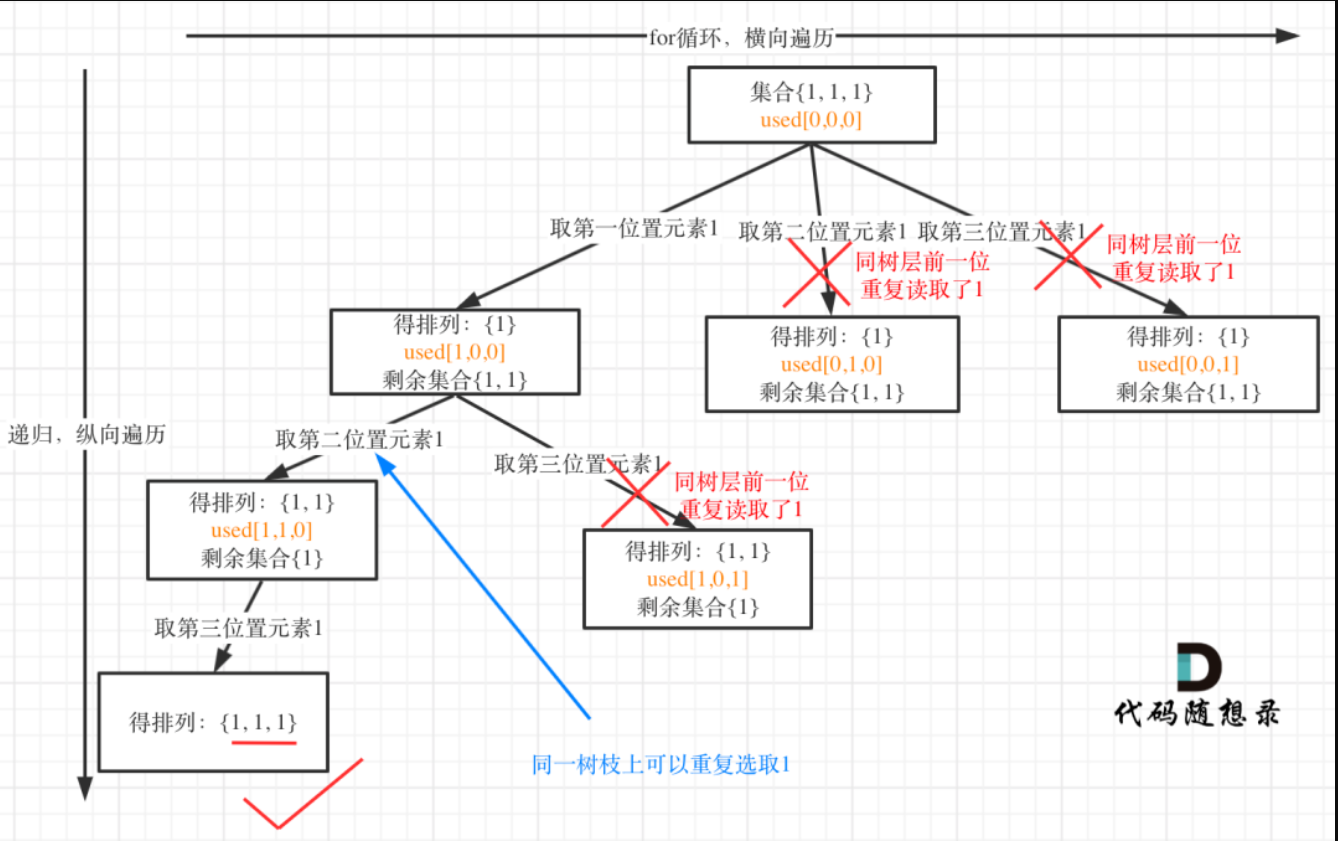
class Solution { public List<List<Integer>> permuteUnique(int[] nums) { List<List<Integer>> ans=new ArrayList<>(); if(nums.length==0)return ans; Deque<Integer> path=new ArrayDeque<>(); boolean[] used = new boolean[nums.length]; Arrays.sort(nums); dfs(nums,0,path,ans,used); return ans; } private void dfs(int[] nums, int begin, Deque<Integer> path, List<List<Integer>> ans,boolean[] used) { if(path.size()==nums.length){ ans.add(new ArrayList(path)); return; } for(int i=0;i<nums.length;i++){ if (!used[i]) {//因为是从开始,把以前进过path[] 刨出去 if(i>0&&nums[i]==nums[i-1]&&used[i-1]==false) continue; path.addLast(nums[i]); used[i] = true; dfs(nums, i + 1, path, ans,used); // 注意:下面这两行代码发生 「回溯」,回溯发生在从 深层结点 回到 浅层结点 的过程,代码在形式上和递归之前是对称的 used[i] = false; path.removeLast(); } } } }
棋盘问题:(N皇后)
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给定一个整数 n,返回所有不同的 n 皇后问题的解决方案。
每一种解法包含一个明确的 n 皇后问题的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例: 输入: 4
输出: [
[".Q..", // 解法 1
"...Q",
"Q...",
"..Q."],
["..Q.", // 解法 2
"Q...",
"...Q",
".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。
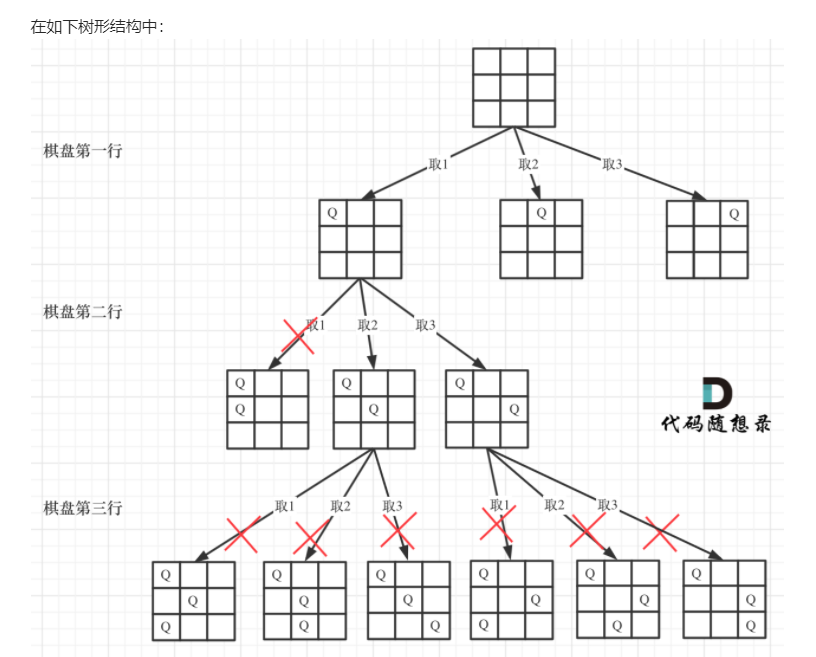
n皇后和上面我们一直做的题目没有本质区别,如果每一次遍历只看这特定的一行。
棋盘的宽度就是for循环的长度,递归的深度就是棋盘的高度,这样就可以套进回溯法的模板里了。
代码实现:
class Solution { public List<List<String>> solveNQueens(int n) { List<List<String>> result = new ArrayList<>(); List<char[]> board = new ArrayList<>(); for (int i = 0; i < n; i++) { char[] chars = new char[n]; Arrays.fill(chars, '.'); board.add(chars); }//初始化全部都是 . 的空棋盘 // n 为输入的棋盘大小 // row 是当前递归到***的第几行了 backtracking(n, 0, board, result); //其实本题更像一维的数组,先在第一行[0-n]选一个,每一个下面[0-n]接着选,不合格剪掉,只是最终结果节点二维的。 return result; } private void backtracking(int n, int row, List<char[]> board, List<List<String>> result) { if (n == row) { List<String> path = new ArrayList<>(); for (char[] chars : board) { path.add(new String(chars)); } result.add(path); return; } for (int col = 0; col < n; col++) { if (isValid(row, col, n, board)) {// 验证合法就可以放 board.get(row)[col] = 'Q';// 放置皇后 backtracking(n, row + 1, board, result); board.get(row)[col] = '.';// 回溯,撤销皇后 } } } private boolean isValid(int row, int col, int n, List<char[]> board) { //检查是否可以在row行col列放皇后不冲突,因为皇后是先放一行再放下一行,所以在行上皇后必不冲突 //只需检查列上,以及45° 135°对角线是否冲突 for (int i = 0; i < row; i++) { // 检查列 if (board.get(i)[col] == 'Q') { return false; } } for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) { // 检查 45度角是否有皇后 if (board.get(i)[j] == 'Q') { return false; } } for (int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) { // 检查 135度角是否有皇后 if (board.get(i)[j] == 'Q') { return false; } } return true; } }

 浙公网安备 33010602011771号
浙公网安备 33010602011771号