大小比较

前言

高中数学中涉及大小比较的数学素材和知识点比较多，是高中数学中比较常见的一种题型，在不等式、函数、定积分，以及构造函数中，都会见到其影子，现对其进行整理，以便于学习。

理论依据

• 利用作差法或作商法比较大小；比较代数式大小，判断数列的单调性；

• 利用函数的单调性比较大小；可以利用现成的函数的单调性；

• 利用代数式的范围比较大小；此时可以利用二分法思想，将其范围压缩；

• 利用中间量比较大小；

• [高阶]构造函数，再利用其单调性比较大小；

常见类型

• 1、利用不等式性质，对代数式大小比较，

作差法^[1]或作商法，常用变形：平方做差法、取对数做差法等

【代数式】若\(P=\sqrt{a+2}+\sqrt{a+5}\)，\(Q=\sqrt{a+3}+\sqrt{a+4}(a\ge 0)\)，比较\(P、Q\)的大小。

分析：由于\(a\ge 0\)，\(P > 0\)，\(Q > 0\)，

则有\(Q^2-P^2=2a+7+2\sqrt{a^2+7a+12}-(2a+7+2\sqrt{a^2+7a+10})\)

\(=2(\sqrt{a^2+7a+12}- \sqrt{a^2+7a+10}) > 0\)，所以\(Q^2 > P^2\)，则\(Q > P\)。

试比较\(16^{18}\)和\(18^{16}\)的大小关系；

法1：作商法，\(\cfrac{16^{18}}{18^{16}}=(\cfrac{16}{18})^{16}\cdot 16^2=(\cfrac{8}{9})^{16}\cdot 2^8\)

\(=(\cfrac{64}{81})^{8}\cdot 2^8=(\cfrac{128}{81})^{8}>1\)，故\(16^{18}>18^{16}\)；

法2：取对数作差法，\(lg16^{18}-lg18^{16}=18lg16-16lg18\)

\(=72lg2-16(lg2+2lg3)=56lg2-32lg3>0\)，故\(16^{18}>18^{16}\)；

• 2、利用具体函数的单调性进行大小比较，常用变形；

涉及函数有二次函数，指数函数，对数函数，幂函数，三角函数，此时大多只涉及一类函数，

【幂函数】 幂函数的图像经过点\((\cfrac{1}{2}，\cfrac{\sqrt{2}}{2})\)，若\(0< a < b < 1\)，试比较\(f(a)、f(b)、f(1)、f(\cfrac{1}{a})、f(\cfrac{1}{b})\)的大小。

分析：设幂函数解析式为\(y=x^{\alpha}\)，由 幂函数的图像经过点\((\cfrac{1}{2}，\cfrac{\sqrt{2}}{2})\)，

则\((\cfrac{1}{2})^{\alpha}=\cfrac{\sqrt{2}}{2}\)，即\(2^{-\alpha}=2^{-\frac{1}{2}}\)，故\(\alpha=\cfrac{1}{2}\)，故幂函数为\(y=x^{\frac{1}{2}}\)，

则其在定义域\([0，+\infty)\)上单调递增。又由于\(0 < a < b < 1\)，则可知\(\cfrac{1}{a}>\cfrac{1}{b}>1\)，

即\(0 < a < b < 1 <\cfrac{1}{b} < \cfrac{1}{a}\)，故有\(f(a) < f(b) < f(1) < f(\cfrac{1}{b}) < f(\cfrac{1}{a})\)。

【指数函数】设\(y_1=4^{0.7}\)，\(y_2=8^{0.45}\)，\(y_3=(\cfrac{1}{2})^{-1.5}\)，比较\(y_1，y_2，y_3\)的大小。

分析：\(y_1=4^{0.7}=2^{1.4}\)，\(y_2=8^{0.45}=2^{1.35}\)，\(y_3=(\cfrac{1}{2})^{-1.5}=2^{1.5}\)，

又\(y=2^x\)在\(R\)上单调递增，故\(y_2 < y_1 < y_3\)；

【幂、指数函数】设\(a=(\cfrac{3}{5})^{\frac{2}{5}}\)，\(b=(\cfrac{2}{5})^{\frac{3}{5}}\)，\(c=(\cfrac{2}{5})^{\frac{2}{5}}\)，试比较\(a、b、c\)的大小。

分析：比较\(a、c\)，利用幂函数\(y=x^{\cfrac{2}{5}}\)，在\((0，+\infty)\)上单调递增，故\(a > c\)；

比较\(b、c\)，利用指数函数\(y=(\cfrac{2}{5})^x\)，在\((-\infty，+\infty)\)上单调递减，故\(c > b\)；

故有\(a > c > b\)。

【三角函数】设\(a=\cfrac{1}{2}cos2^{\circ}-\cfrac{\sqrt{3}}{2}sin2^{\circ}\)，\(b=\cfrac{2tan14^{\circ}}{1-tan^214^{\circ}}\)，\(c=\sqrt{\cfrac{1-\cos50^{\circ}}{2}}\)，则有【】

$A.a < c < b$ $B.a < b < c$ $C.b < c < a$ $D.c < a < b$

分析：由题目可知，\(a=sin(30^{\circ}-2^{\circ})=sin28^{\circ}\)，\(b=tan28^{\circ}\)，\(c=sin25^{\circ}\)，

则\(c<a<b\)，故选\(D\)；

• 3、利用代数式的取值范围进行大小比较，此时涉及多个函数的单调性和值域问题；

涉及函数有二次函数，指数函数，对数函数，幂函数，三角函数，

设\(a=log_{\frac{1}{2}}2\)，\(b=ln\frac{\pi}{2}\)，\(c=2^{\frac{1}{\pi}}\)，试比较\(a、b、c\)的大小。

分析：\(a=log_{\frac{1}{2}}2 < 0\)，\(0< b=ln\frac{\pi}{2} < 1\)，\(c=2^{\frac{1}{\pi}} >1\)，

故有\(a < b < c\)。

若\(x\in (e^{-1}，1)\)，\(a=lnx\)，\(b=(\cfrac{1}{2})^{lnx}\)，\(c=e^{lnx}\)，则其大小关系为__________。

分析：借助赋值法，令\(x=\cfrac{1}{2}\)，

则可知\(b=(\cfrac{1}{2})^{lnx}>1\)，\(a=lnx<0\)，\(c=e^{lnx}=\cfrac{1}{2}\)，

故大小关系为\(b>c>a\)；

• 4、利用赋值法比较大小

【2019届高三理科数学三轮模拟试题】若\(0<a<b<1\)，则\(a^b\)，\(b^a\)，\(log_ba\)，\(log_ab\)的大小关系为【】

$A.a^b > b^a > log_ba > log_{\frac{1}{a}} b$ $B.b^a > a^b > log_{\frac{1}{a}} b> log_ba $

$C.log_ba > a^b > b^a >log_{\frac{1}{a}} b$ $D.log_ba > b^a > a^b >log_{\frac{1}{a}} b$

法1：赋值法，令\(a=\cfrac{1}{4}\)，\(b=\cfrac{1}{2}\)，计算比较得到， \(log_ba > b^a > a^b >log_{\frac{1}{a}} b\)，故选\(D\).

法2：不等式性质法，由于\(0<a<b<1\)，则\(1>b^a>a^a>a^b>0\)，\(log_ba>log_bb=1\)，

又由于\(0<a<1\)，则\(\cfrac{1}{a}>1\)，则\(log_{\frac{1}{a}} b<0\)，

综上， \(log_ba > b^a > a^b >log_{\frac{1}{a}} b\)，故选\(D\).

• 5、利用中间参量进行大小比较；

涉及函数有二次函数，指数函数，对数函数，幂函数，三角函数，此时只是单纯的一类函数，中间参量常常取\(0\)，\(1\)等这些简单而特殊的值。涉及指数函数时中间量常取\(1=a^0\)，涉及对数函数时中间量常取\(0=log_a1\)，

大小比较：\(log_23\)和\(log_34\)和\(log_45\)；详解

• 6、利用形进行大小比较；

可能会涉及图形的面积、体积、或长度、角度、直线的斜率等，

【数形结合】【导数的几何意义】已知函数 \(f(x)\) 的图象如图所示， \(f^{\prime}(x)\) 是 \(f(x)\) 的导函数， 则下列数值排序正确的是【\(\qquad\)】

$A$.$0< f'(2)< f'(3)< f(3)-f(2)$

$B.$$0< f'(3)< f'(2)< f(3)-f(2)$

$C.$$0< f'(3)< f(3)-f(2)< f'(2)$

$D.$$0< f(3)-f(2)< f'(2)< f'(3)$

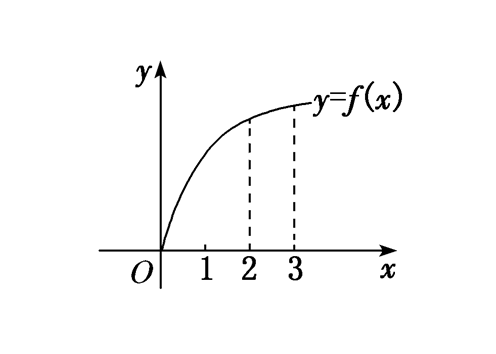
解析：设 \(f'(2)\)表示曲线在点\((2,f(2))\)处的切线的斜率， \(f'(3)\)表示曲线在点\((3,f(3))\)处的切线的斜率，\(f(3)\)\(-\)\(f(2)\)\(=\)\(\cfrac{f(3)-f(2)}{3-2}\)表示经过点\((2,f(2))\)和点\((3,f(3))\)的直线的斜率，故数形结合知 \(0\)\(<\)\(f'(3)\)\(<\)\(f(3)\)\(-\)\(f(2)\)\(<\)\(f'(2)\)， 故选 \(C\).

【定积分比较大小】若\(s_1=\displaystyle\int_{1}^{2}x^2\;dx\)，\(s_2=\displaystyle\int_{1}^{2}\cfrac{1}{x}\;dx\)，\(s_3=\displaystyle\int_{1}^{2}e^x\;dx\)，则\(S_1，S_2，S_3\)的大小关系如何？

法1：从数的角度，计算定积分的大小，从而比较大小，过程略。\(S_2 < S_1 < S_3\)。

法2：从形的角度，利用定积分的几何意义，借助图形的面积直观比较大小。\(S_2 < S_1 < S_3\)。

【选自2021届黄冈八模测试卷一第8题】设 \(x_{1}\)、 \(x_{2}\)、 \(x_{3}\) 均为实数， \((\cfrac{1}{3})^{x_{1}}\)\(=\)\(\log _{2}(x_{1}+1)\)，\((\cfrac{1}{3})^{x_{2}}\)\(=\)\(\log _{3}x_{2}\)，\((\cfrac{1}{3})^{x_{3}}\)\(=\)\(\log _{2}x_{3}\)， 则【\(\quad\)】

$A.x_{1}< x_{3}< x_{2}$ $B.x_{3}< x_{2}< x_{1}$ $C.x_{3}< x_{1}< x_{2}$ $D.x_{2}< x_{1}< x_{3}$

解析：做函数 \(y=(\cfrac{1}{3})^x\)，\(y=log_2(x+1)\)，\(y=log_3x\)，\(y=log_2x\)的大致图像，如图所示，

则三个交点的横坐标从左到右依次为\(x_1\)、\(x_3\)、\(x_2\)，

所以 \(x_{1}< x_{3}< x_{2}\) ，故选\(A\).

引申：若\(y_1=(\cfrac{1}{3})^{x_{1}}\)\(=\)\(\log _{2}(x_{1}+1)\)，\(y_2=(\cfrac{1}{3})^{x_{2}}\)\(=\)\(\log _{3}x_{2}\)，\(y_3=(\cfrac{1}{3})^{x_{3}}\)\(=\)\(\log _{2}x_{3}\)， 则由交点的纵坐标的高低位置可知，还可以判断得到 \(y_{1}> y_{3}> y_{2}\).

高阶拔高

• 7、利用线性规划进行大小比较；

已知 \(x,y>0\)，\(x+\cfrac{y}{3}>8\)，\(2x+\cfrac{5y}{3}<22\)，比较 \(x\) 和 \(y\) 的大小；

提示：首先做出可行域，令 \(z=x-y\)，从而转化为求 \(z\) 的取值范围问题； 答案\(x-y>0\)，即 \(x>y\) ;

• 8、构造函数进行大小比较；

涉及构造函数，大难点，抽象函数和具体函数，

【2017•渭南模拟】已知定义域为R的奇函数\(y=f(x)\)的导函数为\(y=f'(x)\)，当\(x> 0\)时，\(f'(x)+\cfrac{f(x)}{x}>0\)，若\(a=\cfrac{1}{3}f(\cfrac{1}{3})，b=-3f(-3)，c=(ln\cfrac{1}{3})f(ln\cfrac{1}{3})\)，则\(a，b，c\)的大小关系正确的是　 【 】

$A.a < b < c$ $B.a < c < b$ $C.b < c < a$ $D.c < a < b$

分析：当\(x> 0\)时，\(f'(x)+\cfrac{f(x)}{x}>0\)，即\(xf'(x)+f(x)>0\)，

故构造函数\(g(x)=x\cdot f(x)\)，由于\(y=f(x)\)与\(y=x\)都是奇函数，则函数\(g(x)\)为偶函数，

当\(x >0\)时，\(g'(x)=f(x)+xf'(x) >0\)，即函数\(g(x)\)在\([0，+\infty)\)上单调递增，

由偶函数可知，函数\(g(x)\)在\((-\infty，0]\)上单调递减。

而\(a=\cfrac{1}{3}f(\cfrac{1}{3})=g(\cfrac{1}{3})\)，

\(b=-3f(-3)=g(-3)=g(3)\)，

\(c=(ln\cfrac{1}{3})f(ln\cfrac{1}{3})=g(ln\cfrac{1}{3})=g(-ln3)=g(ln3)\)，

又\(\cfrac{1}{3} < ln3 < 3\)，故\(g(\cfrac{1}{3}) < g(ln3) < g(3)\)，即\(a < c < b\)，故选B.

【2020年全国卷Ⅱ卷理数第11题文数第12题】若\(2^x-2^{y}<3^{-x}-3^{-y}\)，则【\(\quad\)】

$A.\ln (y-x+1)>0$ $B.\ln (y-x+1)<0$ $C.\ln|x-y|>0$ $D.\ln|x-y|<0$

分析：要顺利解答本题目，需要先将原不等式作等价转化，\(2^x-3^{-x}<2^{y}-3^{-y}\)，

这样我们就能看到上述不等式的两端，是同结构的，故想到构造函数，

解析：令\(f(t)=2^t-3^{-t}\)，则\(t\in R\)，且\(f(t)\)在\(t\in R\)上单调递增\(y\)\(=\)\(2^t\)为增函数，\(y\)\(=\)\(-3^{-t}\)为增函数，增+增=增，故\(f(t)\)\(=\)\(2^t\)\(-\)\(3^{-t}\)为增函数。单调性的给出方式，

故原不等式等价于\(f(x)<f(y)\)，由\(f(t)\)单调递增，得到\(x<y\)，

故\(y-x>0\)，\(y-x+1>1\)，则\(ln(y-x+1)>0\)；故选\(A\)；

【2020年新课标Ⅰ理科数学第\(12\)题】【上例的延申题】 若 \(2^{a}+\log_{2}a=4^{b}+2\log_{4}b\)， 则 【\(\quad\)】

$A.a > 2b$ $B.a < 2b$ $C.a > b^2$ $D.a < b^2$

解析：因为 \(2^{a}+\log _{2} a=4^{b}+2 \log _{4} b=2^{2 b}+\log _{2}b\)，

又由于 \(2^{2b}+\log_{2}b<2^{2b}+\log_{2}2b=2^{2b}+\log_{2}b+1\)，

故 \(2^{a}+\log_{2}a<2^{2b}+\log_{2}2b\)，

此时令 \(f(x)=2^{x}+\log_{2}x\)， 则上述条件变化为 \(f(a)<f(2b)\)这样就能利用新构造的函数的性质比较大小，此时主要用到定义域和单调性。\(\quad\)，

由指对数函数的单调性可得 \(f(x)\) 在 \((0,+\infty)\) 内单调递增，且 \(f(a)<f(2b)\)，

则得到 \(a<2b\)，故选：\(B\) .

【构造函数+大小比较】【2017\(\cdot\)河南平顶山一模】已知\(f(x)\)是定义在\((0，+\infty)\)上的函数，对任意两个不相等的正数\(x_1，x_2\)，都有\(\cfrac{x_2f(x_1)-x_1f(x_2)}{x_1-x_2}>0\)，记\(a=\cfrac{f(3^{0.2})}{3^{0.2}}\)，\(b=\cfrac{f(0.3^2)}{0.3^2}\)，\(c=\cfrac{f(log_25)}{log_25}\)，则【】

$A.a < b < c$ $B.b < a < c$ $C.c < a < b$ $D.c < b < a$

分析：注意到\(a，b，c\)的结构，由题目猜想：要构造的函数是\(g(x)=\cfrac{f(x)}{x}\)，

那么是否正确，以下做以验证。

令\(0< x_1< x_2\)，则由单调性定义的等价形式可得，

\(\cfrac{g(x_1)-g(x_2)}{x_1-x_2}=\cfrac{\cfrac{f(x_1)}{x_1}-\cfrac{f(x_2)}{x_2}}{x_1-x_2}=\cfrac{x_2f(x_1)-x_1f(x_2)}{x_1x_2(x_1-x_2)}\)

由题目，对任意两个不相等的正数\(x_1，x_2\)，都有\(\cfrac{x_2f(x_1)-x_1f(x_2)}{x_1-x_2} >0\)，

则可知\(\cfrac{g(x_1)-g(x_2)}{x_1-x_2} >0\)，即函数\(g(x)=\cfrac{f(x)}{x}\)是单调递增的，

故题目需要我们比较\(g(3^{0.2})\)，\(g(0.3^2)\)，\(g(log_25)\)这三个的大小关系，

只需要比较自变量的大小就可以了；

由于\(1=3^0 < 3^{0.2} < 3^{0.5}=\sqrt{3} <2\)，\(0 < 0.3^2=0.09 <1\)，\(log_25 > log_24=2\)，

故\(g(0.3^2) < g(3^{0.2}) < g(log_25)\)，即\(b < a < c\)。故选\(B\).

需要记忆

下述结论中的结论2和结论3，在函数与导数的高阶考察中常常会作为变形的基础，故需要认真理解记忆。

【三角函数比较大小】三角函数章节中的重要不等式：\(\theta\in (0，\cfrac{\pi}{2})\)时，\(sin\theta < \theta < tan\theta\)。

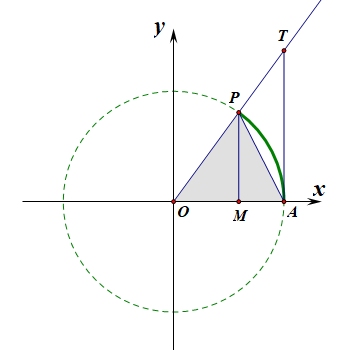
【证法1】：三角函数线法，如图所示为单位圆，则\(sin\theta=MP\)，\(tan\theta=AT\)，\(\overset{\frown}{AP}=\theta\cdot 1=\theta\)

由图可知，\(S_{\Delta OAP} < S_{扇形 OAP} < S_{\Delta OAT}\)

即\(\cfrac{1}{2}\cdot |OA|\cdot MP < \cfrac{1}{2}\cdot \theta \cdot |OA| <\cfrac{1}{2}\cdot |OA|\cdot AT\)

则有\(MP < \theta < AT\)，即\(sin\theta < \theta < tan\theta\)。

故\(\theta\in (0，\cfrac{\pi}{2})\)时，\(sin\theta < \theta < tan\theta\)。

【证法2】：构造函数法，如令\(g(x)=sinx-x\)，\(x\in (0，\cfrac{\pi}{2})\)，

则\(g'(x)=cosx-1\leq 0\)恒成立，故\(g(x)\)在\(x\in (0，\cfrac{\pi}{2})\)上单调递减，

故\(g(x) < g(0)=0\)，即\(sinx < x\)，同理可证\(x < tanx\)，

故\(\theta\in (0，\cfrac{\pi}{2})\)时，\(sin\theta < \theta < tan\theta\)。

\(e^x>x+1(x\neq 0)\)

证明思路：【法1】数形结合法，令\(f(x)=e^x\)，\(g(x)=x+1\)，在同一个坐标系中作出这两个函数的图像，

由图像可知，当\(x\neq 0\)时，都满足关系\(e^x>x+1\)。

补充：至于函数\(f(x)=e^x\)和函数\(g(x)=x+1\)为什么会相切与点\((0，1)\)，

我们可以用导数方法来解答。

【法2】作差构造函数法，令\(h(x)=e^x-x-1\)，则\(h'(x)=e^x-1\) ，

当\(x<0\)时，\(h'(x)<0\)；当\(x>0\)时，\(h'(x)>0\)；

即函数\(h(x)\)在\((-\infty，0)\)上单调递减，在\((0，+\infty)\)上单调递增，

故函数\(h(x)_{min}=h(0)=0\)，故\(h(x)\ge 0\)，当且仅当\(x=0\)时取到等号，

故\(x\neq 0\)时，总有\(h(x)>0\)，即\(e^x>x+1\)。

证明： \(lnx\leq x-1(x>0)\)

证明思路：【法1】数形结合法，令\(f(x)=lnx\)，\(g(x)=x-1\)，

在同一个坐标系中作出这两个函数的图像，

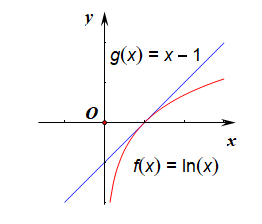
由图像可知，当\(x> 0\)时，都满足关系\(lnx\leq x-1\)。

【法2】：作差构造函数法，令\(h(x)=lnx-x+1(x>0)\)，则\(h'(x)=\cfrac{1}{x}-1\)，

当\(0<x<1\)时，\(h'(x)>0\)；当\(x>1\)时，\(h'(x)<0\)；

即函数\(h(x)\)在\((0，1)\)上单调递增，在\((1，+\infty)\)上单调递减，

故函数\(h(x)_{max}=h(1)=0\)，故\(h(x)\leq 0\)，当且仅当\(x=1\)时取到等号，

故\(x> 0\)时，总有\(h(x)\leq 0\)，即\(lnx\leq >x-1\)。

【法3】利用反函数法，此法主要基于\(e^x\ge x+1\)的结论，

由于函数\(y=e^x\)以及函数\(y=x+1\)关于直线\(y=x\)的对称函数

分别是\(y=lnx\)和函数\(y=x-1\)，故得到\(lnx\leq x-1\)。

【法4】：利用代数变换，由\(e^x\ge x+1\)，两边取自然对数得到\(lne^x\ge ln(x+1)\)，

即\(x\ge ln(x+1)\)，再用\(x-1\)替换\(x\)，得到\(x-1\ge lnx\)，即\(lnx\leq x-1\)。

典例剖析

【涉及2017全国卷1理科第11题】设\(x\)，\(y\)，\(z\)为正数，且\(2^x=3^y=5^z\)，则【\(\quad\)】

$A.3y<2x<5z$ $B.2x<3y<5z$ $C.3y<5z<2x$ $D.5z<2x<3y$

分析：令\(2^x=3^y=5^z=k\)，

则\(x=log_2k=\cfrac{lgk}{lg2}\)，\(y=log_3k=\cfrac{lgk}{lg3}\)，\(z=log_5k=\cfrac{lgk}{lg5}\)，

故\(2x=\cfrac{2lgk}{lg2}=\cfrac{lgk}{\cfrac{1}{2}lg2}=\cfrac{lgk}{lg\sqrt{2}}\)，

\(3y=\cfrac{3lgk}{lg3}=\cfrac{lgk}{\cfrac{1}{3}lg3}=\cfrac{lgk}{lg\sqrt[3]{3}}\)，

\(5z=\cfrac{5lgk}{lg5}=\cfrac{lgk}{\cfrac{1}{5}lg5}=\cfrac{lgk}{lg\sqrt[5]{5}}\)，接下来，

法1：【单调性法】转化为只需要比较\(\sqrt[2]{2}\)，\(\sqrt[3]{3}\)，\(\sqrt[5]{5}\)三者的大小即可。

先比较\(\sqrt[2]{2}\)，\(\sqrt[3]{3}\)，给两个式子同时6次方，

得到\((\sqrt[2]{2})^6=2^3=8\)，\((\sqrt[3]{3})^6=3^2=9\)，

故\(\sqrt[2]{2}<\sqrt[3]{3}\)，则\(\cfrac{lgk}{lg\sqrt[2]{2}}>\cfrac{lgk}{lg\sqrt[3]{3}}\)，

即得到\(2x>3y\)

再比较\(\sqrt[2]{2}\)，\(\sqrt[5]{5}\)，给两个式子同时10次方，

得到\((\sqrt[2]{2})^{10}=2^5=32\)，\((\sqrt[5]{5})^{10}=5^2=25\)，

故\(\sqrt[2]{2}>\sqrt[5]{5}\)，则\(\cfrac{lgk}{lg\sqrt[2]{2}}<\cfrac{lgk}{lg\sqrt[3]{3}}\)，

即得到\(5z>2x\)，综上得到\(3y<2x<5z\)

法2：【作差法】

\(2x-3y=\cfrac{2lgt}{lg2}-\cfrac{3lgt}{lg3}=\cfrac{lgt(2lg3-3lg3)}{lg2lg3}=\cfrac{lgt(lg9-lg8)}{lg2lg3}>0\)，

故\(2x>3y\);

\(2x-5z=\cfrac{2lgt}{lg2}-\cfrac{5lgt}{lg5}=\cfrac{lgt(2lg5-5lg2)}{lg2lg5}=\cfrac{lgt(lg25-lg32)}{lg2lg5}<0\)

故\(2x<5z\);

综上有\(3y<2x<5z\)。

法3：【作商法】

\(\cfrac{2x}{3y}=\cfrac{2}{3}\cdot \cfrac{lg3}{lg2}=\cfrac{lg9}{lg8}=log_89>1\)，故\(2x>3y\)；

\(\cfrac{5z}{2x}=\cfrac{5}{2}\cdot \cfrac{lg2}{lg5}=\cfrac{lg2^5}{lg5^2}=log_{25}32>1\)，

故\(5z>2x\)；故\(3y<2x<5z\)。素材链接

法4：【特值法】取\(z=1\)，则由\(2^x=3^y=5^z\)得，\(x=\log_25\)，\(y=\log_35\)，

所以\(2x=\log_25<\log_2{32}=5z\)，

\(3y=\log_3{125}<\log_3{243}=5z\)，所以 \(5z\)最大；

取\(y=1\)，则由\(2^x=3\)，得到\(x=\log_23\)，所以\(2x=\log_29>3y\)，

综上所述，可得\(3y<2x<5z\)，故选\(A\).

法5：设令\(2^x=3^y=5^z=k\)，则\(x=log_2k\)，\(y=log_3k\)，\(z=log_5k\)注意到这三个对数式的真数相同，故想到取倒数，这样得到三个结果的底数就是相同的，便于下一步利用单调性比较大小；，

所以 \(\cfrac{1}{2x}=\log_k{2^{\frac{1}{2}}}\)，\(\cfrac{1}{3y}=\log_k{3^{\frac{1}{3}}}\)，\(\cfrac{1}{5z}=\log_k{5^{\frac{1}{5}}}\)，

又易知，\(k>1\)，则\(5^{\frac{1}{5}}\)\(<\)\(2^{\frac{1}{2}}\)\(<\)\(3^{\frac{1}{3}}\)由于\(5^{\frac{1}{5}}\)\(=\)\(\sqrt[5]{5}\)\(=\)\(\sqrt[10]{5^2}\)，\(2^{\frac{1}{2}}\)\(=\)\(\sqrt[2]{2}\)\(=\)\(\sqrt[10]{2^5}\)，故\(5^{\frac{1}{5}}\)\(<\)\(2^{\frac{1}{2}}\)，同理，\(2^{\frac{1}{2}}\)\(=\)\(\sqrt[2]{2}\)\(=\)\(\sqrt[6]{2^3}\)，\(3^{\frac{1}{3}}\)\(=\)\(\sqrt[3]{3}\)\(=\)\(\sqrt[6]{3^2}\)，故\(2^{\frac{1}{2}}\)\(<\)\(3^{\frac{1}{3}}\)，因此，\(5^{\frac{1}{5}}\)\(<\)\(2^{\frac{1}{2}}\)\(<3^{\frac{1}{3}}\)，

所以，\(\log_k5^{\frac{1}{5}}<\log_k2^{\frac{1}{2}}<\log_k3^{\frac{1}{3}}\)

即\(0<\cfrac{1}{5z}<\cfrac{1}{2x}<\cfrac{1}{3y}\)，

可得\(3y<2x<5z\)，故选\(A\).

已知 \(log_2x=log_3y=log_5z<-1\)，则 【\(\quad\)】

$A.2x < 3y < 5z$ $B.5z < 3y < 2x$ $C.3y < 2x < 5z$ $D.5z < 2x < 3y$

解析：大胆引入第四个变量 \(t\) ，以便于实现变量集中的设想，方便解题；

设 \(t=log_2x=log_3y=log_5z<-1\)，则依次得到，

\(x=2^t\)， \(y=3^t\)， \(z=5^t\)，到此就实现了变量的集中，便于下一步的运算和思考；

则\(2x=2^{t+1}\)， \(3y=3^{t+1}\)， \(5z=5^{t+1}\)，

又由于 \(t<-1\)， 得到\(t+1<0\)，故由幂函数的单调性或者指数函数的图像可知，

\(5^{t+1}<3^{t+1}<2^{t+1}\)，即 \(5z<3y<2x\) ，即选 \(B\).

【2021届高三文科数学】已知 \(1<a<b\)， \(m=a^{b-1}\)， \(n=b^{a-1}\) 则 \(m\)， \(n\) 的大小关系为 【\(\quad\)】

$A.m > n$ $B.m < n$ $C.m = n$ $D.以上选项都有可能$

思路1：如果仅仅是应对考试，可以使用赋值法验证，比如，令\(b=4\)，\(a=2\)，

则\(m=a^{b-1}=2^{4-1}=8\)，\(n=b^{a-1}=4^{2-1}=4\)，则\(m>n\)，故选\(A\)；

思路2：由于比较的是指数式，故我们可能会想到使用作商法，但尝试后发现不行，比如\(\cfrac{m}{n}=\cfrac{a^{b-1}}{b^{a-1}}\)；其原因是没法有效的利用指数函数的性质，但考虑到除法降级运算[用取对数的方法进行降级，由此你也能体会对数运算引入的必要性]对应的是减法，故想到取对数后再比较大小；

法3： 由 \(m=a^{b-1}\)， \(n=b^{a-1}\)， \(1<a<b\)，

得 \(\ln m=(b-1)\ln a\)， \(\ln n=(a-1) \ln b\)，

[若\((b-1)\ln a\) \(>\) \(=\) \(<\) \((a-1)\ln b\)，则可以等价转化为\(\cfrac{\ln a}{a-1}\) \(>\) \(=\) \(<\) \(\cfrac{\ln b}{b-1}\)]

所以要比较 \(m\)， \(n\) 的大小，即比较 \(\cfrac{\ln a}{a-1}\)， \(\cfrac{\ln b}{b-1}\) 的大小，

由于要比较的两个式子结构相同，故想到构造函数法，设 \(f(x)=\cfrac{\ln x}{x-1}(x>1)\)此处可以利用导数探究其单调性，也可以利用幂函数\(y=x-1\)和对数函数\(y=\ln x\)的增长速度的不同来粗浅的判断；函数与导数中常用的函数和不等关系\(\quad\)，

则 \(f'(x)=\cfrac{\frac{x-1}{x}-\ln x}{(x-1)^{2}}=\cfrac{x-1-x\ln x}{x(x-1)^{2}}\)，

设 \(g(x)=x-1-x\ln x\)，则 \(g^{\prime}(x)=1-\ln x-1=-\ln x\)，

当 \(x>1\) 时, \(g^{\prime}(x)<0\) ，所以 \(g(x)<g(1)=0\)，

即 \(f^{\prime}(x)<0\)， 所以 \(f(x)\) 为 \((1,+\infty)\) 上的减函数.

因为 \(1<a<b\)， 所以 \(f(a)>f(b)\)，即 \(\cfrac{\ln a}{a-1}>\cfrac{\ln b}{b-1}\)，

\((b-1)\ln a>(a-1)\ln b\)， \(\ln m>\ln n\)， 从而 \(m>n\)， 故选 \(A\).

【2021届宝鸡市一检文科数学第12题】 直线 \(y=ax+c\) 与曲线 \(y=e^{x}\) 相切于点 \((x_{0}, e^{x_{0}})\) ，且 \(x_{0}\in[0,1]\)，设 \(b=\log _{5}(3^{a}+4^{a})\)， 则 \(a\) 与 \(b\) 的大小关系是 【\(\quad\)】

$A.a=b$ $B.a > b$ $C.a < b$ $D.以上均有可能$

解析：由直线 \(y=ax+c\) 与曲线 \(y=e^{x}\) 相切于点 \((x_{0}, e^{x_{0}})\)可知 ，则切线斜率为 \(k=a\) 且 \(k=e^{x_0}\)，

则\(a=e^{x_0}\)，又由于\(x_{0}\in[0,1]\)，故\(a\in [1,e]\)，问题转换为：

当 \(a\in [1,e]\) 时，比较 \(b=\log _{5}(3^{a}+4^{a})\) 与 \(a\)的大小关系；

注意到 \(b\) 为对数式，故想到将 \(a\) 对数化为 \(a=log_55^a\)，

比较\(b=\log _{5}(3^{a}+4^{a})\) 与 \(a=log_55^a\) 的大小，这样只需要比较 \(3^a+4^a\) 与 \(5^a\) 的大小关系，

注意到，\(3^2+4^2=5^2\)，我们想到需要针对 \(a\) 分类讨论，可以使用验证法；

当\(a=1\)时，\(3^1+4^1>5^1\)，故\(b>a\)；

当\(a=2\)时，\(3^2+4^2=5^2\)，故\(b=a\)；

当\(a=\cfrac{5}{2}\)时，\(3^{\frac{5}{2}}+4^{\frac{5}{2}}\approx48.2\)，\(5^{\frac{5}{2}}=25\sqrt{5}\approx57.5\)，故\(b<a\)；

故选\(D\)；

补充：①\(7\leqslant 3^a+4^a\leqslant 3^e+4^e\)，\(5\leqslant 5^a\leqslant 5^e\)；

②\(\cfrac{3^a+4^a}{5^a}=(\cfrac{3}{5})^a+(\cfrac{4}{5})^a\)； \(\cos\theta\)，\(\sin\theta\)；

③证明，若\(3^n+4^n>5^n\)，则\(n>2\)；

【2021届宝鸡市一检理科数学第12题】 设 \(1<a<2\)， \(m=\log _{4}(2^{a}+3^{a})\)， \(n=\log _{5}(3^{m}+4^{m})\)， 则 【\(\quad\)】

$A.n=2$ $B.n >2$ $C.n <2$ $D.以上均有可能$

法1： 不等式性质法，因为 \(1<a<2\)， 所以 \(5<2^{a}+3^{a}<13\)，

所以 \(1<\log_{4}5<m<\log_{4}13<2\)，

所以 \(1<m<2\)， 所以 \(7<3^{m}+4^{m}<25\)，

所以 \(1<\log _{5}7<n<\log _{5}25=2\)

所以 \(n<2\)， 故选 \(C\) .

法2：估值计算法，

令\(a=\cfrac{3}{2}\)，\(2^{\frac{3}{2}}+3^{\frac{3}{2}}=2\sqrt{2}+3\sqrt{2}=5\sqrt{2}=\sqrt{50}=7\)

\(m=log_47\approx log_48=\cfrac{3}{2}log_22=\cfrac{3}{2}\)；

当\(m=\cfrac{3}{2}\)时，\(3^{\frac{3}{2}}+4^{\frac{3}{2}}\approx 13.2\)，

\(n=\log _{5}(3^{m}+4^{m})=\log_513.2<\log_5 25=2\)，故\(n<2\)，故选 \(C\) ；

【2020全国卷Ⅲ文】设\(a=\log_32\)，\(b=\log_53\)，\(c=\cfrac{2}{3}\)，则【\(\quad\)】

$A.a< c < b$ $B.a< b < c$ $C.b< c < a$ $D.c< a < b$

法1：由于\(2^3<3^2\)，两边同时\(\cfrac{1}{3}\)次方，即\(2<3^{\frac{2}{3}}\)，

两边同时取以\(3\)为底数的对数，得到\(\log_32<\log_33^{\frac{2}{3}}=\cfrac{2}{3}\)，

即\(\log_32<\cfrac{2}{3}\)，则\(a<c\)；

又由于\(3^3>5^2\)，两边同时\(\cfrac{1}{3}\)次方，即\(3>5^{\frac{2}{3}}\)，

两边同时取以\(5\)为底数的对数，得到\(\log_53>\log_55^{\frac{2}{3}}=\cfrac{2}{3}\)，

即\(\log_53>\cfrac{2}{3}\)，则\(b>c\)；

综上所述，得到 \(a<c<b\)，故选 \(A\).

法2：作商法，由于\(a,b,c>0\)，故尝试采用作商法，

\(\cfrac{a}{c}\)\(=\)\(\cfrac{\log_32}{\frac{2}{3}}\)\(=\)\(\cfrac{3}{2}\log_32\)\(=\)\(\log_32^{\frac{3}{2}}\)\(=\)\(\log_3\sqrt{8}\)\(=\)\(\log_{\sqrt{9}}{\sqrt{8}}\)\(<\)\(1\)，故\(a<c\)；

\(\cfrac{b}{c}\)\(=\)\(\cfrac{\log_53}{\frac{2}{3}}\)\(=\)\(\cfrac{3}{2}\log_53\)\(=\)\(\log_53^{\frac{3}{2}}\)\(=\)\(\log_5\sqrt{27}\)\(=\)\(\log_{\sqrt{25}}{\sqrt{27}}\)\(>\)\(1\)，故\(b>c\)；

综上所述，得到 \(a<c<b\)，故选 \(A\).

【2020全国卷Ⅲ理】已知\(5^5<8^4\)，\(13^4<8^5\)，设\(a=\log_53\)，\(b=\log_85\)，\(b=\log_{13}8\)，，则【\(\quad\)】

$A.a< b < c$ $B.b< a < c$ $C.b< c < a$ $D.c< a < b$

解析：\(\cfrac{a}{b}\)\(=\)\(\cfrac{\log_53}{\log_85}\)\(=\)\(\log_53\cdot\log_58\)

\(<\)\(\bigg(\cfrac{\log_53+\log_58}{2}\bigg)^2\)\(=\)\(\bigg(\cfrac{\log_5{24}}{2}\bigg)^2\)\(<\)\((\cfrac{\log_5{25}}{2})^2\)\(=\)\(1\)，故\(\log_53<\log_{8}5\)；

由于\(5^5<8^4\)，\(13^4<8^5\)，给两式分别取以\(8\)和\(13\)为底的对数，

\(5\log_85<4\log_88=4\)，\(4=4\log_{13}{13}<5\log_{13}8\)，即\(5\log_85<5\log_{13}8\)，

即\(\log_85<\log_{13}8\)，则 \(\log_53<\log_{8}5<\log_{13}8\)，即\(a<b<c\)，故选\(A\).

补充思路：二分法思想，我们可以确定 \(a=\log_53\in (\cfrac{1}{2},1)\)， \(b=\log_85\in (\cfrac{1}{2},1)\)，此时如果要进一步比较，可以考虑中间量选为区间中点 \(\cfrac{3}{4}\)，

比如要确定 \(\log_53\) 的范围，即比较 \(\log_53\) 与 \(\cfrac{3}{4}\) 的大小，即 比较 \(\log_53\) 与 \(\log_55^{\frac{3}{4}}\) 的大小，

即比较 \(3\) 与 \(5^{\cfrac{3}{4}}\) 的大小，即比较 \(3^{\cfrac{4}{4}}\) 与 \(5^{\cfrac{3}{4}}\) 的大小，

此时， \(3^{\cfrac{4}{4}}=\sqrt[4]{3^4}\)，\(5^{\cfrac{3}{4}}=\sqrt[4]{5^3}\)，\(3^4<5^3\)，

故 \(\log_53<\cfrac{3}{4}\) ，即 \(\log_53\in (\cfrac{1}{2},\cfrac{3}{4})\)，

同理，可得 \(\log_85\in (\cfrac{3}{4},1)\)，故 \(\log_53<log_85\)；

【2005 \(\cdot\) 湖北高考】已知\(x\in(0,\cfrac{\pi}{2})\)，则 \(2x\) 与 \(3\sin x\) 的大小关系是 【\(\qquad\)】

$A.2x >3\sin x$ $B.2x <3\sin x$ $C.2x=3\sin x$ $D.与 x的取值有关$

解：令 \(g(x)=2x-3\sin x\)，则 \(g'(x)=2-3\cos x\)，令 \(g'(x)=0\) ，得到 \(x=\arccos\cfrac{2}{3}\)，

则当 \(0<x<\arccos\cfrac{2}{3}\)，\(g'(x)<0\)，\(g(x)\) 单调递减，\(g(x)<g(0)=0\)，\(2x<3\sin x\)；

当 \(\arccos\cfrac{2}{3}<x<\cfrac{\pi}{2}\) 时， \(g'(x)>0\)，\(g(x)\) 单调递增，

但是 \(g(\arccos\cfrac{2}{3})<0\)，\(g(\cfrac{\pi}{2})>0\)，

所以在区间 \([\arccos\cfrac{2}{3},\cfrac{\pi}{2})\) 内必有且仅有一点 \(\theta\) 使得 \(g(\theta)=0\)，

当 \(\arccos\cfrac{2}{3}\leq x<\cfrac{\pi}{2}\) 时， \(g(x)<g(\theta)=0\)， 则\(2x<3\sin x\)；

当 \(\theta< x<\cfrac{\pi}{2}\) 时， \(g(x)>g(\theta)=0\)， 则\(2x>3\sin x\)；

综上所述，当 \(0<x<\theta\) 时， \(2x<3\sin x\)，

当 \(x=\theta\) 时， \(2x=3\sin x\)，

当 \(\theta< x<\cfrac{\pi}{2}\) 时， \(2x>3\sin x\)；

故选 \(D\) .

解后反思：本题目若不采用反三角函数，则可以考虑 特殊值法。

【2024高三数学演练】已知 \(a=\cfrac{5}{6}\ln\cfrac{6}{7}\)， \(b=\cfrac{6}{7}\ln\cfrac{5}{6}\)， \(c=-\cfrac{5}{42}\)，则【\(\qquad\)】

$A.a< b < c$ $B.b< a < c$ $C.b< c < a$ $D.c< a < b$

解：由糖水定律可知，\(\cfrac{5}{6}<\cfrac{5+1}{6+1}=\cfrac{6}{7}\)，又指数函数 \(y=(\cfrac{6}{7})^x\) 单调递减，故 \((\cfrac{6}{7})^\cfrac{5}{6}>(\cfrac{6}{7})^\cfrac{6}{7}\)；

又幂函数 \(y=x^{\cfrac{6}{7}}\) 单调递增，故 \((\cfrac{6}{7})^\cfrac{6}{7}>(\cfrac{6}{7})^\cfrac{5}{6}\)；则有 \((\cfrac{6}{7})^\cfrac{5}{6}>(\cfrac{5}{6})^\cfrac{6}{7}\)；

两边同时取自然对数，得到 \(\cfrac{5}{6}\ln\cfrac{6}{7}>\)\(\cfrac{6}{7}\ln\cfrac{5}{6}\)，即 \(a>b\)，

又由于 \(\cfrac{a}{c}=\cfrac{\cfrac{5}{6}\ln\cfrac{6}{7}}{-\cfrac{5}{42}}=-7\ln\cfrac{6}{7}=\ln(\cfrac{6}{7})^{-7}=\ln(\cfrac{7}{6})^{7}>\ln e=1\)，

又由于 \(c<0\)，故给 \(\cfrac{a}{c}>1\) 两边同时乘以 \(c\)，得到 \(a<c\)，故 \(c>a>b\)，选 \(B\) .

---

1. 作差法步骤：作差 \(\rightarrow\) 变形 \(\rightarrow\) 定号 \(\rightarrow\) 结论，其难点是数学变形，常用的数学变形有因式分解，配方法，通分，分子分母有理化等，有时候针对根式作差时，可能会需要先平方再作差。 ↩︎