函数图像习题
前言
典例剖析
分析:函数\(y=f(2x-1)\)图像到函数\(y=f(2x+1)\)的图像的变换只涉及左右平移变换,而左右平移变换的本质即用\(x+\phi\)替换单独的自变量\(x\)整理得到的,
故用\(x+\phi\)替换\(y=f(2x-1)\)中的单独的自变量\(x\),整理得到\(f(2(x+\phi)-1)=f(2x+1)\),由\(2(x+\phi)-1=2x+1\)解得\(\phi=1\),
即上述替换是用\(x+1\)替换\(x\)得到的,故由左加右减的口诀得到,
应该将函数\(y=f(2x-1)\)向左平移\(1\)个单位,得到函数\(y=f(2x+1)\),
而\(y=f(2x-1)\)的对称轴是\(x=0\)[\(y\)轴],故函数\(y=f(2x+1)\)的对称轴为\(x=-1\)。故选\(A\)。
(1)求\(f(x)\)的解析式;
分析:设\(f(x)\)图像上任一点\(P(x,y)\),
则点\(P\)关于\((0,1)\)点的对称点\(P'(-x,2-y)\)必在\(h(x)\)的图像上,
即\(2-y=-x-\cfrac{1}{x}+2\),
即\(y=f(x)=x+\cfrac{1}{x}(x\neq 0)\)。
(2)若\(g(x)=f(x)+\cfrac{a}{x}\),且\(g(x)\)在区间\((0,2]\)上为减函数,求实数\(a\)的取值范围。
分析:\(g(x)=f(x)+\cfrac{a}{x}=x+\cfrac{a+1}{x}\),
则\(g'(x)=1-\cfrac{a+1}{x^2}\),
由于\(g(x)\)在区间\((0,2]\)上为减函数,
则\(g'(x)=1-\cfrac{a+1}{x^2}\leq 0\)在区间\((0,2]\)上恒成立,
即\(a+1\ge x^2\)在区间\((0,2]\)上恒成立,
则\(a+1\ge 4\),即\(a\ge 3\),
故实数\(a\)的取值范围为\([3,+\infty)\)。
分析:函数\(y=2f^2(x)-3f(x)+1\)的零点个数即方程\(2f^2(x)-3f(x)+1=0\)的根的个数,
故先求解方程\(2f^2(x)-3f(x)+1=0\),即\([2f(x)-1][f(x)-1]=0\),
解得\(f(x)=1\)或\(f(x)=\cfrac{1}{2}\),
接下来原方程的根的个数转化为方程\(f(x)=1\)或\(f(x)=\cfrac{1}{2}\)的根的个数,
故做出函数\(y=f(x)\)的图像和直线\(y=1\)和\(y=\cfrac{1}{2}\),
由图像可以看出,其共有\(5\)个交点,故原函数的零点个数为\(5\)个。
已知函数\(f(x)=x^2-|x|+a\)与\(y=1\)有\(4\)个交点,则实数\(a\)的取值范围是_______________。
分析:将函数转化为\(f(x)=|x|^2-|x|+a\),故\(f(x)\)为偶函数,
重点做\(x\ge 0\)时的函数图像,\(f(x)=x^2-x+a=(x-\cfrac{1}{2})^2+a-\cfrac{1}{4}(x\ge 0)\),
对称轴为\(x=\cfrac{1}{2}\),最低点为\((\cfrac{1}{2},a-\cfrac{1}{4})\),和\(y\)轴的交点为\((0 ,a)\),
再完善\(x<0\)时的图像,得到函数\(y=f(x)\)的完整图像,
想一想,当参数\(a\)变化时,\(f(x)\)的图像如何变化?
由图像可知,要使得函数\(f(x)=x^2-|x|+a\)与\(y=1\)有\(4\)个交点,
则必须满足\(a>1\)且\(a-\cfrac{1}{4}<1\),
解得\(a\in (1,\cfrac{5}{4})\)。
分析:由下图可知,函数\(f(x)\)经过\((0,0)\),故有\(f(0)=0\),则\(m\neq 0\)
又由于定义域为\(R\),故分母\(x^2+m>0\)恒成立,即\(m>0\),
[说明:此时不会有\(m<0\),否则定义域不会是\(R\),比如分母为\(x^2-4\),则定义域中不会有\(x=-2\)和\(x=2\)这两个点]
又由图像可知,\(x>0\)时,则\(f(x)>0\),即\(f(x)=\cfrac{(2-m)x}{x^2+m}>0\),
故\(2-m>0\),解得\(m<2\);
同时,由图像还可以看出,\(f(x)\)在区间\([-1,1]\)上单调递增,\(x=-1\)和\(x=1\)分别是其最小值点和最大值点。
故\(f'(x)\ge 0\)在区间\([-1,1]\)上恒成立,
即\(f'(x)=\cfrac{(2-m)(x^2+m)-(2-m)\cdot x \cdot 2x}{(x^2+m)^2}\)
\(=\cfrac{(2-m)(m-x^2)}{(x^2+m)^2}\ge 0\)在区间\([-1,1]\)上恒成立,
由于\(2-m>0\),故\(m-x^2\ge 0\)在区间\([-1,1]\)上恒成立,
故\(m\ge 1\),有\(m<2\),
即\(m\)的取值范围是\([1,2)\)。
【变式题】图像变化为下图后,则则\(m\)的取值范围是______________。
分析:此时图像的变化为,\(x=\pm 1\)不再是最值点,但是函数还是在区间\([-1,1]\)上单调递增;求解如下,
由上也可以知道先\(m>0\)且\(m<2\),
由于函数在区间\([-1,1]\)上单调递增;但是\([-1,1]\)只是其单调递增区间的子区间,不包含最值点,
故只能得到\(f'(x)>0\)在区间\([-1,1]\)上恒成立,
故解得\(m>1\),即\(m\)的取值范围是\((1,2)\)。
补充解法:或者\(f(x)=\cfrac{(2-m)x}{x^2+m}=\cfrac{2-m}{x+\frac{m}{x}}\),由于\(f(x)\)在\((0,\sqrt{m})\)上单调递增,在\((\sqrt{m},+\infty)\)上单调递减,所以\(\sqrt{m}>1\),得到\(m>1\);
分析:\(f(x)=\cfrac{2^x|cos2x|}{2^{2x}-1}=\cfrac{|cos2x|}{2^x-2^{-x}}\),
由于其组成部分\(y=2^x-2^{-x}\)为奇函数,\(y=|cos2x|\)为偶函数,
故函数\(f(x)\)为奇函数。
法1:从形的角度入手分析,在同一个坐标系中做出静态函数\(y=|f(x)|\)的图像和动态函数\(y=ax\)的图像,然后让动态函数的斜率\(a\)变化,就可以发现,
当\(k\leq a\leq 0\)时满足\(|f(x)|\ge ax\),
其中\(k\)是函数\(y=ax\)与函数\(y=x^2-2x\)在点\((0,0)\)处的切线的斜率。
由\(y=h(x)=x^2-2x\)得到,\(h'(x)=2x-2\),则\(h'(0)=k=-2\),
故\(-2\leq a\leq 0\),故选\(D\)。
[补充说明]为什么会相切于点\((0,0)\),还可以这样解释;
由\(y=x^2-2x(x\leqslant 0)\)和\(y=ax(x\leqslant 0)\)联立,得到\(x^2-(a+2)x=0\),由于二者相切,
故由\(\Delta=(a+2)^2=0\),得到\(a=-2\),代入上述方程\(x^2-(a+2)x=0\),得到\(x=0\),且\(y=0\),
即当直线\(y=ax\)的斜率\(a=-2\)时,与曲线\(y=x^2-2x(x\leqslant 0)\)相切于点\((0,0)\);
法2:从数的角度入手分析,
(1).当\(x>0\)时,要使得\(|f(x)|\geqslant ax-1\),即\(|\ln(x+1)|=\ln(x+1)\geqslant ax\),显然需要\(a\leqslant 0\);
(2).当\(x\leqslant 0\)时,要使得\(|f(x)|\geqslant ax\),即\(|-x^2+2x|=x^2-2x\geqslant ax\),即\(ax\leqslant x^2-2x\)恒成立,
当①\(x=0\)时,即\(a\in R\)时满足题意;
②\(x<0\)时,即\(a\geqslant x-2\)恒成立,又由于\(x-2<-2\)即\(x-2\)在\(x<0\)时的最大值的极限为\(-2\)\(\quad\),则\(a\geqslant -2\);
故当\(x\leqslant 0\)时,需要\(a\geqslant -2\),
综上所述,得到\(-2\leqslant a\leqslant 0\),故选\(D\).

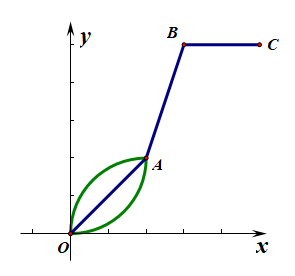
- 第4题,当杯中水的高度\(h\)沿着线段\(OA\)增长时,由于线段\(OA\)的斜率是固定不变的,故容器必然会是上下大小一致的,
当杯中水的高度\(h\)沿着上凸形曲线\(OA\)增长时,由于上凸形曲段\(OA\)的斜率是由大到小变化的,故容器必然会是上大下小形的,
当杯中水的高度\(h\)沿着下凹形曲线\(OA\)增长时,由于下凹形曲线\(OA\)的斜率是由小到大变化的,故容器必然会是下大上小形的,



备忘,以后补充:四个几何体,同底等高,圆柱体,正立三棱锥,倒立三棱锥,球体,
匀速向其内部注水,其体积是水面高度的函数图像,
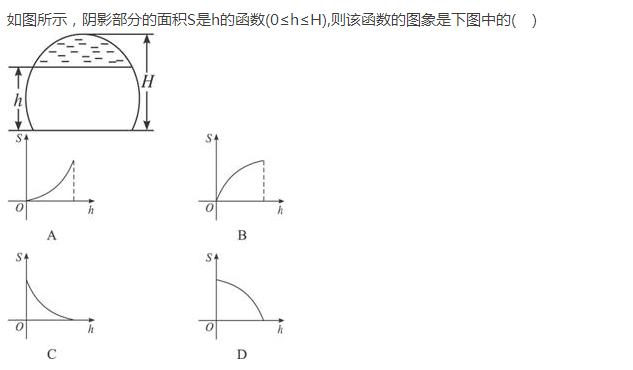
四个平面几何图形,同底等高,圆柱,正立三角形,倒立三角形,圆,
匀速向其内部注水,其面积是水面高度的函数图像,
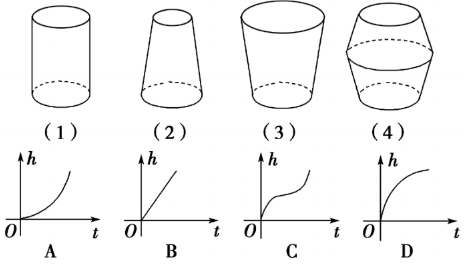
解:(1)→(B),(2)→(A),(3)→(D),(4)→(C)
【规律总结】 若函数在某范围内导数的绝对值较大,则函数在这个范围内“增”或“减”得快,
函数的图象比较“陡峭”,反之,函数的图象“平缓”。
分析:由于周期为\(3\),故先做半周期\([0,\cfrac{3}{2})\)上的函数图像,\(f(0)=0\),\(f(x)=ln[(x-\cfrac{1}{2})^2+\cfrac{3}{4}]\),
故\(x\in (0,\cfrac{1}{2})\)单调递减,且\(f(\cfrac{1}{2})<0\),\(x\in (\cfrac{1}{2},\cfrac{3}{2})\)上单调递增,
但是由于\(f(x)\)是奇函数,且有周期性,故只能\(f(\cfrac{3}{2})=0\),
故做出\(x\in [0,\cfrac{3}{2}]\)上的函数图像,在利用奇偶性做出\(x\in [-\cfrac{3}{2},0]\)上的函数图像,
再平移得到函数\(f(x)\),\(x\in[0,6]\)上的函数图像,如下图所示,
由图可知,函数\(f(x)\)在区间\([0,6]\)上的零点个数是\(9\)个。
零点分别为\(x=0\),\(x=1\),\(x=\cfrac{3}{2}\),\(x=2\),\(x=3\),\(x=4\),\(x=\cfrac{9}{2}\),\(x=5\),\(x=6\)。
分析:这类题目总的解决途径无非是从形的角度和从数的角度两个方面思考:
法1:从形的角度,自然需要我们对常见函数的图像以及所含参数\(m\)的含义要非常清楚才行。
注意到两个函数图像都会随着参数\(m\)的取值变化而变化,都是动图。
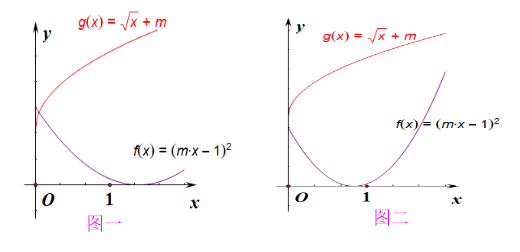
第一种情形,如图一所示,二者在对称轴\(x=\cfrac{1}{m}\)的左侧只有一个交点,右侧不能有交点
则有\(\begin{cases}f(0)\ge g(0)\\ f(1)<g(1)\end{cases}\),即\(\begin{cases}1\ge m\\ (m-1)^2<m+1\end{cases}\),
解得,\(0<m\leq 1\);
第二种情形,如图二所示,二者在对称轴\(x=\cfrac{1}{m}\)的左侧没有交点,右侧只有一个交点
则有\(\begin{cases}f(0)< g(0)\\ f(1)\ge g(1) \end{cases}\),即\(\begin{cases}1< m\\ (m-1)^2\ge m+1 \end{cases}\),
解得,\(m\ge 3\);
综上所述,\(m\)的取值范围为\((0,1]\cup[3,+\infty)\) ,选B.
分析:本题目要求将源函数\(y=cos(2x-\cfrac{\pi}{3})\),变换得到目标函数\(y=sin(2x+\cfrac{\pi}{3})\),为此,我们需要先将二者的函数名称做统一;
法1:源函数\(y=cos(2x-\cfrac{\pi}{3})=sin(\cfrac{\pi}{2}-2x+\cfrac{\pi}{3})=sin(-2x+\cfrac{5\pi}{6})\),这种变换要得到目标函数\(y=sin(2x+\cfrac{\pi}{3})\),不仅仅是左右平移;故需要调整使用的公式;
源函数\(y=cos(2x-\cfrac{\pi}{3})=sin(\cfrac{\pi}{2}+2x-\cfrac{\pi}{3})=sin(2x+\cfrac{\pi}{6})\),用替换法,由\(2(x+\phi)+\cfrac{\pi}{6}=2x+\cfrac{\pi}{3}\),得到\(\phi=\cfrac{\pi}{12}\),即使用\(x+\cfrac{\pi}{12}\)替换单独的自变量\(x\)后得到目标函数,故需要向左平移\(\cfrac{\pi}{12}\),则选\(A\);
法2:将目标函数\(y=sin(2x+\cfrac{\pi}{3})\)变换为余弦函数,略;

 总结函数图像中的有价值题目。
总结函数图像中的有价值题目。

 浙公网安备 33010602011771号
浙公网安备 33010602011771号