2019届[月考01-03]高三理科数学试题参考答案
【01】第一次月考
考试试卷,已上传,暂时隐藏
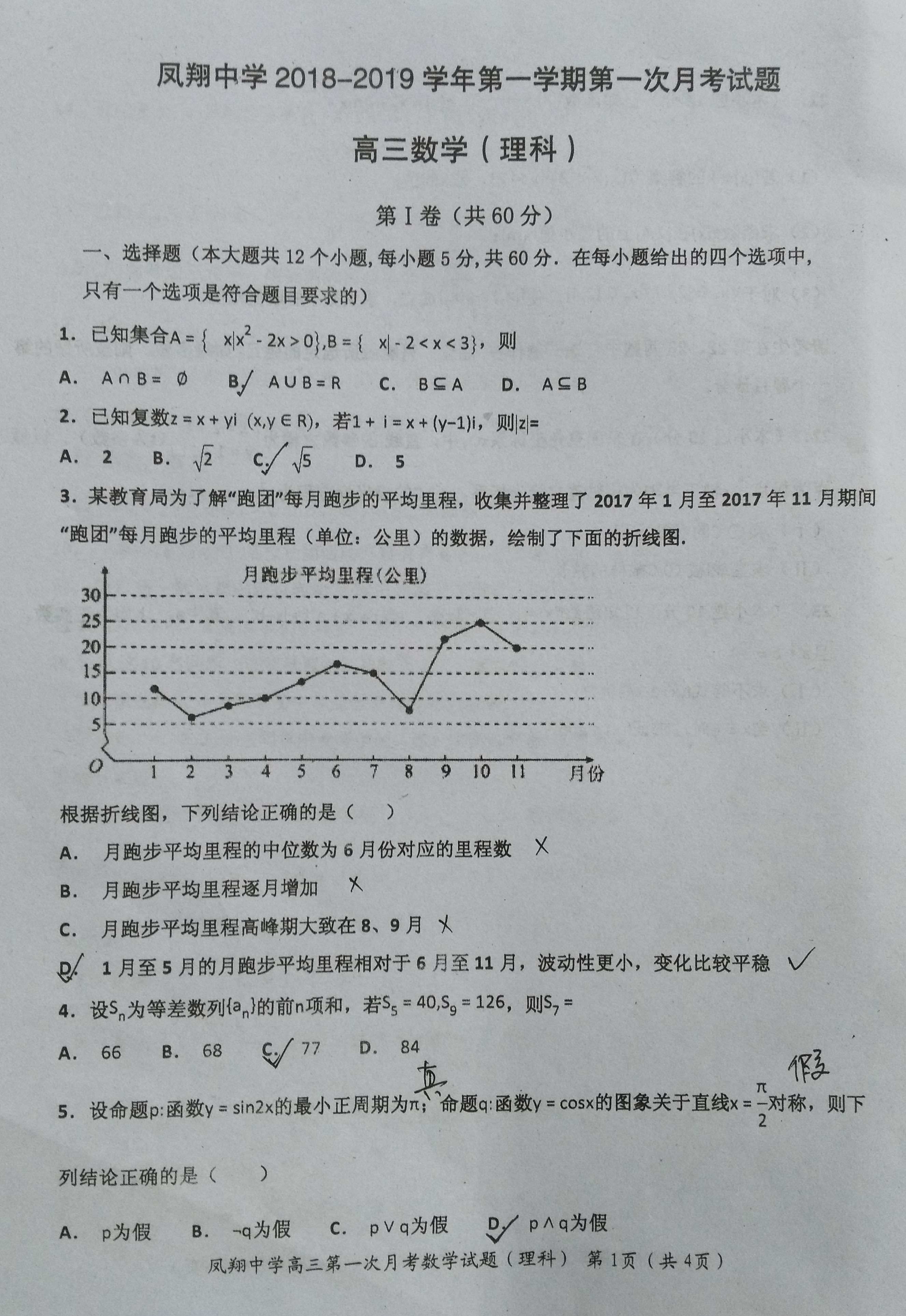



- 2、具体的解析图片,已上传,暂时隐藏;个别典型题目有时间再编辑;
- 3、学科组提供的参考答案:




【02】第二次月考
考试试卷,已上传,暂时隐藏




- 月考二学科组提供的参考答案:




【2019高三理科数学第二次月考第16题】
在平行四边形\(ABCD\)中,点\(M\)在边\(CD\)上,且满足\(DM=\cfrac{1}{3}DC\),点\(N\)在\(CB\)的延长线上,且满足\(CB=BN\),若\(AB=3\),\(AD=4\),则\(\overrightarrow{AM}\cdot \overrightarrow{NM}\)的值为__________。
分析:我们一般做出的平行四边形是\(\angle BAD\neq 90^{\circ}\)的,从形上思考求向量的内积时几乎没有思路,
此时我们不妨思考,能不能建立直角坐标系,引入点的坐标,然后利用坐标运算内积。这是一个突破;由形到数的思维转化;
其次,观察你做出来的平行四边形,当边\(AD\)绕着点\(A\)逆时针旋转时,我们仍可以保证边\(AB\)和\(AD\)的长度不变化,
那么此时自然就会想起来“特殊化策略”,这是思维上的第二个突破;
【特殊化策略】将平行四边形\(ABCD\)直接特殊化为矩形,以点\(A\)为原点,分别以\(AB、AD\)所在直线为\(x\)轴和\(y\)轴,建立平面直角坐标系,
则点\(A(0,0)\),点\(M(1,4)\),点\(N(3,-4)\),则\(\overrightarrow{AM}=(1,4)\),\(\overrightarrow{NM}=(-2,8)\),
则\(\overrightarrow{AM}\cdot \overrightarrow{NM}=(1,4)\cdot (-2,8)=-2+32=30\)。
【2019高三理科数学第二次月考第21题】
已知函数\(f(x)=alnx-x+1\),
(1)若\(f(x)\)的图像在\(x=1\)处的切线\(l\)在\(y\)轴上的截距为\(-1\),求\(a\)的值及直线\(l\)的方程。
分析:函数\(f(x)=alnx-x+1\),则\(f'(x)=\cfrac{a}{x}-1\),
则\(k=f'(1)=a-1\),又知切点为\((1,0)\),
则切线\(l\)方程为\(y-0=(a-1)(x-1)\),
由切线\(l\)在\(y\)轴上的截距为\(-1\),令\(x=0\),解得\(a=2\),
故切线\(l\)方程为\(y=x-1\),即\(x-y-1=0\)。
(2)若函数\(f(x)\)的图像上存在不同的两点\(A(x_1,y_1)\)、\(B(x_2,y_2)\),使得直线\(AB\)的斜率\(k\ge \cfrac{4}{x_1x_2}\),求实数\(m\)的取值范围。
分析:转化为能成立,求导,再检验即可。
若函数\(f(x)\)的图像上存在不同的两点\(A(x_1,y_1)\)、\(B(x_2,y_2)\),
使得直线\(AB\)的斜率\(k\ge \cfrac{4}{x_1x_2}\),则必有\(\cfrac{f(x_2)-f(x_1)}{x_2-x_1}\ge \cfrac{4}{x_1x_2}\)成立,
不妨设\(0<x_1<x_2\),则上式等价变形为\(f(x_2)-f(x_1)\ge \cfrac{4(x_2-x_1)}{x_1x_2}\),
即\(f(x_2)-f(x_1)\ge 4(\cfrac{1}{x_1}-\cfrac{1}{x_2})\)能成立,
即\(f(x_2)+\cfrac{4}{x_2}\ge f(x_1)+\cfrac{4}{x_1}\),
令\(g(x)=f(x)+\cfrac{4}{x}\),则有\(g(x_2)\ge g(x_1)\)能成立,
即函数\(g(x)\)在区间\((0,+\infty)\)上为常函数或增函数能成立。
即\(g'(x)\ge 0\)在区间\((0,+\infty)\)上能成立,
则\(\cfrac{a}{x}-1-\cfrac{4}{x^2}\ge 0\)在区间\((0,+\infty)\)上能成立,
则\(a\ge x+\cfrac{4}{x}\)在区间\((0,+\infty)\)上能成立,
而\([x+\cfrac{4}{x}]_{min}=4\),当且仅当\(x=2\)时取得等号。
故\(a\ge 4\),接下来需要验证\(a=4\)时是否满足题意。
当\(a=4\)时,函数\(g(x)=4lnx-x+1+\cfrac{4}{x}\),
\(g'(x)=\cfrac{4}{x}-1-\cfrac{4}{x^2}=\cfrac{-(x-2)^2}{x^2}\),
由\(g'(x)\leq 0\)可知,\(a=4\)时不满足题意,舍去,
故\(a\)的取值范围是\(a\in (4,+\infty)\)。
【解后反思】①利用单调性求参数的取值范围时,常常转化为恒成立或能成立问题,得到的不等式往往是带有等号的,此时可能会多解,故需要检验;
②一般的检验我们是将其代入函数中,观察其只要不是常函数,就保留,若是常函数,则舍弃;
③其实上述的观察法还是有些肤浅,尤其是函数比较特殊时,更显得这个方法不太可靠,比如本题目。
④注意本题目转化中的构造函数的技巧;
⑤本题目的这种解法有些不通顺的地方是:函数只要有单增区间就可以。
【2019高三理科数学第二次月考第11题】
函数\(f(x)=\left\{\begin{array}{l}{log_2(x+2), x\leq 0}\\{f(x-1),x>0}\end{array}\right.\),则方程\(f(x)-\cfrac{1}{3}x=0\)的根的个数为【3】个。
故由图可知,函数\(y=f(x)\)与\(y=\cfrac{1}{3}x\)的图像交点有\(3\)个。
故方程\(f(x)-\cfrac{1}{3}x=0\)的根的个数为【3】个。
【2019高三理科数学第二次月考第9题】【函数性质的综合应用】
函数\(f(x)=ln(|x|-1)-log_{0.5}(x^2+1)\),则使得不等式\(f(x)-f(2x-1)<0\)成立的\(x\)的取值范围是【】
\(A、(1,+\infty)\);\(B、(-\infty,-\cfrac{1}{3})\);\(C、(-\infty,-\cfrac{1}{3})\cup (1,+\infty)\);\(D、(-\infty,-1)\cup (1,+\infty)\);
分析:由\(|x|-1>0\)得到定义域\((-\infty,-1)\cup (1,+\infty)\);
由于\(y=ln(|x|-1)\)为偶函数,\(y=-log_{0.5}(x^2+1)\)为偶函数,【两个组成部分】
所以\(f(x)\)为偶函数;【整体】
以下主要讨论单调性,先考虑\(x>1\)的情形,
由于\(x>1\)时\(f(x)=ln(x-1)-log_{0.5}(x^2+1)\),
其中\(y=ln(x-1)\)在区间\((1,+\infty)\)上单调递增,\(y=log_{0.5}(x^2+1)\)在区间\((1,+\infty)\)上单调递增,
故\(f(x)=ln(x-1)-log_{0.5}(x^2+1)\)区间\((1,+\infty)\)上单调递增,
又由于其为偶函数,这样可知\((-\infty,-1)\)上单调递减,
由不等式\(f(x)-f(2x-1)<0\)等价于\(f(|x|)<f(|2x-1|)\),
其在区间\((1,+\infty)\)上单调递增,
由定义域和单调性二者限制得到,
\(\left\{\begin{array}{l}{|x|>1}\\{|2x-1|>1}\\{|x|<|2x-1|}\end{array}\right.\)
上式等价于\(\left\{\begin{array}{l}{|x|>1①}\\{|x|<|2x-1|②}\end{array}\right.\)
解①得到,\(x<-1\)或\(x>1\);
解②,两边同时平方,去掉绝对值符号,得到\(x<-\cfrac{1}{3}\)或\(x>1\);
二者求交集得到,\(x<-1\)或\(x>1\),故选D。
【03】第一次月考
- 试题图片


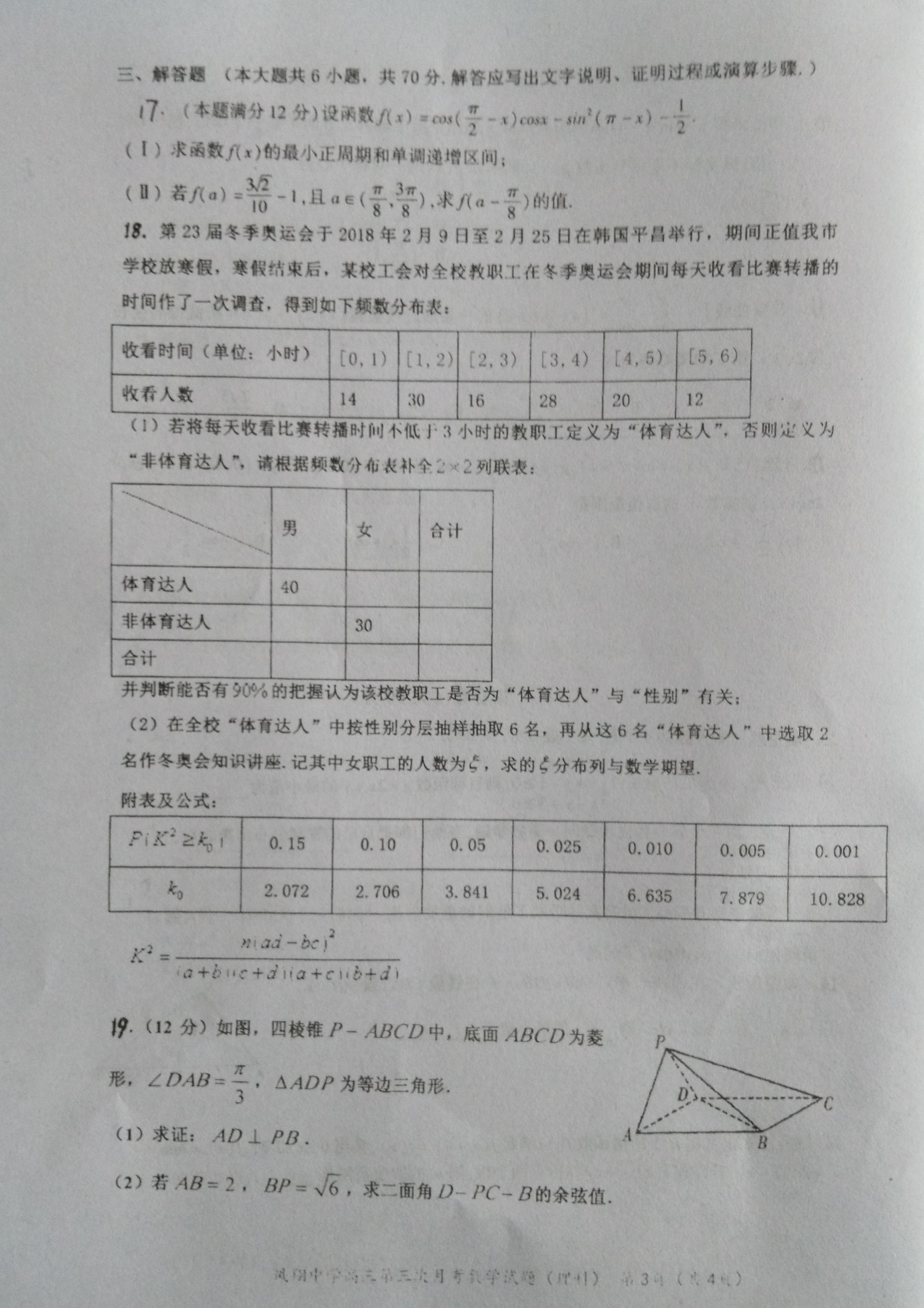

- 参考答案
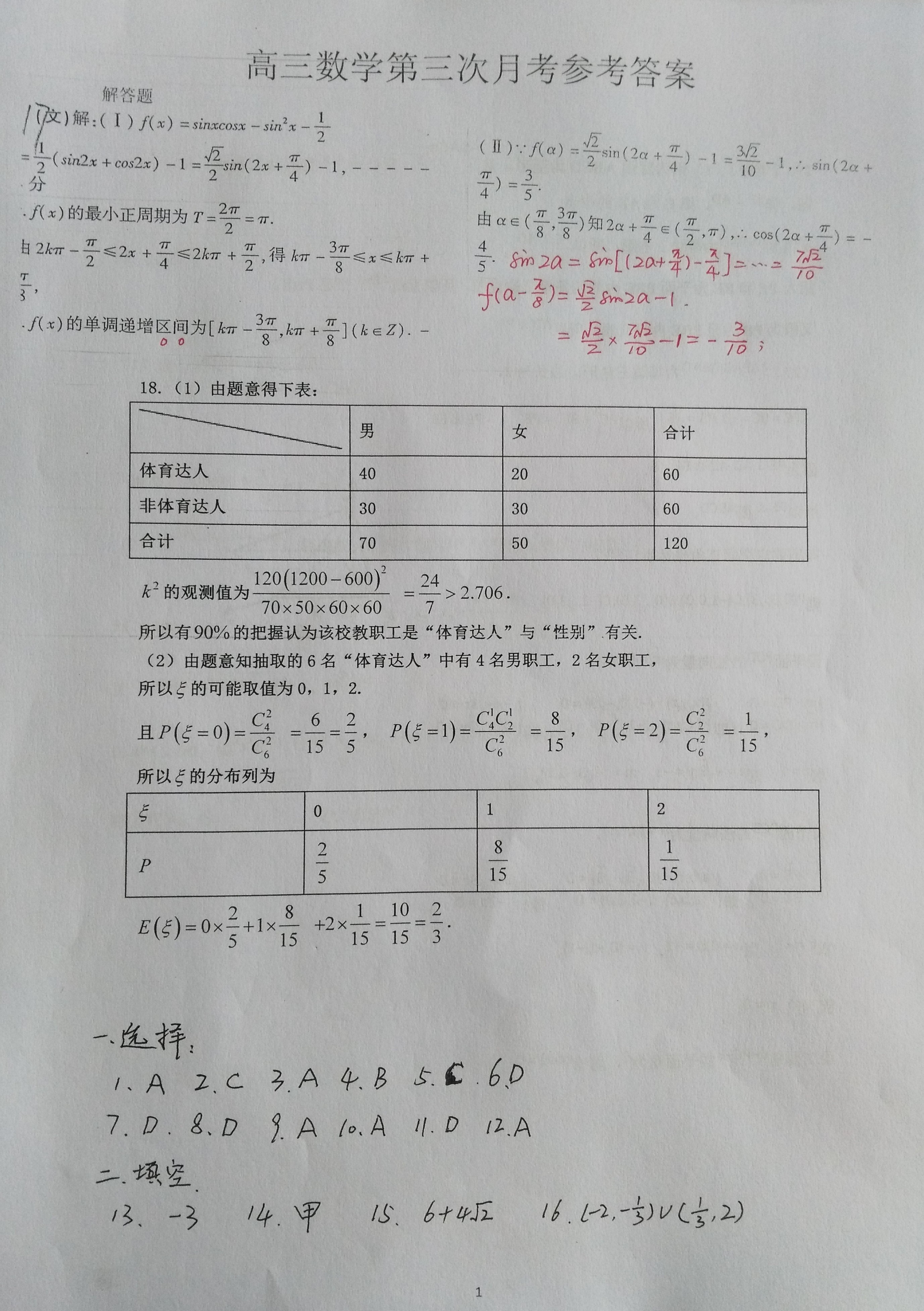




 2019届[月考01-03]高三理科数学试题参考答案
2019届[月考01-03]高三理科数学试题参考答案

 浙公网安备 33010602011771号
浙公网安备 33010602011771号