2018年全国卷Ⅲ卷文科数学解析
前言
从一个数学老师的角度来解析2018高考,结合学生的实际学情,给出学习建议。
选择题
解析1:图像法,先做出函数\(y=\ln x\)关于 \(y\) 轴对称的函数 \(y=\ln(-x)\) 的图像,再将其向右平移两个单位即可,得到\(y=ln[-(x-2)]=ln(2-x)\),故选 \(B\) .
解析2:待求解的函数图像上任取一点 \(P_0(x_0,y_0)\),则其关于直线 \(x=1\) 的对称点坐标为 \(P(2-x_0,y_0)\),则其必然满足 \(y=\ln x\),得到 \(y_0=ln(2-x_0)\),即 \(y=ln(2-x)\) ,故选 \(B\)。
解析3:由于点\((1,0)\)在给定函数图像上,也在对称轴上,则其必然也在所求函数图像上,代入验证,故选\(B\)。
【解析】 图像缺失,偶函数,\(f(0)=2\),\(f(1)=2\),故选D.
【整理理由】:用穿根法做函数\(y=f'(x)\)的图像,\(f'(x)=-4x^3+2x=-2x(2x^2-1)=-2x(\sqrt{2}x+1)(\sqrt{2}x+1)\)
先用手工做出函数\(y=x(\sqrt{2}x+1)(\sqrt{2}x+1)\)的图像,再做出函数\(y=-2x(\sqrt{2}x+1)(\sqrt{2}x+1)\)的图像,由此可以看出
函数\(f(x)\)在\((0,\cfrac{\sqrt{2}}{2})\)上单调递增,在\((\cfrac{\sqrt{2}}{2},+\infty)\)上单调递减。
填空题
【解析】:令函数\(g(x)=ln(\sqrt{x^2+1}-x)\) ,则\(g(x)+g(-x)=ln(\sqrt{x^2+1}-x)+ln(\sqrt{x^2+1}+x)=ln((\sqrt{x^2+1})^2-x^2)=ln1=0\),故函数\(g(x)\)为奇函数。
同理,\(f(x)+f(-x)=ln(\sqrt{x^2+1}-x)+1+ln(\sqrt{x^2+1}+x)+1=2\),即\(f(x)+f(-x)=2\),
\(f(a)+f(-a)=2\),\(f(a)=4\),得到\(f(-a)=-2\)。
【备注】:\(f(x)+f(-x)=2\),则函数\(f(x)\)关于点\((0,1)\)对称。
解答题
(1)求曲线\(y=f(x)\)在点\((0,-1)\)处的切线方程。
【解析】:\(f'(x)=\cfrac{(2ax+1)e^x-(ax^2+x-1)e^x}{(e^x)^2}=\cfrac{-ax^2+2ax-x+2}{e^x}\)
由\(f'(0)=2\),故由点斜式得到切线方程为\(y-(-1)=2(x-0)\),即\(2x-y-2=0\)。
(2)证明:当\(a\ge 1\)时,\(f(x)+e\ge 0\)。
证明【证明的难点是放缩】:
当\(a\ge 1\)时,\(f(x)+e\ge (x^2+x-1+e^{x+1})\cdot e^{-x}\),由于\(e^{-x}>0\)恒成立,故可以考虑甩掉她,
令\(g(x)=x^2+x-1+e^{x+1}\),则\(g'(x)=2x+1+e^{x+1}\),
【经验之谈:导数的解答题到此,我们可以这样寻找分界点,当题目中含有\(e^x\)时,可以考虑用\(x=0\)来尝试分界点,由于\(e^0=1\);当题目中含有\(lnx\)时,可以考虑用\(x=1\)来尝试分界点,由于\(ln1=0\)】
我们很容易发现,\(x=-1\)是分界点,故可以这样写结果,
当\(x<-1\)时,\(g'(x)<0\),\(g(x)\)单调递减,当\(x>-1\)时,\(g'(x)>0\),\(g(x)\)单调递增,
故\(g(x)_{min}=g(-1)=0\),故有\(g(x)\ge g(-1)=0\)
则\(g(x)\cdot e^{-x}\ge g(-1)\cdot e^{-x}=0\),即\(f(x)+e\ge 0\)。
【解后反思】注意不等式放缩。此题的解法同于2018高考一卷文科第21题(2)的解答思路。
(1)求\(\alpha\)的取值范围;
分析:先设出直线带斜率\(k\)的方程,再联立圆方程组成方程组,由于线与圆相交于两个点,则\(\Delta>0\) 或者圆心到直线的距离\(d < r=1\),都可以求解。不过在设直线方程时需要分类讨论;
【解析】当\(\alpha=\cfrac{\pi}{2}\)时,直线的斜率不存在,直线为\(x=0\)满足条件。
当\(\alpha=\cfrac{\pi}{2}\)时,设直线方程为\(y+\sqrt{2}=kx\),即直线为\(kx-y-\sqrt{2}=0\),\(\odot O\)的直角坐标方程为\(x^2+y^2=1\),故圆心到直线的距离\(d=\cfrac{|-\sqrt{2}|}{\sqrt{k^2+1}}<1\),
解得\(k^2>1\),即\(k>1\)或者\(k<-1\),借助\(y=tan\alpha(0\leq \alpha<\pi)\)的函数图像可知,
当\(k>1\)时,\(\cfrac{\pi}{4}<\alpha<\cfrac{\pi}{2}\),当\(k<-1\)时,\(\cfrac{\pi}{2}<\alpha<\cfrac{3\pi}{4}\),
综上所述,\(\alpha\)的取值范围为\((\cfrac{\pi}{4},\cfrac{3\pi}{4})\);
(2)求\(AB\)中点\(P\)的轨迹的参数方程。
分析:看到题目中的\(AB\)中点\(P\)时,你应该想到直线的参数方程中的一个常识:
设点\(A,B\)对应的参数分别为\(t_A,t_B\),线段\(AB\)的中点\(P\)对应的参数为\(t_P\),则有\(\cfrac{t_A+t_B}{2}=t_P\)
【解析】由题目设直线\(l\)的参数方程为\(\left\{\begin{array}{l}{x=t\cdot cos\alpha}\\{y=-\sqrt{2}+t\cdot sin\alpha}\end{array}\right.(t为参数,\cfrac{\pi}{4}<\alpha<\cfrac{3\pi}{4})\),
设\(A、B、P\)对应的参数分别为\(t_A、t_B、t_P\),则有\(t_P=\cfrac{t_A+t_B}{2}\),
将直线\(l\)的参数方程,代入圆\(O\)的直角坐标方程,整理得到\(t^2-2\sqrt{2}sin\alpha+1=0\),
则由韦达定理有\(t_A+t_B=2\sqrt{2}sin\alpha\),由中点坐标公式得到\(t_P=\sqrt{2}sin\alpha\),
又由于点\(P\)在直线\(l\)上,故满足直线的参数方程\(\left\{\begin{array}{l}{x=t_P\cdot cos\alpha}\\{y=-\sqrt{2}+t_P\cdot sin\alpha}\end{array}\right.\),
代入得到点\(P\)的轨迹的参数方程是\(\left\{\begin{array}{l}{x=\cfrac{\sqrt{2}}{2} sin2\alpha}\\{y=-\cfrac{\sqrt{2}}{2}-\cfrac{\sqrt{2}}{2} cos2\alpha}\end{array}\right.(\alpha为参数,\cfrac{\pi}{4}<\alpha<\cfrac{3\pi}{4})\),
【解后反思】1、注意设直线方程时的分类讨论。2、注意直线参数方程中的中点坐标公式\(\cfrac{t_A+t_B}{2}=t_P\)。
解析图片版

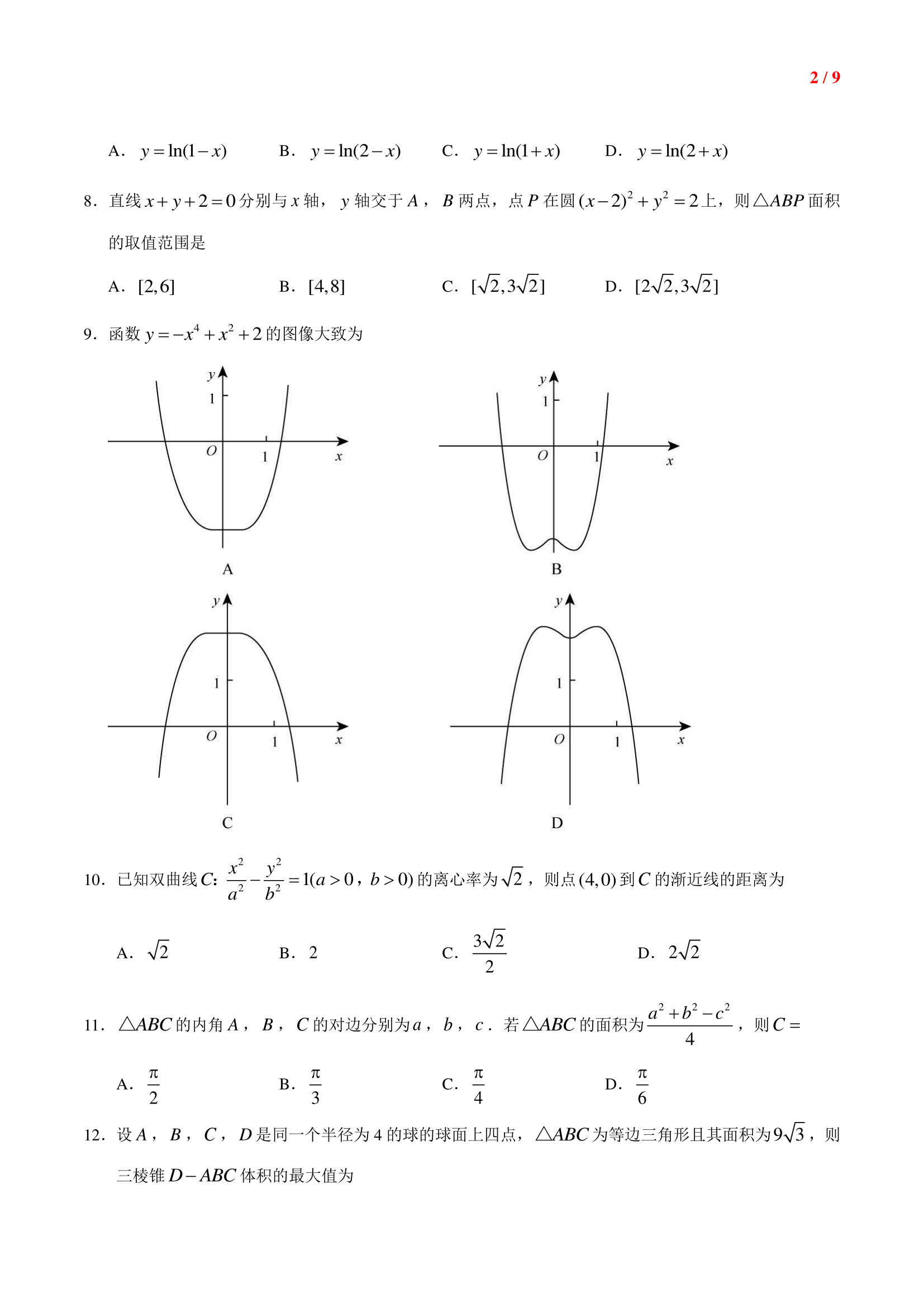


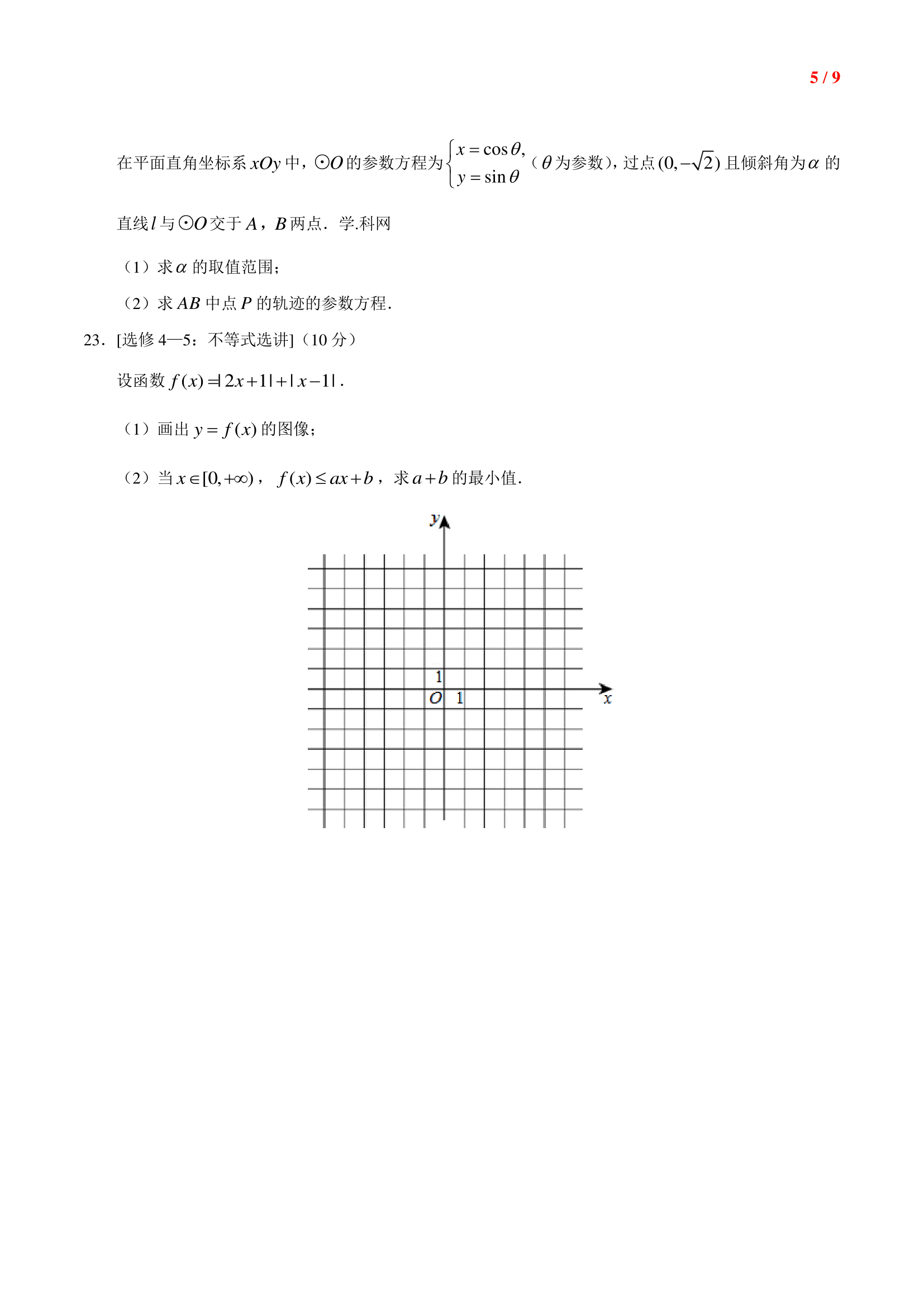






 浙公网安备 33010602011771号
浙公网安备 33010602011771号