借助比例因子简化运算

前言

涉及到比例的相关运算，如果能引入比例因子，可能会使得计算变得很简单，主要原因是整式的运算相比分式的运算要简单且不容易出错。尤其是涉及到连比的形式，更是如此。

相关素材

• 常用的勾股数：\(3n，4n，5n(n\in N^*)\)；\(5，12，13\)；\(7，24，25\)；\(8，15，17\)；\(9，40，41\)；
• 连比形式或比例形式，可以引入非零比例因子简化运算，这样的运算可能在解三角形中，圆锥曲线的运算，等比数列的相关运算中。^[1]

典例剖析

【2021届高三文数三轮模拟题】已知 \(S_n\)，\(T_n\) 分别为等差数列 \(\{a_n\}\) 和 \(\{b_n\}\) 的前 \(n\) 项和，若 \(\cfrac{S_n}{T_n}=\cfrac{2n+1}{3n+2}\)，则 \(\cfrac{a_5}{b_3}\)=___________.

解析： 由于等差数列的前 \(n\) 项和公式为 \(S_n=An^2+Bn=An(n+\cfrac{B}{A})\)，又由于 \(\cfrac{S_n}{T_n}=\cfrac{2n+1}{3n+2}\)，

[备注：说明 \(S_n\) 和 \(T_n\) 约去了相同的公因式，应该是关于 \(n\) 的一次式，不妨设为\(kn\)]

故可以设 \(S_n=kn(2n+1)\)，\(T_n=kn(3n+2)\)，

则 \(\cfrac{a_5}{b_3}=\cfrac{S_5-S_4}{T_3-T_2}=\cfrac{55k-36k}{33k-16k}=\cfrac{19k}{17k}=\cfrac{19}{17}\).

已知\(\theta\)为第三象限的角，且\(tan\theta=2\)，求\(sin\theta\)和\(cos\theta\)。

【法1】：常规方法，方程组法，由已知条件可得到，\(\left\{\begin{array}{l}{\cfrac{sin\theta}{cos\theta}=2}\\{sin^2\theta+cos^2\theta=1}\end{array}\right.\)，

解得\(\left\{\begin{array}{l}{sin\theta=-\cfrac{2\sqrt{5}}{5}}\\{cos\theta=-\cfrac{\sqrt{5}}{5}}\end{array}\right.\)，或\(\left\{\begin{array}{l}{sin\theta=\cfrac{2\sqrt{5}}{5}}\\{cos\theta=\cfrac{\sqrt{5}}{5}}\end{array}\right.(舍去)\)，

故有\(sin\theta=-\cfrac{2\sqrt{5}}{5}\)；\(cos\theta=-\cfrac{\sqrt{5}}{5}\)；

【法2】：三角函数定义法，简单方法。由于\(tan\theta=2\)，则角\(\theta\)的终边在射线\(y=2x\{x<0\}\)上，

故在射线\(y=2x\{x<0\}\)上取点\((-1，-2)\)，则由三角函数的定义可知，\(x=-1\)，\(y=-2\)，\(r=\sqrt{5}\)，

则\(sin\theta=\cfrac{y}{r}=\cfrac{-2}{\sqrt{5}}=-\cfrac{2\sqrt{5}}{5}\)；\(cos\theta=\cfrac{x}{r}=\cfrac{-1}{\sqrt{5}}=-\cfrac{\sqrt{5}}{5}\)；

【法3】：引入比例因子法，由\(tan\theta=\cfrac{sin\theta}{cos\theta}=2\)，\(\theta\)为第三象限的角，

可设\(sin\theta=2k\)，\(cos\theta=k(k<0)\)，

由于\(sin^2\theta+cos^2\theta=1\)，即\(5k^2=1\)，解得\(k=-\cfrac{\sqrt{5}}{5}\)，

故有\(sin\theta=-\cfrac{2\sqrt{5}}{5}\)；\(cos\theta=-\cfrac{\sqrt{5}}{5}\)；

【2017全国卷1理科第11题】已知 \(x、y、z\) 都是正数，且 \(2^x=3^y=5^z\)，则 【\(\qquad\)】

$A.2x<3y<5z$ $B.5z<2x<3y$ $C.3y<5z<2x$ $D.3y<2x<5z$

分析：由题目可知， \(x、y、z\) 都是正数，令\(2^x=3^y=5^z=k\)，则 \(k=2^x>2^0=1\)，\(\lg k>0\) .

则\(x=log_2k=\cfrac{lgk}{lg2}\)，\(y=log_3k=\cfrac{lgk}{lg3}\)，\(z=log_5k=\cfrac{lgk}{lg5}\)，

故\(2x=\cfrac{2lgk}{lg2}=\cfrac{lgk}{\cfrac{1}{2}lg2}=\cfrac{lgk}{lg\sqrt{2}}\)，\(3y=\cfrac{3lgk}{lg3}=\cfrac{lgk}{\cfrac{1}{3}lg3}=\cfrac{lgk}{lg\sqrt[3]{3}}\)，

\(5z=\cfrac{5lgk}{lg5}=\cfrac{lgk}{\cfrac{1}{5}lg5}=\cfrac{lgk}{lg\sqrt[5]{5}}\)，接下来，下面的解法都用到上述的结果：

法1：(单调性法)转化为只需要比较\(\sqrt[2]{2}\)，\(\sqrt[3]{3}\)，\(\sqrt[5]{5}\)三者的大小即可。

先比较\(\sqrt[2]{2}\)，\(\sqrt[3]{3}\)，给两个式子同时6次方，

得到\((\sqrt[2]{2})^6=2^3=8\)，\((\sqrt[3]{3})^6=3^2=9\)，

故\(\sqrt[2]{2}<\sqrt[3]{3}\)，则\(\cfrac{lgk}{lg\sqrt[2]{2}}>\cfrac{lgk}{lg\sqrt[3]{3}}\)，

即得到\(2x>3y\)

再比较\(\sqrt[2]{2}\)，\(\sqrt[5]{5}\)，给两个式子同时10次方，

得到\((\sqrt[2]{2})^{10}=2^5=32\)，\((\sqrt[5]{5})^{10}=5^2=25\)，

故\(\sqrt[2]{2}>\sqrt[5]{5}\)，则\(\cfrac{lgk}{lg\sqrt[2]{2}}<\cfrac{lgk}{lg\sqrt[3]{3}}\)，

即得到\(5z>2x\)，综上得到\(3y<2x<5z\)，故选 \(D\) .

法2：(作差法)，令\(2^x=3^y=5^z=k\)，则 \(k=2^x>2^0=1\)，则 \(\lg k>0\)；

\(2x-3y=\cfrac{2\lg k}{lg2}-\cfrac{3\lg k}{lg3}=\cfrac{\lg k(2lg3-3lg3)}{lg2lg3}=\cfrac{\lg k(lg9-lg8)}{lg2lg3}>0\)，故\(2x>3y\);

\(2x-5z=\cfrac{2\lg k}{lg2}-\cfrac{5\lg k}{lg5}=\cfrac{\lg k(2lg5-5lg2)}{lg2lg5}=\cfrac{\lg k(lg25-lg32)}{lg2lg5}<0\)，故\(2x<5z\);

综上有\(3y<2x<5z\)，故选 \(D\) .

法3：(作商法)

\(\cfrac{2x}{3y}=\cfrac{2}{3}\cdot \cfrac{lg3}{lg2}=\cfrac{lg9}{lg8}=log_89>1\)，故\(2x>3y\)；

\(\cfrac{5z}{2x}=\cfrac{5}{2}\cdot \cfrac{lg2}{lg5}=\cfrac{lg2^5}{lg5^2}=log_{25}32>1\)，

故\(5z>2x\)；故 \(3y<2x<5z\)，故选 \(D\) .

已知\(a，b>0\)，且满足\(2+log_2a=3+log_3b=log_6(a+b)\)，求\(\cfrac{1}{a}+\cfrac{1}{b}\)的值；

分析：引入正数因子\(k\)，

令\(2+log_2a=3+log_3b=log_6(a+b)=k(k>0)\)，

则由\(2+log_2a=log_2(4a)=k\)，

得到\(4a=2^k\)，即\(a=\cfrac{2^k}{2^2}=2^{k-2}\)；

由\(3+log_3b=log_3(27b)=k\)，

得到\(27b=3^k\)，即\(b=\cfrac{3^k}{3^3}=3^{k-3}\)；

由\(log_6(a+b)=k\)，

得到\(a+b=6^k\)；

则\(\cfrac{1}{a}+\cfrac{1}{b}=\cfrac{a+b}{ab}=\cfrac{6^k}{2^{k-2}\cdot 3^{k-3}}=\cfrac{2^k\cdot 3^k}{2^k\cdot 2^{-2}\cdot 3^k\cdot 3^{-3}}\)

\(=\cfrac{1}{2^{-2}\cdot 3^{-3}}=2^2\cdot 3^3=108\)

已知\(2^x=3^y\)，求\(\cfrac{x}{y}\)的值。

分析：令\(2^x=3^y=k\)，则\(x=log_2k=\cfrac{1}{log_k2}\)，\(y=log_3k=\cfrac{1}{log_k3}\)，

故\(\cfrac{x}{y}=\cfrac{\frac{1}{log_k2}}{\frac{1}{log_k3}}=\cfrac{log_k3}{log_k2}=log_23=\cfrac{lg3}{lg2}\)。

【2019届高三理科数学三轮模拟试题】已知平面向量\(\vec{a}\)、\(\vec{b}\)满足\((\vec{a}-2\vec{b})\perp (3\vec{a}+\vec{b})\)，且\(|\vec{a}|=\cfrac{1}{2}|\vec{b}|\)，则向量\(\vec{a}\)与\(\vec{b}\)的夹角的正弦值为【】

$A.\cfrac{1}{2}$ $B.-\cfrac{1}{2}$ $C.\cfrac{\sqrt{3}}{2}$ $D.-\cfrac{\sqrt{3}}{2}$

分析：由题可知，\((\vec{a}-2\vec{b})\cdot (3\vec{a}+\vec{b})=0\)，化简得到，\(3\vec{a}^2-5\vec{a}\cdot \vec{b}-2\vec{b}^2=0\)①，

由\(|\vec{a}|=\cfrac{1}{2}|\vec{b}|\)，可设\(|\vec{a}|=t(t>0)\)，则\(|\vec{b}|=2t\)，代入①式，

得到\(-10t^2cos\theta+5t^2=0\)，得到\(cos\theta=\cfrac{1}{2}\)，则\(sin\theta=\cfrac{\sqrt{3}}{2}\)，故选\(C\).

【2019届高三理科数学三轮模拟训练题】公元前6世纪，黄金分割被毕达哥拉斯学派发现，公元前4世纪，古希腊数学家欧多克索斯第一个系统研究了这一问题，并建立起比例理论。欧几里得在《几何原本》中论及正五边形有关黄金分割的定理：正五边形\(ABCDE\)中，\(AD\)，\(BE\)交于点\(H\)，则\(H\)为\(AD\)的黄金分割点，即\(\frac{AH}{HD}=\frac{\sqrt{5}-1}{2}\)，现从如图所示的正五边形中任取一点，则该点恰好取自阴影部分的概率是【】

$A.\cfrac{2}{5}$ $B.\cfrac{\sqrt{5}}{5}$ $C.\cfrac{4}{7}$ $D.\cfrac{2+\sqrt{5}}{7}$

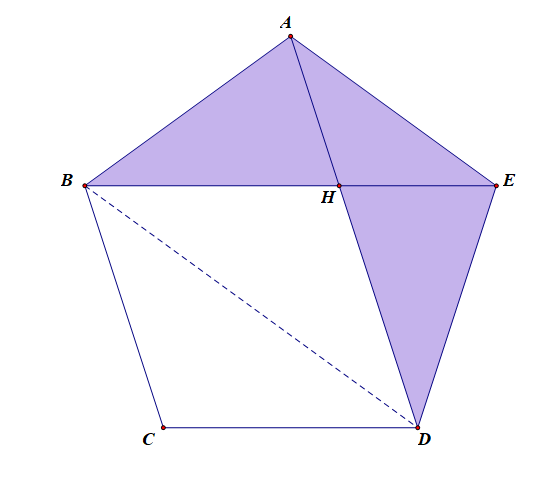
法1分析：由\(\frac{AH}{HD}=\frac{\sqrt{5}-1}{2}\)，借助比例因子，则可设\(S_{\triangle AEH}=(\sqrt{5}-1)k(k>0)\)，\(S_{\triangle DEH}=2k\)，

且有\(S_{\triangle AHB}=S_{\triangle DHE}\)，又由于正五边形的对称性可知，\(S_{\triangle ABE}=S_{\triangle BCD}\)，\(S_{\triangle BCD}=S_{\triangle BDH}\)，

则\(S_{\triangle ABE}=(\sqrt{5}-1)k+2k=(\sqrt{5}+1)k\)，则\(S_{阴影}=2k+2k+(\sqrt{5}-1)k=(3+\sqrt{5})k\)，\(S_{正}=2k+3\cdot (\sqrt{5}+1)k=(5+3\sqrt{5})k\)，

故所求概率为\(P=\cfrac{S_{阴影}}{S_{正}}=\cfrac{(3+\sqrt{5})k}{(5+3\sqrt{5})k}=\cfrac{\sqrt{5}}{5}\)。

在\(\triangle ABC\)中，已知\(\cfrac{a}{cosA}=\cfrac{b}{cosB}=\cfrac{c}{cosC}\)，求三角形的三个角的大小。

分析：令\(\cfrac{a}{cosA}=\cfrac{b}{cosB}=\cfrac{c}{cosC}=k\)，

则有\(cosA=\cfrac{a}{k}\)，\(cosB=\cfrac{b}{k}\)，\(cosC=\cfrac{c}{k}\)，

再结合\(sinA=\cfrac{a}{2R}\)，\(sinB=\cfrac{b}{2R}\)，\(sinC=\cfrac{c}{2R}\)，

故有\(tanA=tanB=tanC=\cfrac{k}{2R}\)，故\(A=B=C=\cfrac{\pi}{3}\)。

设等比数列\(\{a_n\}\)的前\(n\)项的和为\(S_n\)，若\(\cfrac{S_6}{S_3}=\cfrac{1}{2}\)，则\(\cfrac{S_9}{S_6}\)=？

分析：引入比例因子，设\(\cfrac{S_6}{S_3}=\cfrac{1}{2}=\cfrac{k}{2k}(k\neq 0)\)，则\(S_6=k\)，\(S_3=2k\)，

\(S_6-S_3=-k\)，由\(S_3，S_6-S_3，S_9-S_6\)成等比数列，可知\(S_9-S_6=\cfrac{k}{2}\)

则\(S_9=\cfrac{3k}{2}\)，故\(\cfrac{S_9}{S_6}=\cfrac{\cfrac{3k}{2}}{2k}=\cfrac{3}{4}\)。

设等比数列\(\{a_n\}\)的前\(n\)项的和为\(S_n\)，若\(\cfrac{S_6}{S_3}=\cfrac{1}{2}\)，则\(\cfrac{S_9}{S_6}\)=？

分析：引入比例因子，设\(\cfrac{S_6}{S_3}=\cfrac{1}{2}=\cfrac{k}{2k}(k\neq 0)\)，则\(S_6=k\)，\(S_3=2k\)，

\(S_6-S_3=-k\)，由\(S_3，S_6-S_3，S_9-S_6\)成等比数列，可知\(S_9-S_6=\cfrac{k}{2}\)

则\(S_9=\cfrac{3k}{2}\)，故\(\cfrac{S_9}{S_6}=\cfrac{\cfrac{3k}{2}}{2k}=\cfrac{3}{4}\)。

已知双曲线\(C\)的离心率为\(\cfrac{5}{2}\)，左、右焦点为\(F_1\)，\(F_2\)，点\(A\)在\(C\)上，若\(|F_1A|=2|F_2A|\)，则\(cos\angle AF_2F_1\)=_______.

分析：由\(e=\cfrac{c}{a}=\cfrac{5}{2}\)，令\(c=5k(k>0)\)，则\(a=2k\)，\(b=\sqrt{21}k\)，

不妨令双曲线的焦点在\(x\)轴，点\(A\)在其右支上，则由双曲线的定义可知，

\(|F_1A|-|F_2A|=2a=4k\)，又\(|F_1A|=2|F_2A|\)，

则\(|F_2A|=4k\)，\(|F_1A|=8k\)，又\(|F_1F_2|=10k\)，

利用余弦定理可知\(cos\angle AF_2F_1=\cdots=\cfrac{13}{20}\)；

【2020 \(\cdot\) 江州质检】【启迪思维题目】正数\(a\)， \(b\)， \(c\) 满足 \(3^{a}=4^{b}=6^{c}\)， 则下列关系正确的是【\(\quad\)】

$A.\cfrac{1}{c}=\cfrac{1}{a}+\cfrac{1}{b}$ $B.\cfrac{2}{c}=\cfrac{2}{a}+\cfrac{1}{b}$ $C.\cfrac{1}{c}=\cfrac{2}{a}+\cfrac{2}{b}$ $D.\cfrac{2}{c}=\cfrac{1}{a}+\cfrac{2}{b}$

解析： 因为 \(a\)， \(b\)， \(c\) 均为正数, 设 \(3^{a}=4^{b}=6^{c}=k\)，则 \(k>0\)，到此，实现了变量集中；

所以 \(a=\log_{3}k\)， \(b=\log_{4}k\)， \(c=\log_{6}k\)，

则 \(\cfrac{1}{a}=\cfrac{\lg3}{\lg k}\)， \(\cfrac{1}{b}=\cfrac{\lg4}{\lg k}\)， \(\cfrac{1}{c}=\cfrac{\lg6}{\lg k}\)，

由于 \(\cfrac{2}{c}\)\(=\)\(\cfrac{2\lg 6}{\lg k}\)\(=\)\(\cfrac{2\lg3}{\lg k}\)\(+\)\(\cfrac{\lg 4}{\lg k}\)\(=\)\(\cfrac{2}{a}\)\(+\)\(\cfrac{1}{b}\)，故选 \(B\) .

【2020 \(\cdot\) 江州质检】【启迪思维题目】设 \(x\)， \(y\)， \(z\) 均大于 \(1\)， 且 \(\log_{\sqrt{2}}\cfrac{1}{x}=\log _{\sqrt{3}}\cfrac{1}{y}=\log_{\sqrt{6}}\cfrac{1}{z}\)， 令\(a=x^{\frac{1}{2}}\)， \(b=y^{\frac{1}{3}}\)，\(c=z^{\frac{1}{6}}\)， 则 \(a\)， \(b\)， \(c\) 的大小关系是 【\(\quad\)】

$A.a > b > c$ $B.b > c >a$ $C.c > a >b$ $D.b > a >c$

解析 ： 由于\(\log_{\sqrt{2}}\cfrac{1}{x}=\log _{\sqrt{3}}\cfrac{1}{y}=\log_{\sqrt{6}}\cfrac{1}{z}\)， 化简： \(\log_{\sqrt{2}}\cfrac{1}{x}=-\log_{\sqrt{2}}x\)，

故 \(\log _{\sqrt{2}} x=\log _{\sqrt{3}} y=\log _{\sqrt{6}} z\)，

令 \(\log _{\sqrt{2}} x=\log _{\sqrt{3}} y=\log _{\sqrt{6}} z=k\)，

由于 \(x\)， \(y\)， \(z\) 均大于 \(1\)， 所以 \(k>0\)，

所以有 \(x=2^{\frac{k}{2}}\)， \(y=3^{\frac{k}{2}}\)， \(z=6^{\frac{k}{2}}\)，到此，实现了变量集中；

所以 \(a=x^{\frac{1}{2}}=2^{\frac{k}{4}}\)， \(b=y^{\frac{1}{3}}=3^{\frac{k}{6}}\)， \(c=z^{\frac{1}{6}}=6^{\frac{k}{12}}\)，

可得\(a\)， \(b\)， \(c\) 均大于 \(1\)，

所以 \(a^{12}=8^{k}\)， \(b^{12}=9^{k}\)， \(c^{12}=6^{k}\)，

即 \(9^{k}>8^{k}>6^{k}\)，即\(b^{12}>a^{12}>c^{12}\)，

所以 \(b>a>c\)， 故选 \(D\) .

【2021届高三文数三轮模拟题】《数书九章》三斜求积术“以小斜幂，并大斜幂减中斜幂，余半之，自乘于上；以小斜幂乘大斜幂减上，余四约之，为实；一为从隅，开平方得积” . 中国古代数学家秦九韶把三角形的三条边分别称为小斜、中斜和大斜. “术”即方法，以 \(S\)， \(a\)， \(b\)， \(c\) 分别表示三角形面积、大斜、中斜、小斜，所以 \(S=\sqrt{\cfrac{1}{4}[a^{2}\times b^{2}-(\cfrac{a^{2}+b^{2}-c^{2}}{2})^{2}]}\) . 已知 \(\triangle ABC\) 的三边长分别为 \(a\)， \(b\)， \(c\) ，对应的高分别为 \(h_{a}\)， \(h_{b}\)， \(h_{c}\)， 若 \(h_{a}\) \(:\) \(h_{b}\) \(:\) \(h_{c}\)=\(3\) \(:\) \(4\) \(:\) \(6\)， \(a=4\) ， 则 \(\triangle ABC\) 的面积为【\(\quad\)】

$A.\cfrac{9}{16}$ $B.\cfrac{3}{4}$ $C.\cfrac{135}{16}$ $D.\cfrac{3\sqrt{15}}{4}$

分析：由于 \(h_{a}\) \(:\) \(h_{b}\) \(:\) \(h_{c}\)=\(3\) \(:\) \(4\) \(:\) \(6\)，

则 \(h_a=3k\) ， \(h_b=4k\) ， \(h_c=6k\) ，\(k>0\)，

由于\(S=\cfrac{1}{2}a\cdot h_a=\cfrac{1}{2}b\cdot h_b=\cfrac{1}{2}c\cdot h_c\)

则 \(a:b:c=\cfrac{2S}{h_a}:\cfrac{2S}{h_b}:\cfrac{2S}{h_c}\) [给每一项都除以 \(2S\) ]

\(=\cfrac{1}{h_a}:\cfrac{1}{h_b}:\cfrac{1}{h_c}\)

\(=\cfrac{1}{3k}:\cfrac{1}{4k}:\cfrac{1}{6k}\) [给每一项都乘以 \(k\)，再同乘以 \(12\) ]

\(=4:3:2\)， 即 \(a:b:c=4:3:2\)，

又由于 \(a=4\)，故 \(b=3\)，\(c=2\)，将其代入\(S=\sqrt{\cfrac{1}{4}[a^{2}\times b^{2}-(\cfrac{a^{2}+b^{2}-c^{2}}{2})^{2}]}\)，

计算得到，\(S=\sqrt{\cfrac{1}{4}[4^{2}\times 3^{2}-(\cfrac{4^{2}+3^{2}-2^{2}}{2})^{2}]}=\cfrac{3\sqrt{15}}{4}\)，故选 \(D\).

【2021届高三文数三轮模拟题】已知 \(S_n\)，\(T_n\) 分别为等差数列 \(\{a_n\}\) 和 \(\{b_n\}\) 的前 \(n\) 项和，若 \(\cfrac{S_n}{T_n}=\cfrac{2n+1}{3n+2}\)，则 \(\cfrac{a_5}{b_3}\)=___________.

解析： 由于等差数列的前 \(n\) 项和公式为 \(S_n=An^2+Bn=An(n+\cfrac{B}{A})\)，又由于 \(\cfrac{S_n}{T_n}=\cfrac{2n+1}{3n+2}\)，

[备注：说明 \(S_n\) 和 \(T_n\) 约去了相同的公因式，应该是关于 \(n\) 的一次式，不妨设为\(kn\)]

故可以设 \(S_n=kn(2n+1)\)，\(T_n=kn(3n+2)\)，

则 \(\cfrac{a_5}{b_3}=\cfrac{S_5-S_4}{T_3-T_2}=\cfrac{55k-36k}{33k-16k}=\cfrac{19k}{17k}=\cfrac{19}{17}\).

对应练习

【2022届高三数学三轮模拟冲刺试题】设 \(a\)、\(b\)、\(c\) 都是正数，且 \((\cfrac{1}{4})^a=(\cfrac{1}{6})^b=(\cfrac{1}{9})^c\)，那么 【\(\qquad\)】

$A.\cfrac{1}{a}+\cfrac{1}{b}=\cfrac{1}{c}$ $B.\cfrac{1}{b}+\cfrac{1}{c}=\cfrac{1}{a}$ $C.\cfrac{1}{a}+\cfrac{1}{b}=\cfrac{2}{c}$ $D.\cfrac{1}{a}+\cfrac{1}{c}=\cfrac{2}{b}$

提示： 由于 \(\cfrac{1}{4^a}=\cfrac{1}{6^b}=\cfrac{1}{9^c}\)，故可以设 \(4^a=6^b=9^c=M\)，其余运算略，选 \(D\) .

---

1. 如三角形的三边之比为\(a\) ：\(b\) ：\(c\)=\(2\) ：\(3\) ：\(4\)，则可以设\(a=2k\)，\(b=3k\)，\(c=4k(k>0)\)；如果求最大(小)角的余弦值，就可以直接代入余弦定理计算，同时\(a\)，\(b\)，\(c\)都是\(k\)的一元函数了。
   同样的思路也可以用到圆锥曲线中，比如已知离心率\(e=\cfrac{c}{a}=\sqrt{3}\)，则可知\(c=\sqrt{3}t，a=t(t>0)\) ，则有\(b=\sqrt{2}t\)； ↩︎