2018宝鸡市高三数学第一次质量检测

题目解析

【2018宝鸡市高三数学第一次质量检测第9题】若\(sin(\alpha-\cfrac{\pi}{4})=-cos2\alpha\)，则\(sin2\alpha\)的值为【】

$A.\cfrac{1}{2}$ $B.-\cfrac{1}{2}$ $C.\cfrac{3}{4}$ $D.-\cfrac{3}{4}$

分析：本题目属于三角函数求值中的给值求值，观察所给三角函数式，由于左右两边的角不一样，所以想到将角统一，

同时想到\(sin(\alpha-\cfrac{\pi}{4})=\cfrac{\sqrt{2}}{2}(sin\alpha-cos\alpha)\)，故化角时采用\(cos^2\alpha-sin^2\alpha\)的形式。

原式变形为\(\cfrac{\sqrt{2}}{2}(sin\alpha-cos\alpha)=-(cos^2\alpha-sin^2\alpha)=(sin\alpha-cos\alpha)(sin\alpha+cos\alpha)\)

则有\(sin\alpha+cos\alpha=\cfrac{\sqrt{2}}{2}\)，两边平方得到\(1+2sin\alpha\cdot cos\alpha=\cfrac{1}{2}\)

则有\(2sin\alpha\cdot cos\alpha=sin2\alpha=-\cfrac{1}{2}\)，故选\(B\).

【2018宝鸡市高三数学第一次质量检测第10题】某医务人员说：“包括我在内，我们社区诊所医生和护士共有17名。无论是否把我算在内，下面说法都是对的。在这些医务人员中：医生不少于护士；女护士多于男医生；男医生比女医生多；至少有两名男护士。”请你推断说话人的性别与职业是【】

$A.\textbf{男医生}$ $B.\textbf{男护士}$ $C.\textbf{女医生}$ $D.\textbf{女护士}$

分析：设男医生为\(a\)个，女医生为\(b\)个，女护士为\(c\)个，男护士为\(d\)个，则由题目可知

\(\begin{cases}&a+b+c+d=17\\&a+b\ge c+d\\&c>a\\&a>b\\&d\ge 2\end{cases}\)，由于\(b-d\ge c-a>0\)，故\(b>d\)，

故得到\(c>a>b>d\ge 2\)。

当\(d=2\)时，我们可以依次给其他三个变量赋值，比如\(c(5)>a(4)>b(3)>d(2)\)，此时不满足和为17；

再换一组比如\(c(8)>a(4)>b(3)>d(2)\)，又不满足\(a+b\ge c+d\)，

这样一路测试下来，只有\(c(6)>a(5)>b(4)>d(2)\)是满足所有条件的，而且此时只有\(b-1=3\)，

还满足刚才的式子，说明那个人只能是女医生；

当\(d>2\)，比如\(d=3\)时，仿上赋值\(c(6)>a(5)>b(4)>d(3)\)，或者其他的赋值方式，都是不符合题意的，

综上所述，那个人只能是女医生；故选C.

反思总结 ：这样的题目我们往往不知道从何入手，但是当我们把题目转化为不等式组这个数学模型时，我们就有了切入点了。

【2018宝鸡市高三数学第一次质量检测第12题】在平面直角坐标系中的\(A、B\)两点满足：①点\(A、B\)都在函数\(f(x)\)上；②点\(A、B\)关于原点对称，则称点\((A，B)\)是函数\(f(x)\)的一个“姊妹点对”。点\((A，B)\)和点\((B，A)\)可以看作同一个“姊妹点对”，已知函数\(f(x)=\begin{cases}x^2+2x，&x<0\\\cfrac{2}{e^x}，&x\ge 0\end{cases}\)，则函数\(f(x)\)的“姊妹点对”有【】

$A.0$ $B.1$ $C.2$ $D.3$

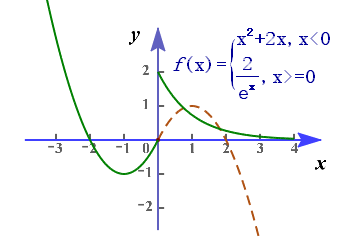
分析：当我们做出函数的整体图像后，应该想到新定义就是问我们：分段函数的一段上有几个点和分段函数另一段上的点是关于原点对称的。本题目考查思维之处在于，你能否想到将一个分段函数的两段图像上的点关于原点的对称问题，转化为其一段图像如\(y=\cfrac{2}{e^x}(x>0)\)和另一段图像\(y=x^2+2x(x\leq 0)\)关于原点对称的图像\(y=-x^2+2x(x>0)\)的交点个数问题。另一个考查之处就是手工作图像的能力。
做出适合题意的图像，由图像可知“姊妹点对”有2个，故选C。

【2018宝鸡市高三数学第一次质量检测第17题】已知数列\(\{a_n\}\)的前\(n\)项和为\(S_n\)，首项为\(a_1\)，且\(\cfrac{1}{2}\)，\(a_n\)，\(S_n\)构成等差数列，

(1). 求数列\(\{a_n\}\)的通项公式\(a_n\)；

分析：由题目\(\cfrac{1}{2}\)，\(a_n\)，\(S_n\)构成等差数列可知，\(2a_n=\cfrac{1}{2}+S_n\)，

即当\(n\ge 1\)时，\(S_n=2a_n-\cfrac{1}{2}①\)，

当\(n\ge 2\)时，\(S_{n-1}=2a_{n-1}-\cfrac{1}{2}②\)，

①-②得到，当\(n\ge 2\)时，\(a_n=S_n-S_{n-1}=2a_n-2a_{n-1}\)，

即\(a_n=2a_{n-1}(n\ge 2)\)，

令\(2a_n=\cfrac{1}{2}+S_n\)中的\(n=1\)，得到\(a_1=\cfrac{1}{2}\)，

故数列\(\{a_n\}\)是首项为\(\cfrac{1}{2}\)，公比为\(2\)的等比数列，

则有\(a_n=\cfrac{1}{2}\cdot 2^{n-1}=2^{n-2}(n\in N^*)\)。

反思总结：

1、题目中的条件“\(\cfrac{1}{2}\)，\(a_n\)，\(S_n\)构成等差数列”变为“\(a_n\)是\(\cfrac{1}{2}\)和\(S_n\)等差中项”，题目的求解过程和结果还是一样的。

2、本题目属于由\(a_n\)和\(S_n\)的关系求\(a_n\)，要是看不懂，你可以先变形为\(S_n=2a_n-\cfrac{1}{2}=f(a_n)\)的形式，然后联想你的知识储备就能找到求解方法了。

3、注意对\(n=1\)的验证，尽管这一步很简单，但是占了整个解题的份额的一半。
4、见到\(a_n=2a_{n-1}\)，就想到\(\cfrac{a_n}{a_{n-1}}=2\)，这是不对的，因为你没有想到分母不等于0的情形，换句话说要写出分式形式，得验证分母\(a_{n-1}\neq 0\)，递推到最终，要验证\(a_1\neq 0\)

(2). 数列\(b_n\)满足\(b_n=(log_2\;a_{2n+1})\cdot (log_2\;a_{2n+3})\)，【文】试求\(\cfrac{1}{b_1}+\cfrac{1}{b_2}+\cfrac{1}{b_3}+\cdots+\cfrac{1}{b_n}\).

【文科】由(1)可知，\(a_n=2^{n-2}\)，则\(a_{2n+1}=2^{2n-1}\)，\(a_{2n+3}=2^{2n+1}\)，

则\(b_n=(log_2\;a_{2n+1})\cdot (log_2\;a_{2n+3})=(log_2\;2^{2n-1})\cdot (log_2\;2^{2n+1})=(2n-1)\cdot (2n+1)\)，

则\(\cfrac{1}{b_n}=\cfrac{1}{(2n-1)\cdot (2n+1)}=\cfrac{1}{2}(\cfrac{1}{2n-1}-\cfrac{1}{2n+1})\)，

则\(\cfrac{1}{b_1}+\cfrac{1}{b_2}+\cfrac{1}{b_3}+\cdots+\cfrac{1}{b_n}\)，

\(=\cfrac{1}{2}[(1-\cfrac{1}{3})+(\cfrac{1}{3}-\cfrac{1}{5})+\cdots+(\cfrac{1}{2n-1}-\cfrac{1}{2n+1})]\)

\(=\cfrac{1}{2}(1-\cfrac{1}{2n+1})=\cfrac{n}{2n+1}\)

【理】 数列\(b_n\)满足\(b_n=(log_2\;a_{2n+1})\cdot (log_2\;a_{2n+3})\)，证明\(\cfrac{1}{b_1}+\cfrac{1}{b_2}+\cfrac{1}{b_3}+\cdots+\cfrac{1}{b_n}<\cfrac{1}{2}\).

【理科】接上，\(=\cdots=\cfrac{1}{2}(1-\cfrac{1}{2n+1})=\cfrac{1}{2}-\cfrac{1}{2}\cdot \cfrac{1}{2n+1}<\cfrac{1}{2}\)。

反思总结：

1、求解\(b_n\)时，特别要注意对数的运算性质；

2、求解\(T_n\)时，往往需要从其通项公式\(\cfrac{1}{b_n}\)入手分析，有了这个通项公式的依托，其他项的值就是赋值计算了。

3、理科题目的证明涉及到了放缩法，用到的模型是\(\cfrac{1}{2}-\textbf{正数}<\cfrac{1}{2}\)；

【2018宝鸡市高三数学第一次质量检测第21题】已知函数\(f(x)=\cfrac{x}{lnx}+ax，x>1\)；(1).若函数\(f(x)\)在区间\((1，+\infty)\)上单调递减，求实数\(a\)的取值范围；
(1). 切入点：函数\(f(x)\)在某区间单调递减，则导函数\(f'(x)\leq 0\)在此区间恒成立(本来还需要验证\(a\)的取值不能使原函数成为常函数，此题中口算验证就可以)。

\(f'(x)=\cfrac{lnx-1}{ln^2x}+a\)，由题可知\(f'(x)=\cfrac{lnx-1}{ln^2x}+a\leq 0\)在区间\((1，+\infty)\)上恒成立，

分离参数得到，\(a\leq \cfrac{1-lnx}{ln^2x}=\cfrac{1}{ln^2x}-\cfrac{1}{lnx}\)，

令\(g(x)=\cfrac{1}{ln^2x}-\cfrac{1}{lnx}\)，此时只需要求出\(g(x)_{min}\)即可。

为了求得\(g(x)_{min}\)，我们可以考虑导数法，不过如果能注意到函数的结构特征，还可以有其他的选择。

思路1(二次函数法)：令\(lnx=t\)，则由于\(x>1\)，得到\(lnx=t>0\)，这样\(g(x)=\cfrac{1}{ln^2x}-\cfrac{1}{lnx}=(\cfrac{1}{t})^2-\cfrac{1}{t}=h(t)\)

\(h(t)=(\cfrac{1}{t}-\cfrac{1}{2})^2-\cfrac{1}{4}\)，

当\(\cfrac{1}{t}=\cfrac{1}{2}\)，即\(t=2=lnx\)，即\(x=e^2>1\)时，\(h(t)_{min}=g(x)_{min}=-\cfrac{1}{4}\)，

故实数\(a\)的取值范围为\(a\leq -\cfrac{1}{4}\)，即\(a\in(-\infty，-\cfrac{1}{4}]\)。

思路2(导数法)：令\(g(x)=\cfrac{1-lnx}{ln^2x}\)，则\(g'(x)=\cfrac{(1-lnx)'\cdot ln^2x-(1-lnx)\cdot 2lnx\cdot \cfrac{1}{x}}{(ln^2x)^2}\)

\(g'(x)=\cfrac{-\cfrac{1}{x}\cdot ln^2x-(1-lnx)\cdot \cfrac{2}{x}\cdot lnx}{ln^4x}=\cfrac{-\cfrac{1}{x}\cdot lnx-\cfrac{2}{x}+\cfrac{2}{x}\cdot lnx}{ln^3x}\)

\(g'(x)=\cfrac{\cfrac{1}{x}\cdot lnx-\cfrac{2}{x}}{ln^3x}=\cfrac{\cfrac{1}{x}(lnx-2)}{ln^3x}\)

由于\(x>1\)，故\(g'(x)\)的表达式中的因子\(\cfrac{1}{x}>0\)和分母\(ln^3x>0\)，故我们到时候解不等式，就可以只解\(lnx-2>0(lnx-2<0)\)，

当然如果我们能借助导函数的部分\(y=lnx-2\)的图像，就可以直接读出解集来，这也就是数形结合思想给我们的启示。

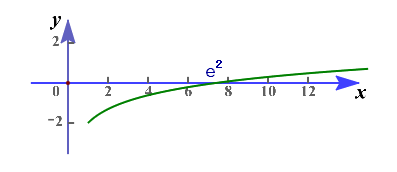
由图可知当\(x\in(1，e^2)\)时，\(lnx-2<0\)，即\(g'(x)<0\)；当\(x>e^2\)时，\(lnx-2>0\)，即\(g'(x)>0\)；

故\(g'(x)\)在\((1，e^2]\)上单调递减，在\([e^2，+\infty)\)上单调递增；

故\(g(x)_{min}=g(e^2)=\cfrac{1-lne^2}{(lne^2)^2}=\cfrac{1-2}{2^2}=-\cfrac{1}{4}\)，即\(a\leq -\cfrac{1}{4}\)。

反思：1、求函数\(g(x)\)的最小值时，这两个思路都是比较常用的，不过很明显二次函数法要简单一些。尽可能的防止不好的思维定式，不要一想到求最值就求导，当然求导是一种选择，不过是没有其他办法时的备选方法。

2、\(ln^2x\)的求导是复合函数的求导，容易出错。\((ln^2x)'=2lnx\cdot (lnx)'=2lnx\cdot \cfrac{1}{x}\).

(2). 若方程\((2x-m)lnx+x=0\)在区间\((1，e]\)上有两个不相等实根，求实数\(m\)的取值范围；

分析：这类题目往往需要分离参数，得到形如\(m=g(x)\)的形式，然后转化为函数有两个交点的问题，从而数形结合求解；

由题目分离参数，\(2x\cdot lnx-mlnx+x=0\)，变形整理为\(m=\cfrac{2xlnx+x}{lnx}=\cfrac{x}{lnx}+2x\)，

令\(h(x)=\cfrac{x}{lnx}+2x，x\in(1，e]\)，则往下的思路是想办法在同一个坐标系中做函数\(h(x)\)和函数\(y=m\)的图像，其中做函数\(h(x)\)的图像一般要用到导数方法，主要是涉及的函数比较复杂，一般方法不能处理。

则\(h’(x)=2+\cfrac{lnx-1}{ln^2x}=\cfrac{2ln^2x+lnx-1}{ln^2x}=\cfrac{(lnx+1)(2lnx-1)}{ln^2x}\)，

由于\(x>1\)，则\(lnx+1>0\)且\(ln^2x>0\)，故我们只需要解不等式\(2lnx-1>0(2lnx-1<0)\)就可以求得单调区间；

在这里我们自然还可以借助图像，做出导函数的部分函数的图像如右图，

由图可知，\(x\in (1，\sqrt{e}]\)时，\(2lnx-1<0\)，\(h'(x)<0\)，函数\(h(x)\)单调递减；

\(x\in [\sqrt{e}，e]\)时，\(2lnx-1>0\)，\(h'(x)>0\)，函数\(h(x)\)单调递增；

又\(h(\sqrt{e})=2\sqrt{e}+\cfrac{\sqrt{e}}{ln\sqrt{e}}=4\sqrt{e}\)；

\(h(e)=2e+\cfrac{e}{lne}=3e\)，其中\(x=1\)是函数\(h(x)\)的渐近线，如右图所示，

由图可知，实数\(m\)的取值范围为\(m\in (4\sqrt{e}，e]\)。

注意：1、函数\(h(x)\)的单调性的求法(一般题目复杂时常常首选导数法)；

2、注意函数图像的作图细节；

3、如果题目变成\(m=g(x)\)有解，则\(m\)的取值范围就是\(g(x)\)的值域，看看刚才的图形，这一点不需要我多解释了吧。

4、如果题目变成方程\(m=g(x)\)有\(n\)个解，那更需要数形结合来处理了；因为用代数的方法求解，只能处理简单的方程的情形，复杂一些的只能交给图形来直观观察了。

【2018宝鸡市高三数学第一次质量检测文理科第19题】已知四棱锥\(S-ABCD\)的底面为平行四边形，且\(SD\perp 面ABCD\)，\(AB=2AD=2SD\)，\(\angle DCB=60^{\circ}\)，\(M、N\)分别是\(SB、SC\)的中点，过\(MN\)作平面\(MNPQ\)分别与线段\(CD、AB\)相交于点\(P、Q\)。

(1).在图中作出平面\(MNPQ\)，使面\(MNPQ//面SAD\)(不要求证明)；

分析：如图所示，点\(P、Q\)分别是线段\(CD、AB\)的中点，联结\(NP、PQ、QM\)所得的平面即为所求做的平面。

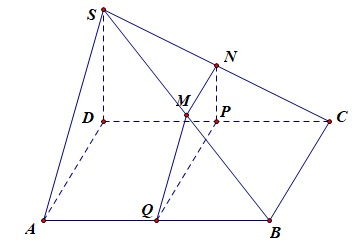
反思总结：1、一般的考法是题目作出这样的平面，然后要求我们证明面面平行，现在是要求我们利用面面平行的判定定理作出这样的平面，应该是要求提高了。

2、注意图中的线的虚实。

【文】若\(|\overrightarrow{AB}|=4\)，在(1)的条件下求多面体\(MNCBPQ\)的体积。

【文科】法1：

如图所示，连接\(PB、NB\)，有题目可知在(1)的情形下，平面\(MNPQ\)与平面\(ABCD\)垂直，有题目可知，

\(AB=4\)，\(BC=PC=2\)，\(SD=2\)，\(NP=1\)，

则\(SD\perp面ABCD\)，\(NP//SD\)，则\(NP\perp 面ABCD\)，

\(\Delta PCB\)是边长为2的等边三角形，则\(V_{N-PBC}=\cfrac{1}{3}\cdot S_{\Delta PBC}\cdot |NP|=\cfrac{1}{3}\cdot \cfrac{\sqrt{3}}{4}\cdot 4\cdot 1=\cfrac{\sqrt{3}}{3}\)

由\(MN//BC\)，\(MN \perp面SAD\)，面\(MNPQ\)是直角梯形，\(MN=NP=1\)，\(PQ=2\)

连接\(BD\)交\(PQ\)于点\(H\)，在\(\Delta ABD\)中，由余弦定理可知，\(BD=2\sqrt{3}\)，\(AB^2=AD^2+BD^2\)，则\(BD\perp AD\)

即\(BH\perp PQ\)，且\(BH\perp NP\)，故\(BH\perp 面MNPQ\)，

\(V_{B-MNPQ}=\cfrac{1}{3}\cdot S_{MNPQ}\cdot |BH|=\cfrac{1}{3}\cdot \cfrac{(1+2)\cdot 1}{2}\cdot \sqrt{3}=\cfrac{\sqrt{3}}{2}\)

故\(V_{MNCBPQ}=V_{B-MNPQ}+V_{N-PBC}=\cfrac{\sqrt{3}}{2}+\cfrac{\sqrt{3}}{3}=\cfrac{5\sqrt{3}}{6}\)。

法2：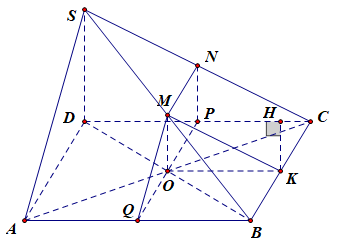

待补充。

【理】若\(\overrightarrow{AQ}=\lambda \overrightarrow{AB}\)，是否存在实数\(\lambda\)，使二面角\(M-PQ-B\)的平面角大小为\(60^{\circ}\)？若存在，求出\(\lambda\)的值；若不存在，请说明理由。

【理科】