正余弦定理

解三角形

三角形有三个角和三条边共6个元素，已知这6个元素中的一部分，求其余元素的过程就称为解三角形。

相关拓展

• 三角形内角和定理

\(A+B+C=\pi\)，\(\cfrac{A+B}{2}=\cfrac{\pi}{2}-\cfrac{C}{2}\)

• 三角形中的三角函数关系

\(sin(A+B)=sin(\pi-C)=sinC\)，

\(cos(A+B)=cos(\pi-C)=-cosC\)，

\(sin\cfrac{A+B}{2}=sin(\cfrac{\pi}{2}-\cfrac{C}{2})=cos\cfrac{C}{2}\)，

\(cos\cfrac{A+B}{2}=cos(\cfrac{\pi}{2}-\cfrac{C}{2})=sin\cfrac{C}{2}\)，

• 三角形中的射影定理

\(a=b\cdot cosC+c\cdot cosB\)，\(b=a\cdot cosC+c\cdot cosA\)，\(c=b\cdot cosA+a\cdot cosB\)，

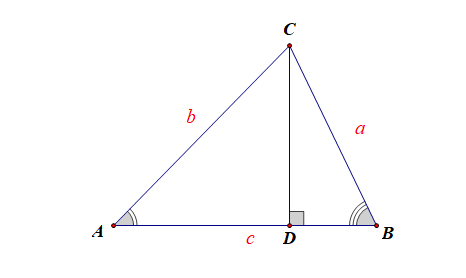
使用场景举例，如\(\cfrac{\sin^2A+\sin^2B-\sin^2C}{c}=\cfrac{\sin A\sin B}{a\cos B+b\cos A}\)，

即\(\cfrac{\sin^2A+\sin^2B-\sin^2C}{c}=\cfrac{\sin A\sin B}{c}\)，即\(a^2+b^2-c^2=ab\)；

正弦定理

1、定理的内容

• 文字语言：在一个三角形中，各边和它所对角的正弦的比相等；

• 符号语言：$$\cfrac{a}{sinA}=\cfrac{b}{sinB}=\cfrac{c}{sinC}$$

2、变形使用形式

边的形式：\(a=2RsinA\)，\(b=2RsinB\)，\(c=2Rsinc\)，

角的形式：\(sinA=\cfrac{a}{2R}\)，\(sinB=\cfrac{b}{2R}\)，\(sinC=\cfrac{c}{2R}\)，

比例形式：\(asinB=bsinA\)，\(asinC=csinA\)，\(bsinC=csinB\)，

连比形式：\(a:b:c=sinA:sinB:sinC\)；

\(\cfrac{a}{sinA}=\cfrac{b}{sinB}=\cfrac{c}{sinC}=\cfrac{a+b+c}{sinA+sinB+sinC}=2R\)

使用场景举例，如\(\cfrac{\sin A}{\sin B+\sin C}+\cfrac{b}{a+c}=1\)，

即\(\cfrac{a}{b+c}+\cfrac{b}{a+c}=1\)，整理得到，\(a^2+b^2-c^2=ab\)；

• 其他相关公式：

普通三角形的内切圆的半径\(r=\cfrac{2S}{a+b+c}(用割补法证明)\)，

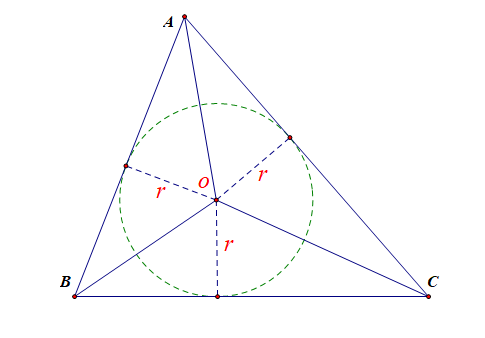
直角三角形的内切圆的半径\(r=\cfrac{1}{2}(a+b-c)(c为斜边)\)。

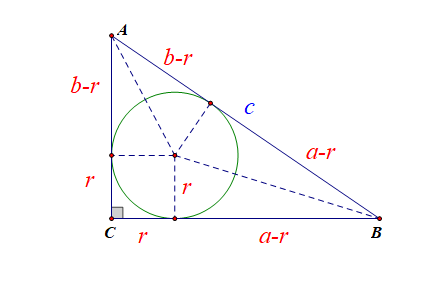
\(S_{\triangle ABC}=\cfrac{1}{2}\times a\times h_{a}=\cfrac{1}{2}\times r\times (a+b+c)\)

\(=\cfrac{1}{2}absinC=\cfrac{1}{2}bcsinA=\cfrac{1}{2}casinB=\cfrac{abc}{4R}\)

3、作用：从\(\cfrac{a}{sinA}=\cfrac{b}{sinB}=\cfrac{c}{sinC}\)分析；

①已知两角及任一边，求其余两边和另一角；

② 已知两边和其中一边的对角，求另一边的对角，进而求得其余的边和角。

在\(\Delta ABC\)中，已知\(a，b，A\)，三角形的解的个数这种情形比较复杂，见下表的动画演示：

• 情况总结如下，若感觉杂乱也不要紧，因为每一种形的形式都有唯一的数的形式对应，也就是说，通过计算就可以，当然，计算的时候还需要用到内角和定理，大边对大角，正余弦函数的图像和性质。

	$A$ 为钝角	$A$ 为直角	$A$ 为锐角
$a$$\;$$>$$\;$$b$	一解	一解	一解
$a$$\;$$=$$\;$$b$	无解	无解	一解
$a$$\;$$<$$\;$$b$	无解	无解	$a$$\;$$>$$\;$$b$$\cdot$$\sin$$A$	两解
			$a$$\;$$>$$\;$$b$$\cdot$$\sin$$A$	一解
			$a$$\;$$<$$\;$$b$$\cdot$$\sin$$A$	无解

余弦定理

1、定理的内容

• 文字语言：三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。

• 符号语言：

\[a^2=b^2+c^2-2bccosA \]

\[b^2=c^2+a^2-2cacosB \]

\[c^2=a^2+b^2-2abcosC \]

当\(A=\cfrac{\pi}{2}\)时，余弦定理变形为\(a^2=b^2+c^2\)，即勾股定理，故我们说勾股定理时余弦定理的特殊情形。

角的形式：

\(cosA=\cfrac{b^2+c^2-a^2}{2bc}\)；\(cosB=\cfrac{a^2+c^2-b^2}{2ac}\)；\(cosC=\cfrac{a^2+b^2-c^2}{2ab}\)；

2、变形使用形式

\(b^2+c^2-a^2=2bccosA\)；\(a^2-b^2-c^2=-2bccosA\)；

\(sin^2C+sin^2A-sin^2B=2\sin A\cdot\sin C\cdot\cos B\)；

\(cosB=\cfrac{a^2+c^2-b^2}{2ac}=\cfrac{sin^2C+sin^2A-sin^2B}{2sinAsinC}\)；

3、作用

①已知两边及夹角，求第三边，进而求其余两角。

②已知三边，求三个内角。

在使用余弦定理时，我们的思维大多习惯于已知两边及其夹角，求第三边，如图一所示，已知边\(a、c\)和角\(B\)，求第三边\(b\)，此时相当于求函数值一样的简单和容易。有时候当已知两边及一边的对角求第三边时，我们往往就会忘记用余弦定理而转用正弦定理，这样就费事了，其实此时还可以用余弦定理直接求第三边。如图二所示，已知边\(a、b\)和角\(B\)，求第三边\(c\)，我们可以这样\(b^2=a^2+c^2-2accosB\)，转求关于\(c\)的方程即可。

某观测站\(C\) 在城\(A\) 的南偏西\(20°\)的方向上，由城\(A\)出发的一条公路，走向是南偏东\(40°\)，在\(C\)处测得公路上距\(C\)点\(31\)km的\(B\)处有一人正沿公路向城\(A\)走去，走了\(20\)km后到达\(D\)处，此时\(C\)，\(D\)间的距离为\(21\)km，这人还要走多远才能到达城 \(A\)?

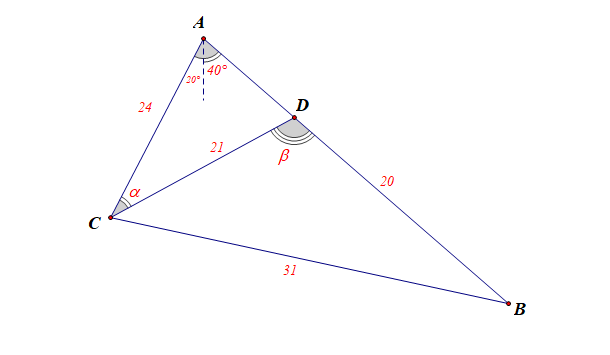
【错解】如图所示，\(\angle CAD=60^{\circ}\)，

在\(\triangle BCD\)，由余弦定理， 得\(\cos B=\cfrac{BC^2+BD^2-CD^2}{2\cdot BC\cdot BD}\)\(=\cfrac{31^{2}+20^{2}-21^{2}}{2\times 31\times 20}=\cfrac{23}{31}\)，

所以 \(\sin B=\sqrt{1-\cos^2B}=\cfrac{12\sqrt{3}}{31}\).

在 \(\triangle ABC\)中， 由正弦定理得到\(AC=\cfrac{BC\cdot \sin B}{\sin\angle CAB}=24\) (km)

在\(\triangle ACD\)，由余弦定理，

得 \(CD^2=AC^2+AD^2-2AC\cdot AD\cos\angle CAD\)，

即 \(21^{2}=24^{2}+AD^{2}-24\cdot AD\)，

所以 \(AD=15\) (km) 或 \(AD=9\) (km) ，

所以这人还要走 \(15\)或\(9\) 才能到达城\(A\)。

[错因分析]

1.从生活经验来判断，这个结论显然有些荒谬，从图中看，点\(A\)，\(D\)，\(B\)三点共线，\(AD\)应该为直线段，故只应该有一个解；

2.从数的角度分析，在余弦定理中，线段的长度都带有平方，故求线段的长度时可能会有两个值，若出现一正一负根时，容易排除，但出现两个正根时，排除增根就不大容易了；

【正解】 设\(\angle ACD=\alpha\)，\(\angle CDB=\beta\),

在 \(\triangle CBD\)中，由余弦定理， 得\(\cos\beta=\cfrac{BD^2+CD^2-CB^2}{2BD\cdot CD}\)

\(=\cfrac{20^{2}+21^{2}-31^{2}}{2\times 20\times 21}=-\cfrac{1}{7}\)，

所以 \(\sin\beta=\cfrac{4\sqrt{3}}{7}\)；

而 \(\sin\alpha=\sin(\beta-60^{\circ})=\sin\beta\cos60^{\circ}-\cos\beta\sin 60^{\circ}\)，

\(=\cfrac{4\sqrt{3}}{7} \times \cfrac{1}{2}+\cfrac{\sqrt{3}}{2} \times \cfrac{1}{7}=\cfrac{5\sqrt{3}}{14}\)，

在 \(\triangle ACD\)中，由正弦定理，得\(\cfrac{CD}{\sin60^{\circ}}=\cfrac{AD}{\sin\alpha}\)，

则 \(AD=\cfrac{21\times\sin\alpha}{\sin60^{\circ}}=15\)(km)

所以这人还要走 \(15\) kmオ能到达城 \(A\).

[如何排除错误] 由\(\sin\beta=\cfrac{4\sqrt{3}}{7}\)，得到\(\cos \alpha=\pm\cfrac{11}{14}\)，

当\(\cos\alpha=\cfrac{11}{14}>\cfrac{1}{2}\)时，\(\alpha\in (0,\cfrac{\pi}{3})\)，此时由余弦定理的边的形式

得到\(AD^2=AC^2+CD^2-2\cdot AC\cdot CD=225\)，故\(AD=15\)；

当\(\cos\alpha=-\cfrac{11}{14}<-\cfrac{1}{2}\)时，\(\alpha\in (\cfrac{2\pi}{3},\pi)\)，此时\(\beta=\alpha+\cfrac{\pi}{3}>\pi\)，不符合题意，舍去。

故仅有一个根\(AD=15\)；

正余弦定理与三角形全等判定方法的关系

我们在初中学习知道，\(SSS\)、\(SAS\)、\(ASA\)、\(AAS\)、\(HL\) 这些定理都可以判断三角形全等，学习了正余弦定理之后，就能从数的角度解释原因了。比如 \(SAS\)，即已知两边及其夹角的边角边定理，由余弦定理，可以求得第三边，只有一解，故这样的三角形是唯一的，那么满足这样条件的两个三角形只能是全等关系，而 \(SSA\) 是不能作为三角形全等的判定方法的，原因是已知两边及其一边的对角，求得得到的三角形可能有一解，两解或者无解的情形，故不能作为三角形全等的判定方法。引例如图，两个三角形 \(\triangle ACB_1\) 和 \(\triangle ACB_2\) 满足 \(AC=AC\)， \(CB_1=CB_2\)，且 \(\angle CAB_1=\angle CAB_2\)，即满足条件 边边角，但是很显然，这两个三角形不全等。

典例剖析

【2019届宝鸡市高三理科数学质检Ⅰ第7题】\(\triangle ABC\)的内角\(A，B，C\)所对的边分别为\(a，b，c\)，已知\(b=\sqrt{7}\)，\(c=4\)，\(cosB=\cfrac{3}{4}\)，则\(\Delta ABC\)的面积为【\(\qquad\)】

$A.3\sqrt{7}$ $B.\cfrac{3\sqrt{7}}{2}$ $C.9$ $D.\cfrac{9}{2}$

分析：属于三角函数中已知两边和一边的对角的形式，常用正弦定理或余弦定理求解；

更多的采用余弦定理的方程表达形式，也是考试中对余弦定理考察形式中的高频考查模式。

\(b^2=a^2+c^2-2accosB\)，即\(7=a^2+14-2a\times 4\times\cfrac{3}{4}\)，

得到\(a^2-6a+9=0\)，即\(a=3\)，又由于\(sinB=\cfrac{\sqrt{7}}{4}\)，

故\(S_{\Delta ABC}=\cfrac{1}{2}acsinB=\cfrac{3\sqrt{7}}{2}\)，选\(B\)。

【2016天津高考】在\(\Delta ABC\)中，\(AB=\sqrt{13}\)，\(BC=3\)，\(\angle C=120^{\circ}\)，则\(AC\)=【\(\qquad\)】

$A、1$ $B、2$ $C、3$ $D、4$

分析：本题目已知\(c=AB=\sqrt{13}\)，\(a=BC=3\)，\(\angle C=120^{\circ}\)，

即已知两边及一边的对角，求第三边\(AC=b=?\)；

求解思路可以用正弦定理，也可以用余弦定理，不过使用余弦定理一次就能到位。

由\(c^2=a^2+b^2-2abcosC\)，代值得到\(13=9+b^2-2\times 3\times b\times (-\cfrac{1}{2})\)；

化简得到\(b^2+3b-4=0\)，解得\(b=1\)或\(b=-4\)(舍负)，故\(AC=1\)，选\(A\)。

反思：在具体题目中到底应该选正弦定理还是余弦定理来解三角形，应该具体分析，当然还需要我们搞清楚这两个定理能解决的基本类型，以便于更好的使用。

【2020届高三数学资料题】已知\(\triangle ABC\)的内角\(A，B，C\)所对的边分别为\(a，b，c\)，且\(\frac{c-b}{c-a}=\)\(\frac{sinA}{sinC+sinB}\)，则\(B\)等于【\(\qquad\)】

$A.\cfrac{\pi}{6}$ $B.\cfrac{\pi}{4}$ $C.\cfrac{\pi}{3}$ $D.\cfrac{3\pi}{4}$

法1：角化边，\(\cfrac{c-b}{c-a}=\)\(\cfrac{sinA}{sinC+sinB}=\cfrac{a}{c+b}\)，

整理得到\(a^2+c^2-b^2=ac\)，代入\(cosB=\cfrac{a^2+c^2-b^2}{2ac}=\cfrac{1}{2}\)，

由\(B\in (0，\pi)\)，则\(B=\cfrac{\pi}{3}\)，故选\(C\)。

法2：边化角，由\(\cfrac{c-b}{c-a}=\)\(\cfrac{sinA}{sinC+sinB}\)，

得到\(\cfrac{sinC-sinB}{sinC-sinA}=\)\(\cfrac{sinA}{sinC+sinB}\)，

整理得到\(sin^2C-sin^2B=sinC sinA-sin^2A\)，

即\(sin^2C+sin^2A-sin^2B=sinC sinA\)，

整理得到\(a^2+c^2-b^2=ac\)，代入\(cosB=\cfrac{a^2+c^2-b^2}{2ac}=\cfrac{1}{2}\)，

由\(B\in (0，\pi)\)，则\(B=\cfrac{\pi}{3}\)，故选\(C\)。

【2018\(\cdot\)浙江卷】已知\(\triangle ABC\)的内角\(A，B，C\)所对的边分别为\(a，b，c\)，若\(a=\sqrt{7}\)，\(b=2\)， \(A=60^{\circ}\)， 则 \(\sin B\)=__________ \(c=\)__________.

解析: (1) 由正弦定理\(\cfrac{a}{\sin A}=\cfrac{b}{\sin B}\)，

得\(\sin B=\cfrac{b}{a}\cdot\sin A=\cfrac{2}{\sqrt{7}}\times\cfrac{\sqrt{3}}{2}=\cfrac{\sqrt{21}}{7}\)

(2) 由余弦定理\(a^{2}=b^{2}+c^{2}-2bc\cdot\cos A\)， 得\(7=4+c^2-4c\times\cos 60^{\circ}\)，

即 \(c^{2}-2c-3=0\)， 解得 \(c=3\) 或 \(c=-1\)( 舍去 ). \(\quad\)故答案 \(\cfrac{\sqrt{21}}{7}\)；\(3\)

在 \(\triangle ABC\)中，角 \(A\)， \(B\)， \(C\) 所对的边长分别为 \(a\)、 \(b\)、 \(c\)， \(\sin A\)、 \(\sin B\)、\(\sin C\)成等比数列， 且\(c=2a\)，则\(\cos B\) 的值为 【\(\qquad\)】

$A.\cfrac{1}{4}$ $B.\cfrac{3}{4}$ $C.\cfrac{\sqrt{2}}{4}$ $D.\cfrac{\sqrt{2}}{3}$

解析: 因为 \(\sin A\)， \(\sin B\)， \(\sin C\) 成等比数列， 所以 \(\sin^{2} B=\sin A \sin C\)，

由正弦定理得 \(b^{2}=ac\)，又 \(c=2a\)，故\(\cos B=\cfrac{a^{2}+c^{2}-b^{2}}{2ac}=\cfrac{a^{2}+4a^{2}-2 a^{2}}{4a^{2}}=\cfrac{3}{4}\)，故选\(B\).

补充：若要求解\(\sin B\)，则\(\sin B=\cfrac{\sqrt{7}}{4}\)；

【2019\(\cdot\)合肥质检】\(\triangle ABC\) 的内角\(A\)， \(B\)， \(C\) 所对的边长分别为 \(a\)、 \(b\)、 \(c\)，若 \(\cos C\)\(=\)\(\cfrac{2\sqrt{2}}{3}\)， \(b\cos A\)\(+\)\(a\cos B\)\(=\)\(2\)，则\(\triangle\)\(ABC\) 的外接圆面积为 【\(\qquad\)】

$A.4\pi$ $B.8 \pi$ $C.9\pi$ $D.36\pi$

解：设\(\triangle ABC\) 的外接圆的半径为 \(R\)， 由射影定理得到，\(c=b\cos A+a\cos B=2\)，

又由\(\cos C=\cfrac{2\sqrt{2}}{3}\)，解得\(\sin C=\cfrac{1}{3}\)，

则由正弦定理可得 \(2R=\cfrac{c}{\sin C}=\cfrac{2}{\frac{1}{3}}=6\)，

故解得\(R=3\)，则外接圆的面积为 \(S=\pi R^{2}=9\pi\)，故选 \(C\).

【2020\(\cdot\)高三学生训练题】如图所示，为了测量某湖泊两侧\(A\)，\(B\)间的距离，李宁同学首先选定了与\(A\)，\(B\)不共线的一点\(C\)(\(△ABC\)的角\(A\)，\(B\)，\(C\)所对的边分别记为\(a\)，\(b\)，\(c\))，然后给出了三种测量方案：①测量\(A\)，\(C\)，\(b\)；②测量\(a\)，\(b\)，\(C\)；③测量\(A\)，\(B\)，\(a\).则一定能确定\(A\)，\(B\)间的距离的所有方案的序号为【\(\qquad\)】

$A.①②$ $B.②③$ $C.①③$ $D.①②③$

解析：对于①③可以利用正弦定理确定唯一的\(A\)，\(B\)两点间的距离，对于②直接利用余弦定理即可确定\(A\)，\(B\)两点间的距离，故选 \(D\).