用导数研究函数的性质
用导数研究函数的性质
前言
典例剖析
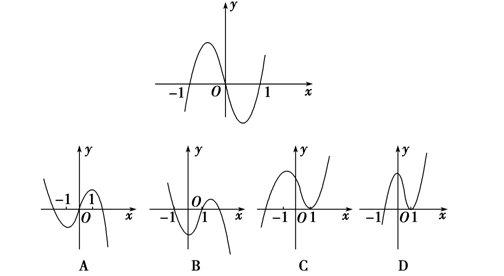
分析：由图可知，当\(x<-1\)时，\(y<0\)，故由符号法则可知\(f'(x)>0\)；
当\(-1<x<0\)时，\(y>0\)，故由符号法则可知\(f'(x)<0\)；
当\(0<x<1\)时，\(y<0\)，故由符号法则可知\(f'(x)<0\)；
当\(x>1\)时，\(y>0\)，故由符号法则可知\(f'(x)>0\)；
从而可知当\(x<-1\)时，\(f'(x)>0\)，\(f(x)\nearrow\)；
当\(-1<x<1\)时，\(f'(x)<0\)，\(f(x)\searrow\)；当\(x>1\)时，\(f'(x)>0\)，\(f(x)\nearrow\)；故选\(C\)。
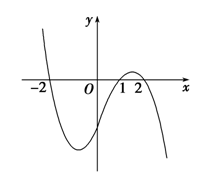
分析：当\(x<-2\)时，则有\(1-x>0\)，又\(y>0\)，故由符号法则可知\(f'(x)>0\)；
当\(-2<x<1\)时，则有\(1-x>0\)，又\(y<0\)，故由符号法则可知\(f'(x)<0\)；
当\(1<x<2\)时，则有\(1-x<0\)，又\(y>0\)，故由符号法则可知\(f'(x)<0\)；
当\(x>2\)时，则有\(1-x<0\)，又\(y<0\)，故由符号法则可知\(f'(x)>0\)；
从而可知当\(x<-2\)时，\(f'(x)>0\)，\(f(x)\nearrow\)；
当\(-2<x<2\)时，\(f'(x)<0\)，\(f(x)\searrow\)；
当\(x>2\)时，\(f'(x)>0\)，\(f(x)\nearrow\)；故选\(D\)。
分析：\(f'(x)=m(e^{mx}-1)+2x\)，将函数\(y_1=m(e^{mx}-1)\)和\(y_2=2x\)的图像画在同一个坐标系中，如右图所示，
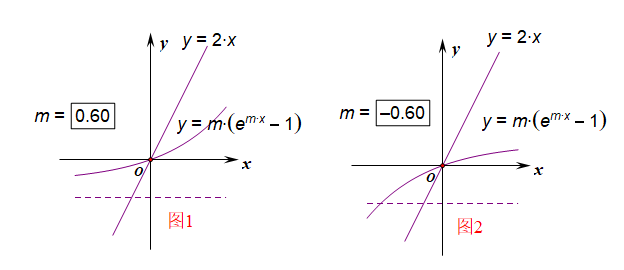
当\(m\ge 0\)时，\(x\in(-\infty，0)\)，\(m(e^{mx}-1)<0\)，\(2x<0\)，则\(f'(x)<0\)；\(x\in(0，+\infty)\)，\(m(e^{mx}-1)>0\)，\(2x>0\)，则\(f'(x)>0\)；
当\(m< 0\)时，\(x\in(-\infty，0)\)，\(m(e^{mx}-1)<0\)，\(2x<0\)，则\(f'(x)<0\)；\(x\in(0，+\infty)\)，\(m(e^{mx}-1)>0\)，\(2x>0\)，则\(f'(x)>0\)；
综上所述，函数\(f(x)\)在 \((-\infty，0)\)上单调递减，在\((0，+\infty)\)上单调递增。
引申：加减乘除？
分析：先求函数的定义域为\(R\)，\(f'(x)=3x^2+2ax=\cfrac{1}{3}x(x+\cfrac{2a}{3})\)，令\(f'(x)=0\)，得到\(x=0\)或\(x=-\cfrac{2a}{3}\)，
针对两个根的大小分类讨论如下
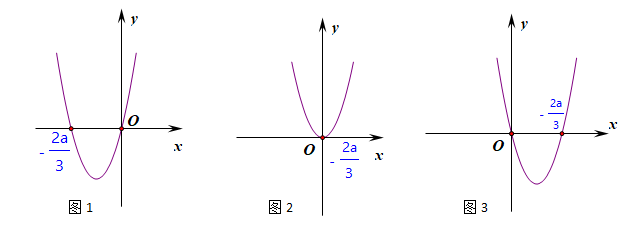
当\(a>0\)时，如图1所示，当\(x<-\cfrac{2a}{3}\)或\(x>0\)时，\(f'(x)>0\)；当\(-\cfrac{2a}{3}<x<0\)时，\(f'(x)<0\)；
当\(a=0\)时，如图2所示，\(f'(x)\ge 0\)恒成立，且仅仅在\(x=0\)一个点处取到0；
当\(a<0\)时，如图3所示，当\(x<0\)或\(x>-\cfrac{2a}{3}\)时，\(f'(x)>0\)；当\(0<x<-\cfrac{2a}{3}\)时，\(f'(x)<0\)；
综上所述，当\(a<0\)时，函数\(f(x)\)的单调递增区间是\((-\infty，0)\)和\((-\cfrac{2a}{3}，+\infty)\)，单调递减区间是\((0，-\cfrac{2a}{3})\)；
当\(a=0\)时，函数\(f(x)\)的单调递增区间是\((-\infty，+\infty)\)；
当\(a>0\)时，函数\(f(x)\)的单调递增区间是\((-\infty，-\cfrac{2a}{3})\)和\((0，+\infty)\)，单调递减区间是\((-\cfrac{2a}{3}，0)\)；
(1).讨论函数\(f(x)\)的单调性；
分析：用导数法求解，\(f'(x)=3x^2-a\) ，作出导函数的简图(三种代表情形)，
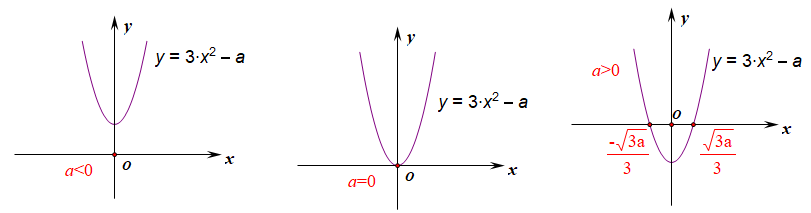
当\(a\leq 0\)时，\(f'(x)\ge 0\)，故在\((-\infty，+\infty)\)上单调递增；
当\(a>0\)时，令\(f'(x)=0\)，得到\(x=\pm \cfrac{\sqrt{3a}}{3}\)，故\(x\in (-\infty， -\cfrac{\sqrt{3a}}{3})\)时，\(f'(x)>0\)，\(f(x)\nearrow\)；
\(x\in (-\cfrac{\sqrt{3a}}{3}，\cfrac{\sqrt{3a}}{3})\)时，\(f'(x)<0\)，\(f(x)\searrow\)；\(x\in (\cfrac{\sqrt{3a}}{3}，+\infty)\)时，\(f'(x)>0\)，\(f(x)\nearrow\)；
(2).若函数\(f(x)\)在\(R\)上是增函数，求\(a\)的取值范围。
分析：由于函数\(f(x)\)在\(R\)上是增函数，即\(f'(x)\geqslant 0\)在\(R\)上恒成立，且满足不恒\(f'(x)=0\)，即\(f(x)\)不为常函数；
则\(f'(x)=3x^2-a\geqslant 0\)恒成立，分离参数得到，
\(a\leqslant 3x^2\)在\(R\)上恒成立，而\((3x^2)_{min}=0\)，
则\(a\leqslant 0\)，又因为当\(a=0\)时，函数不为常函数，故参数\(a\)的取值范围是\(a\in (-\infty,0]\)。
分析： \(f'(x)=3x^2-a\ge 0\)在\((1，+\infty)\)上恒成立，故\(a\leq 3x^2\)在\((1，+\infty)\)上恒成立，
需要求\(y=3x^2\)在\((1，+\infty)\)上的最小值或者最小值极限为\(3\)，故有\(a\leq 3\)；
分析： \(f'(x)=3x^2-a\leq 0\)在\((-1，1)\)上恒成立，
故\(a\ge 3x^2\)在\((-1，1)\)上恒成立，
需要求\(y=3x^2\)在\((-1，1)\)上的最大值或者最大值极限为\(3\)，故有\(a\ge 3\)；
分析：由第一问可知函数在\((-\cfrac{\sqrt{3a}}{3}，\cfrac{\sqrt{3a}}{3})\)上单调递减，
现已知单调递减区间是\((-1，1)\)，故这两个区间相等，
即\(\cfrac{\sqrt{3a}}{3}=1\)，解得\(a=3\)；
法1：补集思想，由上述解题过程可知
当单增时，\(a\leq 0\)；当单减时，\(a\ge 3\)，故其补集则\(0<a<3\)时必然不单调。
故\(a\)的取值范围为\(a\in (0，3)\)。
法2： 函数\(f(x)\)在区间\((-1，1)\)上有增有减，即函数\(y=f'(x)\)在\((-1，1)\)上至少有一个变号零点，
当有一个变号零点时，\(f'(-1)\cdot f'(1)<0\)，解得\(a\in \varnothing\)；
当有两个变号零点时，结合函数\(f'(x)=3x^2-a\)的图像的对称性可知，
转化为函数\(y=f'(x)\)在\((0，1)\)上有一个变号零点，故\(f'(0)\cdot f'(1)<0\)，
解得\(0<a<3\)。
综上可知，\(0<a<3\)。
法1：补集思想，\(f'(x)=x^2-2x+a\)，
若函数\(f(x)\)在\([-1，2]\)上单增，则\(f'(x)=x^2-2x+a\ge 0\)恒成立，
分离参数得到\(a\ge -x^2+2x\)恒成立，
在\([-1，2]\)上求得函数\(f(x)_{max}=1\)，故\(a\ge 1\)；
若函数\(f(x)\)在\([-1，2]\)上单减，则\(f'(x)=x^2-2x+a\leq 0\)恒成立，
分离参数得到\(a\leq -x^2+2x\)恒成立，
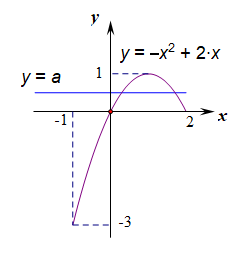
在\([-1，2]\)上求得函数\(f(x)_{min}=-3\)，故\(a\leq -3\)；
故取其补集，当\(-3<a<1\)时，函数\(f(x)\)在区间\([-1，2]\)上不单调。
法2：由题可知\(f(x)\)不单调，则导函数\(y=f'(x)\)在区间\([-1，2]\)上至少有一个变号零点，
当只有一个变号零点时，由\(f'(-1)\cdot f'(2)\leq 0\)可得，\(-3\leq a\leq 0\)；
当有两个变号零点时，由\(\begin{cases}f'(-1)>0\\f'(2)>0\\\Delta >0\end{cases}\)，解得\(0<a<1\)；
综上所述，实数\(a\)的取值范围是\((-3，1)\)。
法3：(转化为方程有解类型求解)由法2可知，导函数\(y=f'(x)\)在区间\([-1，2]\)上至少有一个变号零点，
即方程\(f'(x)=0\)至少有一个解，故\(a=-x^2+2x\)在\([-1，2]\)上至少有一个解，
到此转化为方程有解类型，
需要求出函数\(y=-x^2+2x，x\in [-1，2]\)上的值域\([-3，1]\)，
由于上述的转化过程不是等价的，故需要检验。
当\(a=-3\)时，\(f'(x)=x^2-2x-3=(x+1)(x-3)\)，此时若\(x\in [-1，2]\)，
则有\(f'(x)\leq 0\)恒成立，故函数\(f(x)\)在区间\([-1，2]\)上单调递减，
不符合题意，舍去；
当\(a=1\)时，\(f'(x)=x^2-2x+1=(x-1)^2\)，此时若\(x\in [-1，2]\)，
则有\(f'(x)\ge 0\)恒成立，故函数\(f(x)\)在区间\([-1，2]\)上单调递增，
不符合题意，舍去；
故实数\(a\)的取值范围是\((-3，1)\)。
法1：分类讨论法，\(f'(x)=x^2-2x+a\)，
若函数\(f(x)\)在\([-1，2]\)上单增，则\(f'(x)=x^2-2x+a\ge 0\)恒成立，
分离参数得到\(a\ge -x^2+2x\)恒成立，
在\([-1，2]\)上求得函数\(f(x)_{max}=1\)，故\(a\ge 1\)；
若函数\(f(x)\)在\([-1，2]\)上单减，则\(f'(x)=x^2-2x+a\leq 0\)恒成立，
分离参数得到\(a\leq -x^2+2x\)恒成立，
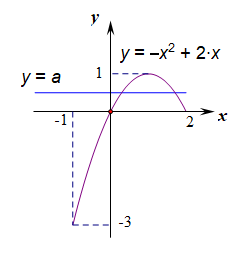
在\([-1，2]\)上求得函数\(f(x)_{min}=-3\)，故\(a\leq -3\)；
故当\(a\in (-\infty，-3]\cup[1，+\infty)\)时，函数\(f(x)\)在区间\([-1，2]\)上单调。
法2：直接法，由于函数\(f(x)=\cfrac{1}{3}x^3-x^2+ax-5\)在区间\([-1，2]\)上单调，
则函数\(y=f'(x)\)在区间\([1，2]\)上无零点，
即方程\(f'(x)=x^2-2x+a=0\)在区间\([1，2]\)上无解，
即方程\(a=-x^2+2x\)在区间\([1，2]\)上无解，
由图像可知，\(f'(x)\)的值域为\([-3，1]\)，故
\(a<-3\)或\(a>1\)，
由于上述的转化是不等价的，以下检验端点值是否满足题意。
当\(a=-3\)时，\(f'(x)=x^2-2x-3=(x+1)(x-3)\)，此时若\(x\in [-1，2]\)，
则有\(f'(x)\leq 0\)恒成立，故函数\(f(x)\)在区间\([-1，2]\)上单调递减，
符合题意，添加\(a=-3\)；
当\(a=1\)时，\(f'(x)=x^2-2x+1=(x-1)^2\)，此时若\(x\in [-1，2]\)，
则有\(f'(x)\ge 0\)恒成立，故函数\(f(x)\)在区间\([-1，2]\)上单调递增，
符合题意，添加\(a=1\)；
综上所述，函数\(f(x)=\cfrac{1}{3}x^3-x^2+ax-5\)在区间\([-1，2]\)上单调，
则实数\(a\)的取值范围是\(a\in (-\infty，-3]\cup[1，+\infty)\)。
分析：定义域为\((0，+\infty)\)，\(f'(x)=a-\cfrac{1}{x}=\cfrac{ax-1}{x}\)，如右图所示，借助分子的图像，分类讨论如下
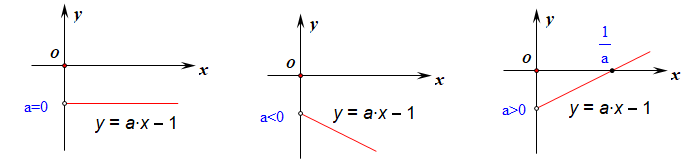
当\(a\leq 0\)时，\(f'(x)<0\)，则\(f(x)\)单调递减，故函数\(f(x)\)无极值；
当\(a>0\)时，令\(f'(x)=0\)，得到\(x=\cfrac{1}{a}\) ，
则\(x\in (0，\cfrac{1}{a})\)，\(f'(x)<0\)，则\(f(x)\)单调递减，
\(x\in (\cfrac{1}{a}，+\infty)\)，\(f'(x)>0\)，则\(f(x)\)单调递增，
故当\(x=\cfrac{1}{a}\)时，\(f(x)_{极小值}=f(a)=lna\)，无极大值。
分析：\(f(x)=\cfrac{1}{x}-1+klnx\)，则\(f'(x)=-\cfrac{1}{x^2}+\cfrac{k}{x}=\cfrac{kx-1}{x^2}\)，
作出分子函数的各种可能的图像(只需要观察图中的夹在两条平行线之间的蓝色线段的正负即可)，分类讨论如下：
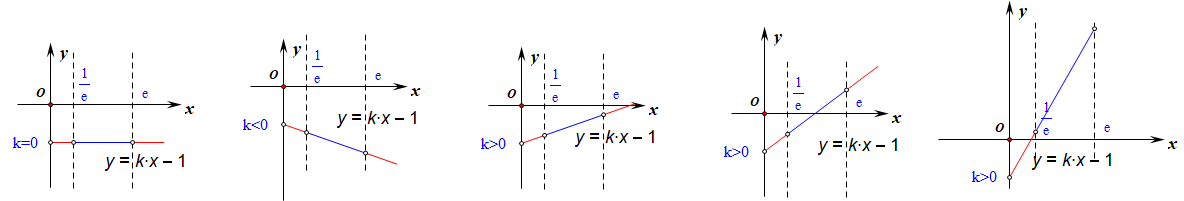
当\(k\leq 0\)时，\(f'(x)<0\)，\(f(x)\)单调递减，故\(f(x)_{min}=f(e)=\cfrac{1}{e}-1+k\)，\(f(x)_{max}=f(\cfrac{1}{e})=e-1-k\)；
当\(0<k<\cfrac{1}{e}\)时，令\(f'(x)=0\)，得到\(x=\cfrac{1}{k}\)，则\(\cfrac{1}{k}>e\)，\(f'(x)<0\)，\(f(x)\)单调递减，故\(f(x)_{min}=f(e)=\cfrac{1}{e}-1+k\)，\(f(x)_{max}=f(\cfrac{1}{e})=e-1-k\)；
综上所述，函数\(f(x)\)在\([\cfrac{1}{e}，e]\)上的最大值和最小值\(f(x)_{min}=f(e)=\cfrac{1}{e}-1+k\)，\(f(x)_{max}=f(\cfrac{1}{e})=e-1-k\)。
反思总结：若题目没有限制\(k\)的取值，那么就还会用到后边的两个图像了。
分析：若是\(R\)上的单调递减函数，则\(f'(x)\leq 0\)恒成立，
现在不是\(R\)上的单调递减函数，
故\(f'(x)=-x^2+2bx-2b-3=-(x-b)^2+b^2-2b-3>0\)在R上能成立，
故只需要\(f'(x)_{max}=b^2-2b-3>0\)即可，
解得\(b<-1\)或\(b>3\)。故\(b\in (-\infty，-1)\cup(3，+\infty)\)。
反思总结：不是单调递减的情形可能包含有单调递增函数或常函数或有增有减函数。
法1：由于函数\(f(x)\)在\([\cfrac{2}{3}，+\infty)\)上存在单调递增区间，
说明在此区间上，\(f'(x)> 0\)在\([\cfrac{2}{3}，+\infty)\)上能成立，
即\(f'(x)=-x^2+x+2a> 0\)在\([\cfrac{2}{3}，+\infty)\)上能成立，
即\(2a>x^2-x=(x-\cfrac{1}{2})^2-\cfrac{1}{4}=g(x)\)在\([\cfrac{2}{3}，+\infty)\)上能成立，
而函数\(g(x)_{min}=g(\cfrac{2}{3})=-\cfrac{2}{9}\)，
故\(2a>-\cfrac{2}{9}\)，即\(a>-\cfrac{1}{9}\)，
反思总结：本题目若转化为\(f'(x)\ge 0\)在\([\cfrac{2}{3}，+\infty)\)上能成立，则最后参数的值会多出\(a=-\cfrac{1}{9}\)，
所以务必要注意转化的等价性，或者说我们还需要注意导函数\(f'(x)\)的具体形式。
法2：由于函数\(f(x)\)在\([\cfrac{2}{3}，+\infty)\)上存在单调递增区间，
说明在此区间上，\(f'(x)> 0\)在\([\cfrac{2}{3}，+\infty)\)上能成立，
即\(f'(x)=-x^2+x+2a> 0\)在\([\cfrac{2}{3}，+\infty)\)上能成立，
\(f'(x)=-x^2+x+2a=-(x-\cfrac{1}{2})^2+\cfrac{1}{4}+2a\)，
当\(x\in [\cfrac{2}{3}，+\infty)\) 时，\(f'(x)_{max}=f'(\cfrac{2}{3})=\cfrac{2}{9}+2a\)。
令\(\cfrac{2}{9}+2a>0\)，
解得\(a>-\cfrac{1}{9}\)，所以\(a\)的取值范围是\((-\cfrac{1}{9}，+\infty)\)。
分析：函数\(f(x)=x^2-4e^x-ax\)在\(R\)上存在单调递增区间，
则\(f'(x)=2x-4e^x-a> 0\)在\(R\)上有解，
即\(a> 2x-4e^x\)在\(R\)上有解，
令\(g(x)=2x-4e^x\)，则\(g'(x)=2-4e^x\) ，
当\(x<-ln2\)时，\(g'(x)>0\)；当\(x>-ln2\)时，\(g'(x)<0\)；
故\(g(x)_{max}=g(-ln2)=-2ln2-2\)
故实数\(a\)的取值范围是\((-\infty，-2ln2-2)\)。
分析：函数\(f(x)=lnx+(x-a)^2(a\in R)\)在区间\([\cfrac{1}{2}，2]\)上存在单调递增区间，
则函数\(f(x)\)在区间\([\cfrac{1}{2}，2]\)上存在子区间使得\(f'(x)> 0\)能成立，
\(f'(x)=\cfrac{1}{x}+2x-2a=\cfrac{2x^2-2ax+1}{x}> 0\)；
令\(h(x)=2x^2-2ax+1\) ，
法1：接上，要使\(f'(x)> 0\)，则有\(h(2)> 0\) 或\(h(\cfrac{1}{2})> 0\)，
解得\(a< \cfrac{9}{4}\)，故实数\(a\)的取值范围是\((-\infty，\cfrac{9}{4})\)。
法2：正难则反，要使\(f'(x)\leq 0\)，则在区间\([\cfrac{1}{2}，2]\)上，\(h(x)\leq 0\) ，
即\(\begin{cases}h(\cfrac{1}{2})\leq 0\\h(2)\leq 0\end{cases}\)，解得\(a\ge \cfrac{9}{4}\)，
故实数\(a\)的取值范围是\((-\infty，\cfrac{9}{4})\)。
反思：本题目为什么不能是\(f'(x)\ge 0\)? 见高频易错题目。
分析：\(f'(x)=x^2+ax+a+3\)，函数\(f(x)\)在\(R\)上不是单调函数，
则\(f'(x)=0\)有两个不等实根，即\(\Delta =a^2-4(a+3)>0\)，解得\(a<-2\)或\(a>6\)。
分析：由题目可知，\(f'(x)\ge 0\)在区间\([\cfrac{1}{2}，4]\)上恒成立，
\(f'(x)=(2x-c)e^x+(x^2-cx+5)e^x=(x^2-cx+2x-c+5)e^x\ge 0\)，
即\(x^2-cx+2x-c+5\ge 0\)，分离参数得到，
即\(cx+c\leq x^2+2x+5\)在区间\([\cfrac{1}{2}，4]\)上恒成立，
即\(c\leq \cfrac{x^2+2x+5}{x+1}\)在区间\([\cfrac{1}{2}，4]\)上恒成立，
令\(h(x)= \cfrac{x^2+2x+5}{x+1}= \cfrac{x^2+2x+1+4}{x+1}=x+1+\cfrac{4}{x+1}\ge 2\sqrt{4}=4\)，
当且仅当\(x+1=\cfrac{4}{x+1}\)，即\(x=1\in [\cfrac{1}{2}，4]\)时取到等号；
故\(c\leq 4\)，故选\(B\)。
