函数的奇偶性周期性习题

前言

典例剖析

已知\(f(x+1)\)是周期为2的奇函数，且当\(-1\leq x\leq 0\)时，\(f(x)=-2x(x+1)\)，且\(f(-\cfrac{3}{2})\)的值为_______.

分析：由于函数\(f(x+1)\)是奇函数，故\(f(-x+1)=-f(x+1)\)，即\(f(-x+1)+f(x+1)=0\)，

故函数\(f(x)\)关于点\((1，0)\)对称，则有\(f(x)+f(2-x)=0\)，即\(f(2-x)=-f(x)\)，

又函数\(f(x+1)\)是周期函数，故\(f(x)\)也是周期为2的周期函数，

则有\(f(2-x)=f(-x)\)，故\(f(-x)=-f(x)\)，即函数\(f(x)\)为奇函数，

\(f(-\cfrac{3}{2})=-f(\cfrac{3}{2})=-f(\cfrac{3}{2}-2)=-f(-\cfrac{1}{2})=2\cdot(-\cfrac{1}{2})(-\cfrac{1}{2}+1)=-\cfrac{1}{2}\)。

【2015全国二模】已知\(f(x)\)是定义在R上的奇函数，\(f(x+1)\)是偶函数，且当\(x\in(2，4)\)时，\(f(x)=|x-3|\)，则\(f(1)+f(2)+f(3)+f(4)\)=________.

分析：由函数\(f(x+1)\)是偶函数，得到\(f(-x+1)=f(x+1)\)，

由此得到函数\(f(x)\)关于直线\(x=1\)对称，故有\(f(x)=f(2-x)\)，

又函数\(f(x)\)还是奇函数，即\(f(x)=-f(-x)\)，

这样得到\(f(2-x)=-f(-x)\)，将\(-x\)换为\(x\)，于是得到\(f(x+2)=-f(x)\)，即周期为4。

由于\(f(x)\)是定义在R上的奇函数，则有\(f(0)=0=f(4)\)，

在\(f(x)=f(2-x)\)中，令\(x=0\)得到\(f(2)=f(0)=0\)，容易得到\(f(3)=0\)，

而\(f(1)=f(-3)=-f(3)=0\)，故\(f(1)+f(2)+f(3)+f(4)=0\).

函数\(f(x)\)是周期为4的偶函数，当\(x\in[0，2]\)时，\(f(x)=x-1\)，求不等式\(x\cdot f(x)>0\)在\([-1，3]\)上的解集。

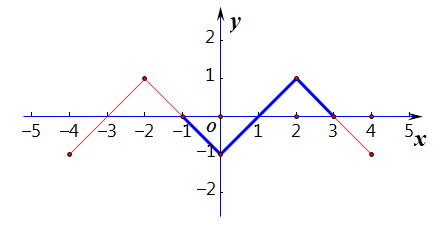
分析：自己作图，读图即可解答，解集为\((-1，0)\cup(1，3)\)；

法2：还可以利用周期和对称性求得\(f(x)\)的解析式，

代入计算，当然这个方法没有图像法直观快捷。

设\(f(x)\)是定义在R上且周期为2的函数，在区间\([-1，1]\)上，\(f(x)=\begin{cases}ax+1,&-1\leq x<0\\\cfrac{bx+2}{x+1},&0\leq x\leq 1\end{cases}\)，其中\(a,b\in R\)，若\(f(\cfrac{1}{2})=f(\cfrac{3}{2})\)，则求\(a+3b\)的值。

分析：本题目容易漏掉的一个条件是\(f(-1)=f(1)\)。

已知奇函数\(f(x)\)的定义域是\([-2,2]\)，且在区间\([-2,0]\)上递减，求满足\(f(1-m)+f(1-m^2)<0\)的实数\(m\)的取值范围。

分析：这类题目一般要考虑定义域和单调性，其中单调性的作用是去掉符号\(f\)，

①，由定义域可知，\(-2\leq 1-m\leq 2\)且\(-2\leq 1-m^2\leq 2\)

②、为去掉符号\(f\)，转化为\(f(1-m)<-f(1-m^2)\),到此还不能顺利利用单调性，

其一奇函数和在区间\([-2,0]\)上递减，得到函数\(f(x)\)在区间\([-2,2]\)上递减，

还需要利用奇函数转化为\(f(1-m)<f(m^2-1)\),这样就能利用单调性去掉符号\(f\)了，

解析：有题目可知\(\begin{cases}-2\leq 1-m\leq 2 ①\\-2\leq 1-m^2\leq 2 ②\end{cases}\)，

又函数为奇函数和在区间\([-2,0]\)上递减，得到函数\(f(x)\)在区间\([-2,2]\)上递减，

则\(f(1-m)+f(1-m^2)<0\)转化为\(f(1-m)<-f(1-m^2)=f(m^2-1)\)，

故有\(1-m>m^2-1③\)，联立①②③得到\(m\in [-1，1)\)。

【2016淄博模拟】设\(f(x)\)，\(g(x)\)分别是定义在\(R\)上的奇函数和偶函数，当\(x<0\)时，\(f'(x)g(x)\) \(+f(x)g'(x)>0\)，且\(g(-3)=0\)，则不等式\(f(x)g(x)<0\)的解集是【】

$A.(-3，0)\cup(3，+\infty)$

$B.(-3，0)\cup(0，3)$

$C.(-\infty，-3)\cup(3，+\infty)$

$D.(-\infty，-3)\cup(0，3)$

法1分析：令\(h(x)=f(x)g(x)\),则函数\(h(x)\)为奇函数，则\(h'(x)=f'(x)g(x)+f(x)g'(x)\)，

由题目可知，当\(x<0\)时，\(h'(x)>0\)，即函数\(h(x)\)在区间\((-\infty，0)\)上单调递增，

在区间\((0，+\infty)\)上单调递增，又\(g(-3)=0\)，则\(h(-3)=f(-3)g(-3)=0\)，

故在区间\((-\infty，-3)\)上\(h(x)<0\)，在区间\((-3，0)\)上\(h(x)>0\)，

\(h(0)=0\)是单独定义的，又由函数\(h(x)\)为奇函数，

故在区间\((0,3)\)上\(h(x)<0\)，\(h(3)=0\)，在区间\((3，+\infty)\)上\(h(x)>0\),

故不等式\(f(x)g(x)<0\)的解集即\(h(x)<0\)的解集为\((-\infty,-3)\cup(0,3)\)。

反思总结：注意函数\(h(x)=f(x)g(x)\)的零点有三个\(x=-3、x=0、x=3\)，

本题目容易错误的理解为在\((-\infty，0)\)单增，在\((0，+\infty)\)单增，在\(x=0\)处有定义，

那么在\((-\infty，+\infty)\)单增，这样函数\(h(x)\)的零点只有一个，这样的理解是错误的。

只有函数\(h(x)\)在\(x=0\)处左右连续，且\(\lim\limits_{x\to 0^+} h(x)=\lim\limits_{x\to 0^-} h(x)=h(0)\)，

此时的\(h(x)\)才只有一个零点。
  
法2：由上述解法可知，函数\(h(x)\)在\((-\infty，0)\)上单调递减，

在\((0，+\infty)\)上单调递增，故由\(h(x)<0=h(-3)\)，

和\(h(x)<0=h(3)\)得到，解集为\((-\infty,-3)\cup(0,3)\)。

【2017德州模拟】【单调性+奇偶性】已知函数\(f(x)\)是定义在R上的奇函数，对任意的\(x,y\in R\),\(2x+3y\neq 0\)，都有\(\frac{f(x)+f(\frac{3y}{2})}{2x+3y}<0\)，若\(2x+3y>0\)，则有【】

$A.f(2x)+f(3y)\leq 0$

$B.f(2x)+f(3y)\ge 0$

$C.f(2x)+f(3y)< 0$

$D.f(2x)+f(3y) > 0$

分析：\(\frac{f(x)+f(\frac{3y}{2})}{2x+3y}<0\)可以先变形为 \(\frac{f(x)+f(\frac{3y}{2})}{x+\frac{3y}{2}}<0\)，即\(\frac{f(x)-f(-\frac{3y}{2})}{x-(-\frac{3y}{2})}<0\)，

令\(x_1=x，x_2=-\cfrac{3y}{2}\)，则\(\cfrac{f(x_1)-f(x_2)}{x_1-x_2}<0\)，即函数\(f(x)\)为R上的减函数，

结合\(2x>-3y\),可得\(f(2x)<f(-3y)=-f(3y)\)，故有\(f(2x)+f(3y)< 0\)。故选\(C\)。

【2016\(\cdot\)成都模拟】已知函数\(f(x)\)是定义在\(R\)上的奇函数，当\(x>0\)时，\(f(x)=1-2^{-x}\)，则不等式\(f(x)<-\cfrac{1}{2}\)的解集是【】

$A.(-\infty，-1)$ $B.(-\infty，-1]$ $C.(1，+\infty)$ $D.[1，+\infty)$

法1：先求得函数\(f(x)\)的解析式，转化为分段函数不等式求解；

当\(x<0\)时，则\(-x>0\)，故\(f(x)=-f(-x)=-(1-2^x)=-1+2^x\)，

故函数\(f(x)\)的解析式为\(f(x)=\begin{cases}1-2^{-x}，&x\ge 0\\-1+2^x，&x<0\end{cases}\)，求\(f(x)<-\cfrac{1}{2}\)，

等价转化为\(\begin{cases}x\ge0\\1-2^{-x}<-\cfrac{1}{2}\end{cases}\)，或\(\begin{cases}x<0\\-1+2^x<-\cfrac{1}{2}\end{cases}\)，

解得\(x<-1\)，故选\(A\)；

法2：利用奇函数的对称性求解，由于奇函数的图像关于原点对称，

当\(x>0\)时，\(f(x)=1-2^{-x}>0\)，而\(f(x)<-\cfrac{1}{2}\)的解集和\(f(x)>\cfrac{1}{2}(x>0)\) 的解集关于原点对称，

故先求解不等式\(f(x)>\cfrac{1}{2}(x>0)\) ，

得到\(1-2^{-x}>\cfrac{1}{2}(x>0)\)，解得\(x>1\)，

故原不等式\(f(x)<-\cfrac{1}{2}\)的解集为\(x<-1\)，故选\(A\)。

已知定义在\(R\)上的偶函数\(f(x)\),在\(x\ge 0\)时，\(f(x)=e^x+ln(x+1)\)，若\(f(a)<f(a-1)\)，则\(a\)的取值范围是【】

$A.(-\infty，1)$ $B.(-\infty，\cfrac{1}{2})$ $C.(\cfrac{1}{2}，1)$ $D.(1，+\infty)$

分析.根据题中所给的函数解析式,可知函数\(y=e^x，y=ln(x+1)\)在\([0，+\infty)\)上是增加的,

故函数\(f(x)=e^x+ln(x+1)\)在\([0，+\infty)\)上是增加的,

根据偶函数图像的对称性,可知函数在\((-\infty，0]\)上是减少的,

所以\(f(a)<f(a-1)\)等价于\(|a|<|a-1|\)，两边同时平方去掉绝对值符号，

解得\(a<\cfrac{1}{2}\)，故选\(B\)。

解后反思：①、本题目如果分类讨论去掉符号\(f\)，就会变得很麻烦。②、遇到两个绝对值符号，通常平方处理。

【2019届高三理科函数的奇偶性周期性课时作业第7题】设函数\(f(x)(x\in R)\)满足\(f(x+\pi)=f(x)+sinx\)，当\(0\leq x<\pi\)时，\(f(x)=0\)，求\(f(\cfrac{23\pi}{6})\)的值。

分析：\(f(x+2\pi)=f[(x+\pi)+\pi]=f(x+\pi)+sin(x+\pi)\)

\(=[f(x)+sinx]-sinx=f(x)\)，故\(T=2\pi\)，

则\(f(\cfrac{23\pi}{6})=f(\pi+\cfrac{5\pi}{6})=f(\cfrac{5\pi}{6})+sin\cfrac{5\pi}{6}=0+\cfrac{1}{2}=\cfrac{1}{2}\)。

【2019届高三理科函数的奇偶性周期性课时作业第13题】设定义在\(R\)上的函数\(f(x)\)同时满足一下条件：

①\(f(x)+f(-x)=0\)；

②\(f(x)=f(x+2)\)；

③当\(0\leq x<1\)时，\(f(x)=2^x-1\)，

则\(f(\cfrac{1}{2})+f(1)+f(\cfrac{3}{2})+f(2)+f(\cfrac{5}{2})\)的值是_________。

分析：由①知，函数为奇函数，在利用③先做出\([0，1)\)上的图像，

再利用奇函数，做出\((-1，0]\)上的图像，一个周期基本完成，就差端点值\(f(-1)\)和\(f(1)\)的值未确定；

难点是求\(f(1)\)的值，可以通过以下几个思路求解，

法1：图像法，假设\(f(1)=\cfrac{1}{2}\)，则\(f(-1)=-\cfrac{1}{2}\)，奇偶性是说的通的，

但是周期性不满足，因为向右平移一个周期后，元素\(1\)对应\(\cfrac{1}{2}\)，还对应\(-\cfrac{1}{2}\)，

出现了一对多，不是函数了，故只能有\(f(1)=0\)，即也有\(f(-1)=0\)，

这样在一个周期上奇偶性和周期性都是满足的。

法2：题中没有明确告诉，但是由①②可知，

\(f(x+2)=-f(-x)\)，即\(f(x+2)+f(-x)=0\)，即对称中心是\((1，0)\)，

这时要么函数在\((1，0)\)处没有定义，这个不满足题意；

要么必有\(f(1)=0\)，则\(f(-1)=0\)；其余就好处理了。

法3：赋值法，由\(f(x)+f(-x)=0\)，令\(x=1\)，得到\(f(1)+f(-1)=0\)①，

令\(x=-1\)，由\(f(x)=f(x+2)\)得到，\(f(-1)=f(1)\)②，故有\(f(1)=f(-1)=0\)，

在此基础上，做出函数的大致图像，可知\(f(1)=f(2)=f(0)=0\)，

\(f(\cfrac{3}{2})+f(\cfrac{5}{2})=0\)，\(f(\cfrac{1}{2})=\sqrt{2}-1\)，

故\(f(\cfrac{1}{2})+f(1)+f(\cfrac{3}{2})+f(2)+f(\cfrac{5}{2})=\sqrt{2}-1\)。