高频易错题目 02

前情概要

• 高频易错题目01

数学概念

【2018凤翔中学高三文科冲刺模拟7第22题】【命题的真假判断】

①函数的最大值一定是函数的极大值。错，假命题。

分析：最大值可能在极大值处取到，也可能在端点处取到，而函数的极值不可能出现在端点处，一个点能否成为极值点，需要这一点的函数值和其小邻域内的其他函数值作比较，端点值不具备这一点，故端点值不能成为极值。

②函数的极大值可能会小于这个函数的极小值，正确，真命题。

分析：例如对勾函数\(f(x)=x+\cfrac{1}{x}\)，函数的极小值为\(f(1)=2\)，而函数的极大值为\(f(-1)=-2\)。

③函数在某一区间上的极小值就是函数在这一区间上的最小值。错，假命题。

分析：最小值可能在极小值处取到，也可能在端点处取到，端点处的值不能算是极值。

④函数在开区间内不存在最大值和最小值。错，假命题。

分析：正例，\(y=x\)，\(y=x^3\)，\(y=tanx\)在开区间\((-\infty，+\infty)\)上既没有最大值也没有最小值。

反例，\(y=x^2\)在开区间\((-\infty，+\infty)\)上有最小值，但没有最大值。

⑤"\(\lambda=0\)"是"\(\lambda \vec{a}=\vec{0}\)"的充分不必要条件。

分析：显然充分性成立，当\(\lambda \vec{a}=\vec{0}\)时，可能\(\lambda=0\)或者\(\vec{a}=\vec{0}\)，故必要性不成立，则命题是真命题；

⑥在\(\Delta ABC\)中，"\(AB^2+AC^2=BC^2\)"是"\(\Delta ABC\)为直角三角形"的充要条件。

分析：充分性成立，但是由直角三角形不一定能得出斜边一定为\(BC\)，故必要性不成立；故假命题；

⑦若\(a，b\in R\)，则\(a^2+b^2\neq 0\)是\(a，b\)全不为零的充要条件。

分析：由\(a^2+b^2\neq 0\)，可以得到\(a\neq 0\)或者\(b\neq 0\)，即\(a，b\)不全为零，故充分性不成立，但必要性成立；故假命题；

⑧若\(a，b\in R\)，则\(a^2+b^2\neq 0\)是\(a，b\)不全为零的充要条件。

分析：由上可知，充分性和必要性都成立，故真命题。

⑨不等式\(ax^2+bx+c\leq 0\)在\(R\)上恒成立的条件是\(a<0\)且\(\Delta \leq 0\)。

分析：由于给定不等式是仿二次不等式，故当\(a=b=0，c\leq 0\)时，不等式\(ax^2+bx+c\leq 0\)在\(R\)上也是恒成立的。故假命题。

⑩二次不等式\(ax^2+bx+c\leq 0\)在\(R\)上恒成立的条件是\(a<0\)且\(\Delta \leq 0\)。

分析：真命题。

【直线的平行和垂直】已知直线\(l_1：A_1x+B_1y+C_1=0\)，直线\(l_2：A_2x+B_2y+C_2=0\)，则\(l_1\perp l_2\Longleftrightarrow A_1A_2+B_1B_2=0\)；注意其等价条件并不是\(k_1k_2=-1\)，因为其中不包括最特殊的垂直的情形(一条直线斜率为0,而另一条直线没有斜率)；

则\(l_1// l_2\Longleftrightarrow A_1B_2-A_2B_1=0\)；注意其等价条件并不是\(\cfrac{A_1}{A_2}=\cfrac{B_1}{B_2}\neq \cfrac{C_1}{C_2}\)；

例如，直线\((m+3)x+my-2=0\)和直线 \(mx-6y+5=0\)互相垂直，求\(m\)的值。

分析：由\((m+3)m-6m=0\)解得，\(m=0\)或\(m=3\)；

例如，直线\(ax+y=1\)和直线\(9x+ay=1\)互相平行，求\(m\)的值。

分析：由\(a^2-9=0\)解得，\(a=-3\)或\(a=3\)；

关于\(x\)的不等式\(\cfrac{ax-5}{x-a}<0\)的解集是\(M\)，若\(3\in M\)且\(5\notin M\)，求实数\(a\)的范围；

分析：\(3\in M\)对应于\(\cfrac{3a-5}{3-a}<0\)，

\(5\notin M\)对应与两种情形：不等式分母为零\(5-a=0\)和\(\cfrac{5a-5}{5-a}\ge 0\)，

故需要求解\(\left\{\begin{array}{l}{\cfrac{3a-5}{3-a}<0}\\{5-a=0}\end{array}\right.①\)和

\(\left\{\begin{array}{l}{\cfrac{3a-5}{3-a}<0}\\{\cfrac{5a-5}{5-a}\ge 0}\end{array}\right.②\)

解①得到\(a=5\)，

解②得到\(\left\{\begin{array}{l}{\cfrac{5}{3}<a<3}\\{1\leq a<5}\end{array}\right.\)，

即\(\cfrac{5}{3}<a<3\)

综上可知实数\(a\)的范围为\(\cfrac{5}{3}<a<3或a=5\)。

【缺少检验出错】

已知幂函数\(f(x)=x^{m^2-2m-3}(m\in N^*)\)的图像关于\(y\)轴对称，且在\((0，+\infty)\)上是减函数，则\(m\)的值是多少？

分析：由于幂函数\(f(x)\)在\((0，+\infty)\)上是减函数，则\(m^2-2m-3<0\)，解得\(-1<m<3\)，又\(m\in N^*\)，所以\(m=1\)或\(m=2\)。

又由于图像关于\(y\)轴对称，所以\(m^2-2m-3<0\)为偶数，当\(m=2\)时\(m^2-2m-3\)为奇数，舍去\(m=2\)，故\(m=1\)。

【存在单调递增区间】若函数\(f(x)=-\cfrac{1}{3}x^3+ x^2+2ax\)在\([\cfrac{2}{3}，+\infty)\)上存在单调递增区间，则实数\(a\)的取值范围是__________.

法1：由于函数\(f(x)\)在\([\cfrac{2}{3}，+\infty)\)上存在单调递增区间，

说明在此区间上，\(f'(x)> 0\)在\([\cfrac{2}{3}，+\infty)\)上能成立，

即\(f'(x)=-x^2+x+2a> 0\)在\([\cfrac{2}{3}，+\infty)\)上能成立，

即\(2a> x^2-x=(x-\cfrac{1}{2})^2-\cfrac{1}{4}=g(x)\)在\([\cfrac{2}{3}，+\infty)\)上能成立，

而函数\(g(x)_{min}=g(\cfrac{2}{3})=-\cfrac{2}{9}\)，

故\(2a> -\cfrac{2}{9}\)，即\(a> -\cfrac{1}{9}\)，

反思总结：本题目若转化为\(f'(x)\ge 0\)在\([\cfrac{2}{3}，+\infty)\)上能成立，则最后参数的值会多出\(a=-\cfrac{1}{9}\)，

若是\(f'(x)\ge 0\)，则当\(f'(\cfrac{2}{3})=0\)时，由于\(f'(x)=-(x-\cfrac{1}{2})^2+2a+\cfrac{1}{4}\)在\([\cfrac{2}{3}，+\infty)\)上单调递减，

则\(f'(x)\leq 0\)，故此时必然不存在单调递增区间，故不符合题意，所以务必要注意转化的等价性。

解后反思： 函数\(f(x)\)在区间\([m，n]\)上为增函数，则\(f'(x)\ge 0\)在区间\([m，n]\)上恒成立，且函数\(f'(x)\)不恒为零；函数\(f(x)\)在区间\([m，n]\)上存在单调递减区间，则\(f'(x)<0\)能成立，而不是\(f'(x)\leq 0\)能成立；函数\(f(x)\)在区间\([m，n]\)上存在单调递增区间，则\(f'(x)>0\)能成立，而不是\(f'(x)\ge 0\)能成立。

法2：由于函数\(f(x)\)在\([\cfrac{2}{3}，+\infty)\)上存在单调递增区间，

说明在此区间上，\(f'(x)> 0\)在\([\cfrac{2}{3}，+\infty)\)上能成立，

即\(f'(x)=-x^2+x+2a> 0\)在\([\cfrac{2}{3}，+\infty)\)上能成立，

\(f′(x)=-x^2+x+2a=-(x-\cfrac{1}{2})^2+\cfrac{1}{4}+2a\)，

当\(x\in [\cfrac{2}{3}，+\infty)\) 时，\(f′(x)_{max}=f′(\cfrac{2}{3})=\cfrac{2}{9}+2a\)。

令\(\cfrac{2}{9}+2a>0\)，

解得\(a> -\cfrac{1}{9}\)，所以\(a\)的取值范围是\((-\cfrac{1}{9}，+\infty)\)。

【存在单调递增区间】【2016 福清市级校期末】已知函数\(f(x)=lnx+(x-a)^2(a\in R)\)在区间\([\cfrac{1}{2}，2]\)上存在单调递增区间，则实数\(a\)的取值范围是多少？

分析：函数\(f(x)=lnx+(x-a)^2(a\in R)\)在区间\([\cfrac{1}{2}，2]\)上存在单调递增区间，

则函数\(f(x)\)在区间\([\cfrac{1}{2}，2]\)上存在子区间使得\(f'(x)> 0\)能成立，

\(f'(x)=\cfrac{1}{x}+2x-2a=\cfrac{2x^2-2ax+1}{x}> 0\)；

令\(h(x)=2x^2-2ax+1\) ，

法1：接上，要使\(f'(x)> 0\)能成立，则有\(h(2)> 0\) 或\(h(\cfrac{1}{2})> 0\)，

解得\(a< \cfrac{9}{4}\)，故实数\(a\)的取值范围是\((-\infty，\cfrac{9}{4})\)。

法2：正难则反，要使\(f'(x)\leq 0\)恒成立，则在区间\([\cfrac{1}{2}，2]\)上，\(h(x)\leq 0\) ，

即\(\begin{cases}h(\cfrac{1}{2})\leq 0\\h(2)\leq 0\end{cases}\)，解得\(a\ge \cfrac{9}{4}\)，

故实数\(a\)的取值范围是\((-\infty，\cfrac{9}{4})\)。

• 函数\(f(x)\)在区间\([m，n]\)上为增函数，则\(f'(x)\ge 0\)在区间\([m，n]\)上恒成立，且函数\(f'(x)\)不恒为零。

• 函数\(f(x)\)在区间\([m，n]\)上存在单调递减区间，则\(f'(x)<0\)能成立，而不是\(f'(x)\leq 0\)能成立。

【2019高三理科数学资料用题】【2018荆州模拟改编】设函数\(f(x)=\cfrac{1}{3}x^3-\cfrac{a}{2}x^2+1\)，函数\(g(x)=f(x)+2x\)，且\(g(x)\)在区间\((-2，-1)\)内存在单调递减区间，求实数\(a\)的取值范围；

分析：\(g(x)=\cfrac{1}{3}x^3-\cfrac{a}{2}x^2+1+2x\)，则\(g'(x)=x^2-ax+2\)，

由\(g(x)\)在区间\((-2，-1)\)内存在单调递减区间，得到，

\(g'(x)=x^2-ax+2<0\)在区间\((-2，-1)\)上能成立，

分离参数得到，\(a<x+\cfrac{2}{x}\)在区间\((-2，-1)\)上能成立，

而\(\left(x+\cfrac{2}{x}\right)_{max}=-2\sqrt{2}\)，当且仅当\(x=\cfrac{2}{x}\)，即\(x=-\sqrt{2}\)时取到等号，

故实数\(a\)的取值范围为\((-\infty，-2\sqrt{2})\)。

注意：存在单调递减区间，应该得到\(f'(x)<0\)能成立，而不是\(f'(x)\leq 0\)能成立。

若\(a=-2\sqrt{2}\)，由\(g'(x)=x^2+2\sqrt{2}x+2=(x+\sqrt{2})^2\ge 0\)恒成立，则函数\(g(x)\)只能有单调递增区间，不会存在单调递减区间。

【2019高三理科数学课时作业用题】数列\(a_n=f(n)\)单调递增，但函数\(y=f(x)\)不一定单调递增，但是若函数\(y=f(x)\)单调递增，则其对应的数列\(a_n=f(n)\)必然单调递增。

数列\(\{a_n\}\)单调递增的充要条件是\(a_{n+1}>a_n\)，而不是\(f'(x)\ge 0\)恒成立。题目见等差数列的例5

求解析式

若函数\(f(x)=\cfrac{x}{ax+b}(a\neq 0)\)，\(f(2)=1\)，又方程\(f(x)=x\)有唯一解，求\(f(x)\)的解析式。

法1：从数的角度分析，由\(f(2)=1\)，得到\(\cfrac{2}{2a+b}=1\)，即\(2a+b=2\)；

由\(f(x)=x\)，得到\(\cfrac{x}{ax+b}=x\)，变形得到\(x(\cfrac{1}{ax+b}-1)=0\)，

解此方程得到，\(x=0\)或\(x=\cfrac{1-b}{a}\)，又由于方程有唯一解，故\(\cfrac{1-b}{a}=0\)，

解得\(b=1\)，代入\(2a+b=2\)得到\(a=\cfrac{1}{2}\)，

再将\(x=0\)代入方程\(\cfrac{x}{ax+b}=x\)检验，发现此时要方程有意义，必须\(b\neq 0\)，

故上述的解法可能丢失了\(b=0\)的情形，当\(b=0\)时，代入\(2a+b=2\)，得到\(a=1\)，

代入验证也满足题意，故\(a=\cfrac{1}{2}\)且\(b=1\)或者\(a=1\)且\(b=0\)

综上所述，\(f(x)=\cfrac{2x}{x+2}\)或者\(f(x)=\cfrac{x}{1\cdot x+0}=1\)。

法2：从形的角度分析，图形解释如下。

已知数列\(\{lg(a_n+\cfrac{1}{2})\}\)为首项为\(lg2\)，公比为\(2\)的等比数列；求数列\(\{a_n\}\)的通项公式；

分析：\(lg(a_n+\cfrac{1}{2})=lg2\cdot 2^{n-1}=2^{n-1}\cdot lg2\)

[说明：\(2^{n-1}\cdot lg2\neq lg2^n=n\cdot lg2\)，极易出错，对数运算的级别要高于乘法运算，故先计算对数，再计算乘法]

即\(lg(a_n+\frac{1}{2})=2^{n-1}\cdot lg2=lg2^{2^{n-1}}\)[极易出错]

则\(a_n+\frac{1}{2}=2^{2^{n-1}}\)，即\(a_n=2^{2^{n-1}}-\frac{1}{2}\).

向量的夹角

若向量\(\vec{a}\)与\(\vec{b}\)的夹角\(\theta\)为钝角，则应该是\(-1<\cos\theta<0\)，而不是我们所说的\(\cos\theta<0\)，错误原因\(\cos\theta<0\)中包含了\(\theta=\pi\)，此时是平角，而不是钝角；同理，若向量\(\vec{a}\)与\(\vec{b}\)的夹角\(\theta\)为锐角，则应该是\(0<\cos\theta<1\)，而不是我们所说的\(\cos\theta>0\)，错误原因\(\cos\theta>0\)中包含了\(\theta=0\)，此时不是锐角；

同时注意，实际操作中，我们利用\(\cos\theta<0\)且\(\cos\theta\neq -1\)求解，要比求解\(-1<\cos\theta<0\)快捷的多，且不容易出错；

几何概型

如图在\(\Delta ABC\)中，\(\angle B=60^{\circ}\)，\(\angle C=45^{\circ}\)，高\(AD=\sqrt{3}\)，在\(\angle BAC\) 内作射线\(AM\)交\(BC\)于点\(M\)，则\(BM<1\)的概率是【\(\qquad\)】

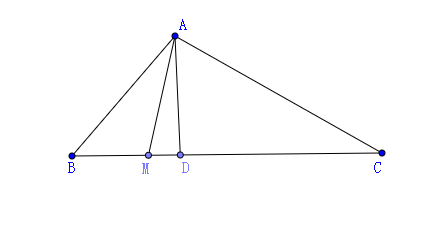
分析：本题是角度型几何概型， \(P=\cfrac{30^{\circ}}{75^{\circ}}=\cfrac{2}{5}\)。

解后反思：本例容易错误的理解为长度性几何概型， 主要是射线\(AM\)扫过\(\angle BAC\)时，用角度度量是等可能的，用长度度量不是等可能的。用课件说明：如图动画所示，当射线\(AM\)扫过\(\angle BAC\)时，我们可以看到是等速的，也就是等可能的，但是当我们看点\(M\)在线段\(BC\)上的速度时，会发现快慢不一样，即不是等速的，也就是说不是等可能的，故此时不能用线段\(BC\)的长度来度量，而应该用角度度量。

【对照题】如上图在\(\Delta ABC\)中，\(\angle B=60^{\circ}\)，\(\angle C=45^{\circ}\)，高\(AD=\sqrt{3}\)，在\(BC\)上任取一点\(M\)，则\(BM<1\)的概率是__________。

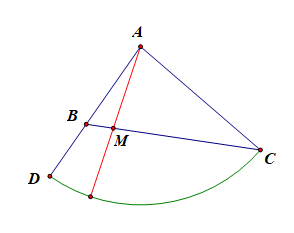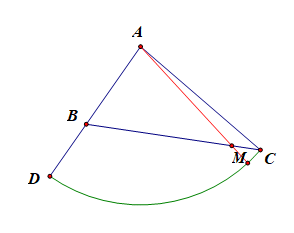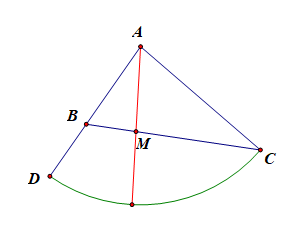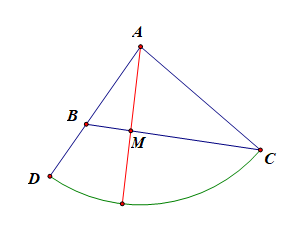
分析：本题目是长度型的几何概型，\(P=\cfrac{1}{1+\sqrt{3}}=\cfrac{\sqrt{3}-1}{2}\)。

解后反思：等可能性不是我们说等可能就能保证等可能的。

在\(\angle BAC\) 内作射线\(AM\)交\(BC\)于点\(M\)，意味着角度型；在\(BC\)上任取一点\(M\)，意味着长度型；

如图，在一个棱长为 \(2\) 的正方体鱼缸内放入一个倒置的无底圆锥形容器，圆锥的底面圆周与鱼缸的底面正方形相切，圆锥的顶点在鱼缸的缸底上，现在向鱼缸内随机地投入一粒鱼食，则“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是【\(\qquad\)】

$A.1-\cfrac{\pi}{4}$ $B.\cfrac{\pi}{12}$ $C.\cfrac{\pi}{4}$ $D.1-\cfrac{\pi}{12}$

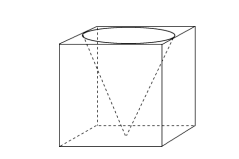
分析：选\(A\)， 本题目应该是面积型几何概型，容易错误理解为体积型几何概型；那么如何理解呢，若是体积型几何概型，则鱼食投放到鱼缸里的每一个点处都应该是等可能的，从上往下垂直投放鱼食，鱼食落在圆锥的外面正方体的下底面的中心附近的概率为零，落在下底面的顶点处的概率不为零，即不是等可能事件，故不应该是体积型几何概型。

引申：若将圆锥替换为等底的圆柱，答案应该还是 \(A\) 。