前言

• 平面的三条基本性质，也叫三条公理：

基本事实 1 ：过不在一条直线上的三个点，有且只有一个平面 .

基本事实 2 ：如果一条直线上的两个点在一个平面内，那么这条直线在这个平面内 .

基本事实 3 ：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线 .

• 平面的基本性质的推论：

推论 1 ：经过一条直线和这条直线外一点，有且只有一个平面 .

推论 2 ：经过两条相交直线，有且只有一个平面.

推论 3 ：经过两条平行直线，有且只有一个平面.

三点共线

• 证明三点共线或多点共线问题常用以下两种方法：

1、首先找出两个平面，然后证明这些点都是这两个平面的公共点，根据基本事实 3 可知，这些点都在这两个平面的交线上.

2、首先选择其中两点，确定一条直线，然后证明其余点也在这条直线上.

【人教 2019A 版教材\(P_{132}\) 页习题8.4第8题】如图，\(\triangle ABC\) 在平面 \(\alpha\) 外，\(AB\cap\alpha=P\)，\(BC\cap\alpha=Q\)，\(AC\cap\alpha=R\)，求证：\(P\)，\(Q\)，\(R\)三点共线 .

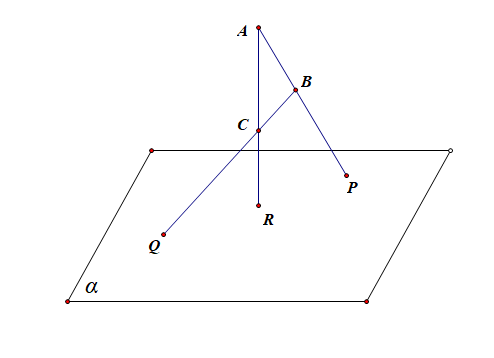
证法1：由于 \(AB\cap\alpha=P\)，\(AB\subset\) 平面 \(ABC\)，

故 点 \(P\in\)平面 \(ABC\)，又 \(P\in\alpha\)，

则 \(P\) 在平面 \(ABC\) 和平面 \(\alpha\) 的交线上，

同理可证， \(Q\) 和 \(R\) 在平面 \(ABC\) 和平面 \(\alpha\) 的交线上，

所以，\(P\)，\(Q\)，\(R\)三点共线 .

证法2：由于 \(AP\cap AR=A\)，则直线 \(AP\) 和 \(AR\) 确定平面 \(APR\)，

又由于 \(AB\cap\alpha=P\)， \(AC\cap\alpha=R\)，

则平面 \(APR\cap\alpha=PR\)，

又由于 \(B\in\) 平面 \(APR\)，\(C\in\) 平面 \(APR\)，

所以，\(BC\subset\) 平面 \(APR\)，

又由于 \(Q\in\) \(BC\)，\(Q\in\) 平面 \(APR\)，

又 \(Q\in\) \(\alpha\)，则 \(Q\in\) \(RP\)，

所以，\(P\)，\(Q\)，\(R\)三点共线 .

【人教 2019A 版教材\(P_{170}\) 页复习参考题 8 第 6 题】

三线共点

• 证明三线共点或多线共点问题的方法:

先确定待证的三线中的两条相交于一点，再证明第三条直线也过该点 . 常结合基本事实 3 ，证出该点在不重合的两个平面内，故该点在它们的交线(第三条直线)上，从而证明三线共点.

【2024高一训练题】如图，已知 \(\alpha\cap\beta=l\)，梯形 \(ABCD\) 的两底为 \(AD\)，\(BC\)，且满足 \(AB\subset\alpha\)，\(CD\subset\beta\)，求证：直线 \(AB\)，\(CD\)，\(l\) 交于一点 .

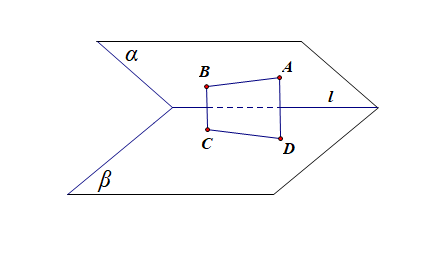
证明：由于 \(AD\)，\(BC\) 是梯形 \(ABCD\) 的两底，所以 \(AB\) 和 \(CD\) 必交于一点，设 \(AB\cap CD=M\)，

则 \(M\in AB\)， \(M\in CD\)，

又由于 \(AB\subset\alpha\)，\(CD\subset\beta\)，

则 \(M\in\alpha\)，且 \(M\in\beta\)，

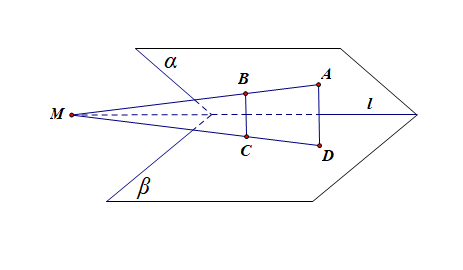
即 \(M\) 是平面 \(\alpha\) 与 \(\beta\) 的公共点，

又由于 \(\alpha\cap\beta=l\)，所以 \(M\in l\)，

即 \(AB\)，\(CD\)，\(l\) 交于一点。