球体与正四面体切接

前言

当两个非常特殊的多面体 [正四面体] 和旋转体 [球] 邂逅，又会发生什么故事呢？

正四面体与球体的切接

• 使用说明：在屏幕空白处按压鼠标左键不松手，拖动能动态观察各个角度的情况。

球体与正四面体相关计算

• 如图所示，设正四面体 \(S-ABC\) 的棱长为 \(AB=a\)，点 \(E\) 为下底面 \(ABC\) 的中心，则容易证明 \(SE\perp\) 平面 \(ABC\)，则 \(SE\) 为 正四面体的高，点 \(O\) 为 \(SE\) 的四等分点且靠近点 \(E\)，则线段 \(OE\) 为内切球的半径， 线段 \(OF\) 为棱切球的半径， 线段 \(OS\) 为外接球的半径。

① 首先从理论上说明线段 \(OE\) 为内切球的半径；

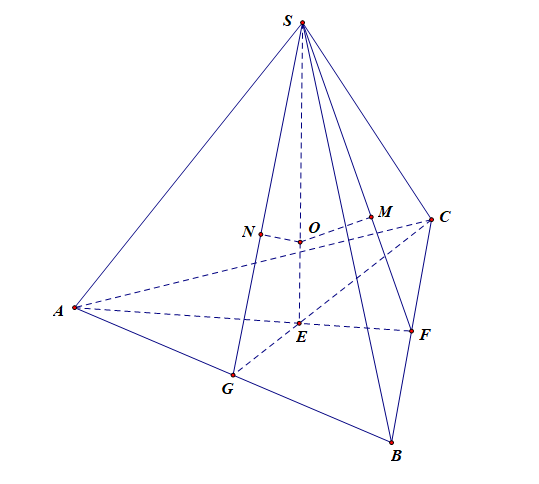
连结 \(SF\) 和 \(SG\)，过点 \(O\) 分别作 \(OM\perp SF\) 于 \(M\)， \(ON\perp SG\) 于 \(N\)，容易说明 \(OE\)，\(OM\)，\(ON\) 分别是点 \(O\) 到平面 \(ABC\)，平面 \(SBC\)，平面 \(SAB\)的距离，通过计算能得到 \(OE=OM=ON=\cfrac{\sqrt{6}}{12}a\)，同理也能计算点 \(O\) 到平面 \(SAC\) 的距离也是 \(\cfrac{\sqrt{6}}{12}a\)，故点 \(O\) 到正四面体的四个表面的距离相等，则点 \(O\) 为内切球的球心，则线段 \(OE\) 为内切球的半径；

线段 \(OF\) 为棱切球的半径，类比上法，只要计算说明 \(OF=OG\) 等；

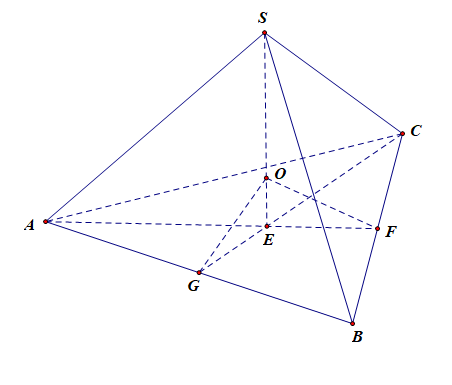
线段 \(OS\) 为外接球的半径，类比上法，只要计算说明 \(OS=OA=OB=OC\) ；

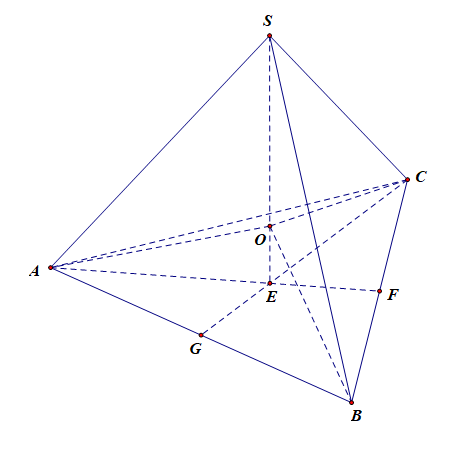
② 计算线段 \(OE\) 为内切球的半径，线段 \(OF\) 为棱切球的半径，线段 \(OS\) 为内切球的半径的长度

其高为\(h=\cfrac{\sqrt{6}a}{3}\)

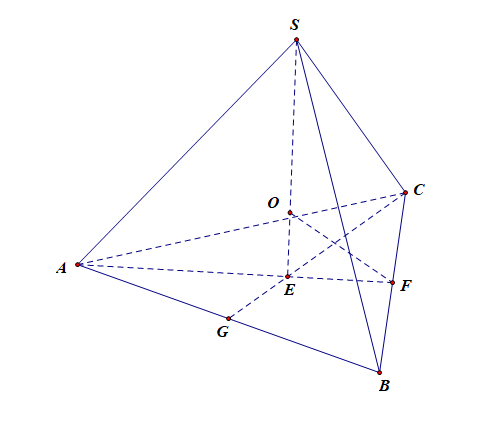
• 正四面体的内切球球心、棱切球球心、外接球球心是同一个点，在正四面体的高上，是高线上接近底面的四等分点。

• 正四面体的内切球半径\(R_{内}=\cfrac{\sqrt{6}a}{12}=\cfrac{1}{4}h=IF\)；

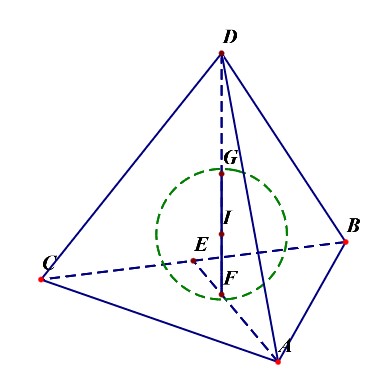
• 正四面体与各棱相切的棱切球的半径\(R_{棱}=\cfrac{\sqrt{2}a}{4}=IE\)；

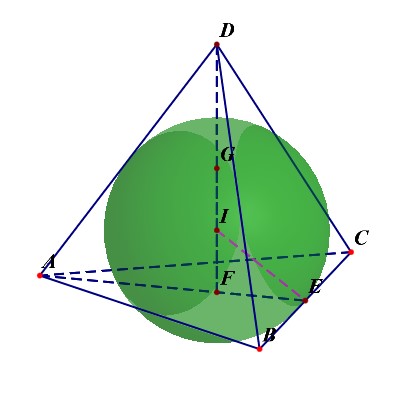
• 正四面体的外接球半径\(R_{外}=\cfrac{\sqrt{6}a}{4}=IC\)；

• 正四面体的内切球半径与外接球半径之比为\(R_{内}：R_{外}=1：3\)；\(R_{内}=\cfrac{1}{4}h\)；\(R_{外}=\cfrac{3}{4}h\)；\(h=\cfrac{\sqrt{6}}{3}a\)；

球体与正四面体转换

【2024高一训练题目】已知三棱锥 \(S-ABC\) 的所有棱长均为 \(2\)，球 \(O\) 为三棱锥 \(S-ABC\) 的外接球，则球 \(O\) 的表面积为【\(\qquad\)】

$A.\pi$ $B.2\pi$ $C.4\pi$ $D.6\pi$

解：三棱锥 \(S-ABC\) 的所有棱长均为 \(2\)，则其为正四面体，求其外接球的半径， 常考虑以下两种思路：

法1：将正四面体补体为正方体，比较容易的做法是先做出正方体，然后在其中连出来个正四面体，如图所示，

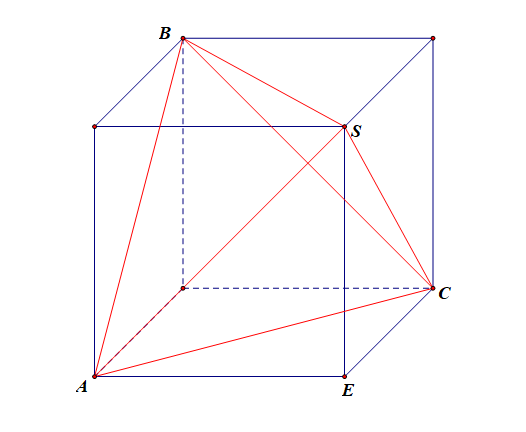
由正四面体的棱长为 \(2\)，可以求解得到正方体的棱长为 \(\sqrt{2}\)，故易得正方体的体对角线为 \(\sqrt{6}\)，故正四面体的外接球即正方体的外接球，故外接球 \(O\) 的半径为 \(R\) \(=\) \(\cfrac{\sqrt{6}}{2}\)，故 \(S_{表}\) \(=\)\(4\)\(\pi\)\(R^2\)\(=\)\(6\pi\)，故选 \(D\) .

法2：做出正四面体，如图所示，\(E\) 为点 \(S\) 在下底面的垂足且为 \(\triangle ABC\) 的重心，由于 \(AB=2\)，则 \(BF=1\)，\(AF=\sqrt{3}\)，\(AE=\cfrac{2\sqrt{3}}{3}\)，则 \(SE=\cfrac{2\sqrt{6}}{3}\)，故外接球 \(O\) 的半径为 \(R\) \(=\) \(\cfrac{3}{4}\)\(\times\)\(\cfrac{2\sqrt{6}}{3}\) \(=\) \(\cfrac{\sqrt{6}}{2}\)， 故 \(S_{表}\) \(=\)\(4\)\(\pi\)\(R^2\)\(=\)\(6\pi\)，故选 \(D\) .