Desmos 3D&Geogebra | 向量计算的工具化

前言

【2024高一数学专题训练题】在平行四边形 \(ABCD\) 中，\(AB=2BC=2\)，\(\angle DAB=60^{\circ}\)，\(E\)为\(BC\)的中点，\(F\)为\(CE\)的中点，延长 \(DF\) 交 \(BC\) 于点 \(M\) ，则 【\(\qquad\)】

$A.\quad$$\overrightarrow{DF}=\cfrac{3}{4}\overrightarrow{AB}-\cfrac{1}{4}\overrightarrow{AD}$

$B.\quad$$\overrightarrow{AC}//\bigg(\overrightarrow{EB}+\cfrac{3}{2}\overrightarrow{BM}\bigg)$

$C.\quad$$\bigg(2\overrightarrow{DF}-\cfrac{1}{2}\overrightarrow{AB}\bigg)\perp\overrightarrow{MC}$

$D.\quad\overrightarrow{AF}\cdot\overrightarrow{AM}=\cfrac{47}{12}$

参考：正确答案是 \(B\)、 \(C\)、 \(D\) .

1、前期准备：以 \(A\) 为坐标原点，以 \(AB\) 所在直线为 \(x\) 轴，以与 \(AB\) 垂直的直线为 \(y\) 轴，建立平面直角坐标系，将各点坐标化如下，

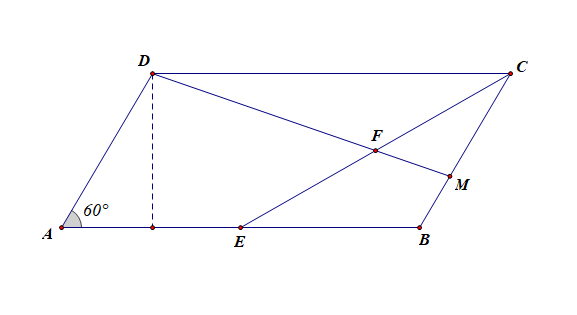
计算得到 \(A(0,0)\) ， \(B(2,0)\) ， \(C(\cfrac{5}{2},\cfrac{\sqrt{3}}{2})\) ， \(D(\cfrac{1}{2},\cfrac{\sqrt{3}}{2})\) ， \(E(1,0)\) ， \(F(\cfrac{7}{4},\cfrac{\sqrt{3}}{4})\) ， \(M(\cfrac{13}{6},\cfrac{\sqrt{3}}{6})\) ，^[1]

2、软件名称： Desmos 3D；同类型软件 Geogebra ；

3、软件地址：https://www.desmos.com/3d?lang=zh-CN

4、软件使用：

向量的输入格式，平面向量 \(v_1=((0,1),(1,2))\)，空间向量 \(v_1=((0,1),(1,2),(3,4))\)，

5、说明： 对于 \(C\) 选项，手工计算的结果是 \(\vec{V_2}\cdot\vec{V_{MC}}=0\)，但是由于浮点运算+近似计算的缘故，机器计算的结果是 \(\vec{V_2}\cdot\vec{V_{MC}}\)\(=\)\(2.7755575616\)\(\times\)\(10^{-16}\)\(\neq\)\(0\)，

Desmos 3D 计算示例

全屏

Geogebra 计算示例

---

1. 难点是求点 \(M\) 的坐标，先求 \(\overrightarrow{DF}\)，\(\overrightarrow{DF}\)\(=\)\(\overrightarrow{DC}\)\(+\)\(\overrightarrow{CF}\)\(=\)\(\overrightarrow{AB}\)\(+\)\(\cfrac{1}{2}\overrightarrow{CE}\)\(=\)\(\overrightarrow{AB}\)\(+\)\(\cfrac{1}{2}(\overrightarrow{CB}\)\(+\)\(\overrightarrow{BE})\)\(=\)\(\cfrac{3}{4}\overrightarrow{AB}\)\(-\)\(\cfrac{1}{2}\overrightarrow{AD}\)，
   设 \(\overrightarrow{BM}\)\(=\)\(\lambda\overrightarrow{BC}\)\(=\)\(\lambda\overrightarrow{AD}\)，则 \(\overrightarrow{DM}\)\(=\)\(\overrightarrow{AM}\)\(-\)\(\overrightarrow{AD}\)\(=\)\(\overrightarrow{AB}\)\(+\)\(\overrightarrow{BM}\)\(-\)\(\overrightarrow{AD}\)\(=\)\(\overrightarrow{AB}\)\(+\)\((\lambda-1)\overrightarrow{AD}\)，
   由向量 \(\overrightarrow{DF}\)、\(\overrightarrow{DM}\) 共线，则 \(\cfrac{3}{4}\times(\lambda-1)-1\times(-\cfrac{1}{2})=0\) ，解得 \(\lambda=\cfrac{1}{3}\)，
   设点 \(M(x,y)\) ，则由 \(\overrightarrow{BM}=\lambda\overrightarrow{BC}\)，得到 \((x-2,y-0)=\cfrac{1}{3}(\cfrac{5}{2}-2,\cfrac{\sqrt{3}}{2}-0)\)，解得 \(M(\cfrac{13}{6},\cfrac{\sqrt{3}}{6})\) ， ↩︎